Цели урока:
предметные – познакомиться с леммой о коллинеарных векторах и теоремой о разложении вектора по двум неколлинеарным векторам; познакомиться с понятием координаты вектора, научить находить и записывать разложение и координаты векторов способствовать формированию умений раскладывать вектор по двум данным неколлинеарным векторам;
метапредметные – понимать и использовать математические средства наглядности для иллюстрации, интерпретации, аргументации; уметь самостоятельно планировать альтернативные пути достижения целей; выстраивать аргументацию, участвовать в диалоге, приводить примеры;
личностные – иметь целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.
Задачи:
дать понятия: единичные координатные векторы, разложение вектора по единичным векторам i и j
показать образцы оформления записей;
отработать полученные знания на примерах;
контроль знаний.
Тип урока: Изучение нового материала.
Вид урока: изучение нового материала (беседа) с последующим закреплением через решение задач.
Методы и приемы обучения: объяснительно-иллюстративный; частично-поисковый; словесный (фронтальная беседа); наглядный (демонстрация компьютерной презентации); практический.
Средства обучения: авторская презентация; учебник (Л.С.Атанасян, В.Ф.Бутузова, С.Б.Кадомцева и др. Геометрия. 7-9 классы. − М.: Просвещение, 2016)[2]
технические (компьютер, мультимедийный проектор).
План урока:
1.Организационный момент. (1 минута)
2. Актуализация знаний. (4 минуты)
3. Изложение нового материала. (13 минут)
4. Физкультминутка. (3 минуты)
5. Первичное закрепление (Работа в парах)(10 минут)
6. Проверка усвоения новых знаний.(Самостоятельная работа) (10 минут)
7. Подведение итогов. (2 минуты)
8. Рефлексия (2 минуты)
9. Домашнее задание. (1минуты)
ХОД УРОКА
I. Организационный момент. ![]()
1. Приветствие.
2. Организация рабочих мест:
Нас сегодня ждет дорога,
И узнать нам надо много.
– Так возьмемся, ребята, скорей за работу!
Проверим готовность к уроку
- Проверьте ваши рабочие места: учебник, рабочая тетрадь, ручка.
Мотивационное начало урока
Сегодня на уроке мы начинаем изучение новой главы «Метод координат». Тема нашего урока – «Разложение вектора по двум неколлинеарным векторам».
Цель нашего урока – выяснить, как может быть задан вектор на координатной плоскости и научимся находить координаты вектора.
Для достижения цели нашего урока, мы воспользуемся мультимедийной презентацией.
![]()
![]() II. Актуализация знаний.
II. Актуализация знаний.
Устный опрос
1. Дайте определение вектора
[Вектором или направленным отрезком называется отрезок для которого указано, какая из его граничных точек считается началом, а какая – концом.]
2. Длина или модуль ненулевого вектора АВ – это… [длина отрезка АВ]
3. Ненулевые вектора называются коллинеарными, если… [они лежат либо на одной прямой, либо на параллельных прямых]
4. Два коллинеарных вектора направленные одинаково называются
[сонаправлеными]
5![]() . Векторы называются равными, если… [они сонаправлены и их длины равны]
. Векторы называются равными, если… [они сонаправлены и их длины равны]
Решение задач по готовым чертежам
ABCD-параллелограмм
В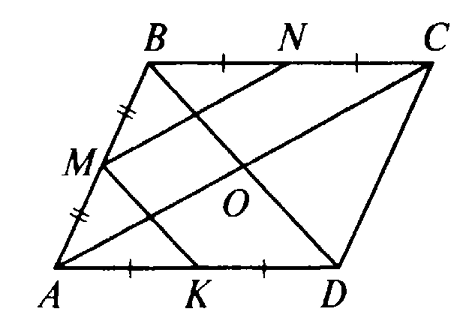 ыразите
ыразите
а) 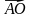 через
через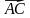
б) 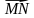 через
через 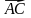 ,
, 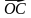
в)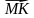 через
через 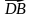 ,
, 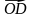
г) 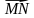 через
через 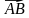 ,
, 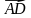
ІІІ. Изложение нового материала
– Всегда ли можно выразить один вектор через другой?
Р![]() ассмотрим два случая: 1) векторы коллинеарны 2)векторы неколлинеарны
ассмотрим два случая: 1) векторы коллинеарны 2)векторы неколлинеарны
Л![]() емма о коллинеарных векторах.
емма о коллинеарных векторах.
Работа с учебником. Разбор доказательства по учебнику. (стр. 222) [2]
В![]() вести понятие разложения одного вектора по двум неколлинеарным векторам
вести понятие разложения одного вектора по двум неколлинеарным векторам 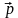 = х
= х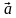 + y
+ y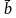 , где х, у — коэффициенты разложения.
, где х, у — коэффициенты разложения.
Теорема. Объяснение доказательства, используя учебник. (стр.223)
Ф![]()
![]() изкультминутка
изкультминутка
Н![]() арисуй глазами треугольник.
арисуй глазами треугольник.
Теперь его переверни вершиной вниз.
И вновь глазами ты по периметру веди.
Рисуй восьмерку вертикально.
Ты головою не крути,
А лишь глазами осторожно
Ты вдоль по линиям води.
И на бочок ее клади.
Теперь следи горизонтально,
И в центре ты остановись.
Зажмурься крепко, не ленись.
Глаза открываем мы, наконец.
Зарядка окончилась. Ты – молодец!
Первичное закрепление
Решение задач
Работа в парах. (Решить задачи с последующим обсуждением.)
Задача № 1
Найдите такое число q, чтобы выполнялось равенство = q
, если; а)
| |= 5 см, |
|= 2 см; б)
|
|= 0,7 м, |
|= 2 м.
Решение:
а) По условию задачи
, т.е. q 0, | q |=
= 2,5, отсюда q = 2,5
б) По условию задачи
, т.е. q | q |=
= 0,35, отсюда q = - 0,35
О твет: а) 2,5; б) -0,35.
Задача № 2.
Дано: Диагонали параллелограмма ABCD пересекаются в точке М, точка Н — середина отрезка AM.
Найдите, если это возможно, такое число k, чтобы выполнялось равенство:
а) = k
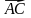 ; б)
; б) = k
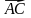 ; в)
; в) = k
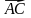 .
.
Решение:
а)
, поэтому искомое число k существует, |k| =
и k 0. Так как диагонали параллелограмма точкой М делятся пополам, то |k| =
.Итак, k =
.
б)
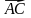 , поэтому искомое число k отрицательно |k| =
, поэтому искомое число k отрицательно |k| = и k H – середина отрезка AM, тогда МН =
АМ =
(АС:2) =
АС, поэтому |k| =
. Итак, k = -
.
в) Векторы и
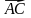 не коллинеарны, поэтому искомого значения к не существует.
не коллинеарны, поэтому искомого значения к не существует.
Ответ: а) k = , б) k = -
, в) не существует.
П ![]() роверка усвоения новых знаний
роверка усвоения новых знаний
С![]() амостоятельное решение задач.
амостоятельное решение задач.
Решить задачи № 3, № 912, 914 (а) (учебник). [2]
З адача № 3
Дано: В параллелограмме ABCD МК || DC и РТ ||DA.
Разложите по векторам 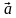 =
= ,
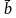 =
= векторы:
а) б)
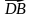
2) Разложите вектор по векторам:
а) =
,
=
; б)
=
,
=
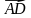 .
.
Решение:
По условию задачи МК || DC, поэтому ВОК =
ВDС. В треугольниках ВОК и ВDС угол В общий,
ВОК =
ВDС, следовательно,
ВОК
ВDС. Так как ВО =
BD,то ВК =
ВС, следовательно, точка К – середина стороны параллелограмма. Аналогично точки М, Р и Т – середины сторон данного параллелограмма.
а) По правилу параллелограмма =
+
, но
=
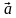 ,
, =
=
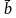 . Итак,
. Итак, =
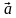 +
+
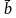 .
.
б) 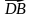 =
= +
= 2
+
= 2
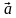 +
+ 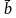 .
.
2) a) По правилу параллелограмма =
+
=
+
=
+
б) =
+
=
+ (-
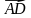 ) =
) = -
.
О![]() твет: 1) а)
твет: 1) а) =
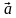 +
+
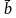 ; б)
; б) 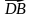 = 2
= 2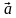 +
+ 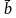 . 2) а)
. 2) а) =
+
; б)
=
-
.
Подведение итогов.
1. Всегда ли можно выразить один вектор через другой?
2. Сформулируйте лемму о коллинеарных векторах.
3. Что значит «разложить вектор по двум неколлинеарным векторам»?
4. Как называются числа х и у в записи 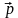 = х
= х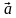 + у
+ у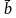
5. Сформулируйте теорему о разложении вектора по двум неколлинеарным векторам.
VIII. Рефлексия.
У![]() чащимся предлагается назвать три момента, которые у них получились хорошо в процессе урока, и предложить одно действие, которое улучшит их работу на следующем уроке.
чащимся предлагается назвать три момента, которые у них получились хорошо в процессе урока, и предложить одно действие, которое улучшит их работу на следующем уроке.
I X. Домашнее задание
1. П. 89 (разобрать доказательство леммы о коллинеарных векторах), вопросы 1 - 3 (учебник, с. 244). [2]
2. Решить задачи № 911, 914 (б, в), 915 (учебник).

 Получите свидетельство
Получите свидетельство Вход
Вход












 Конспект урока "Разложение вектора по двум неколлинеарным векторам" (158.41 KB)
Конспект урока "Разложение вектора по двум неколлинеарным векторам" (158.41 KB)
 0
0 708
708 157
157 Нравится
0
Нравится
0


