Конспект урока «Прямоугольный параллелепипед»

ОТКРЫТЫЙ УРОК ПО ТЕМЕ:

« ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД»

На доске записана тема урока «Прямоугольный параллелепипед»

Цели урока:

1) образовательные: развитие исследовательских навыков, ввести понятие прямоугольного параллелепипеда, рассмотреть свойства прямоугольного параллелепипеда, показать их применение при решении задач.

2) развивающие: уметь самостоятельно делать выводы, развивать математическую речь и логику учащихся.

3) воспитательные: воспитывать аккуратность в построении пространственных фигур, умение работать в группе, помогать товарищу, воспитывать коммуникативные умения и навыки, адекватную самооценку.

Тип урока: урок изучения нового материала.

Методы: частично-поисковый.

Формы организации деятельности учащихся: фронтальная, индивидуальная,

работа в парах, индивидуальная самостоятельная работа, тест.

Оборудование: мультимедийный проектор, девиз урока, готовые чертежи, модели цветных прямоугольных параллелепипедов, линейка, задачи и домашнее задание на карточках, логическая задача на листе формата А₄.

Организационный момент

Ученики мои! Я очень рада

Войти в приветливый ваш класс

И для меня уже награда

Вниманье ваших умных глаз.

Девиз нашего урока: «Лучший способ изучить что-либо – это открыть самому»

(Дьёрдь Пойа - венгерский, швейцарский и американский математик)

На уроках геометрии очень важно уметь смотреть и видеть, замечать и отмечать различные особенности геометрических фигур.

Кто ничего не замечает

Тот ничего не изучает

Кто ничего не изучает

Тот вечно хнычет и скучает.

Актуализация знаний учащихся.

 Сегодня мы с вами на уроке будем говорить о параллелепипеде, поэтому вспомним:

II. Фронтальный опрос:

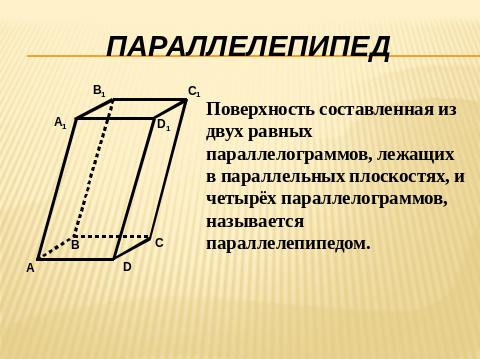(Слайд 4)

- Какая поверхность называется параллелепипедом? (Поверхность составленная из двух равных параллелограммов, лежащих в параллельных плоскостях, и четырёх параллелограммов, называется параллелепипедом.)

- Как называются параллелограммы, из которых составлен параллелепипед? (Параллелограммы, из которых составлен параллелепипед, называются гранями. )

- Какие грани называются основаниями, боковыми гранями? (Две противоположные грани называются основаниями, остальные - боковыми)

- Что можно сказать о противоположных гранях параллелепипеда? (Противоположные грани параллелепипеда параллельны и равны)

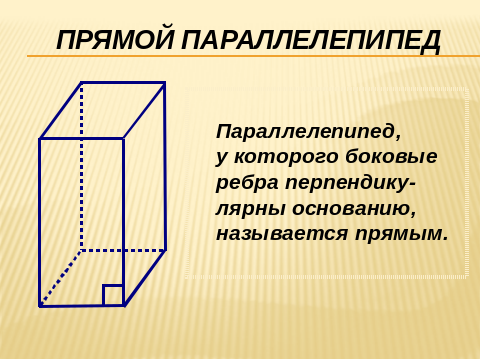(Слайд 5)

- Какой параллелепипед называется прямым? (параллелепипед называется прямым, если боковые рёбра перпендикулярны основанию)

III. Изучение нового материала:

Работаем в паре. У Вас на столе стоит геометрическая фигура. Является ли она прямым параллелепипедом? (да)

Выделите основания параллелепипеда, определите вид четырёхугольника. Как он называется? (Прямоугольник)

Параллелепипед, у которого боковые рёбра перпендикулярны к основанию, а основания представляют собой прямоугольники, называется прямоугольным. Теперь мы знаем все виды параллелепипедов.

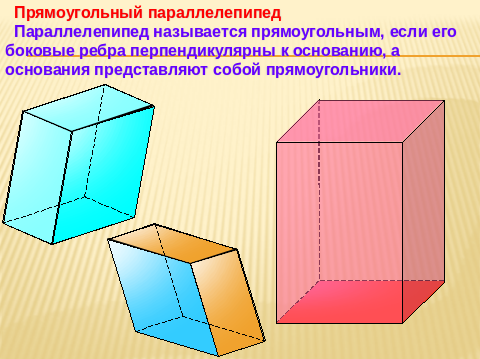(Слайд 6)

Записываем тему нашего урока «Прямоугольный параллелепипед». (Слайд 7)

Посмотрите на грани вашего параллелепипеда.

- Сколько граней у параллелепипеда? (6)

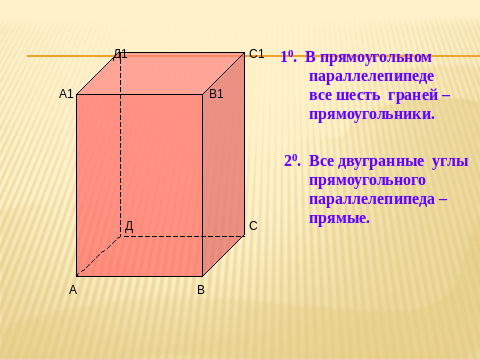(Слайд 8)

Про основания мы уже сказали, что они – прямоугольники, а боковые грани какой вид четырёхугольника имеют? (прямоугольники)

(Записываем ) Свойство 1. В прямоугольном параллелепипеде все шесть граней прямоугольники.

- Как называются две грани параллелепипеда, имеющие общее ребро?(две грани параллелепипеда, имеющие общее ребро, называется смежными)

Назовите смежные грани. ( АВВ₁ и АВС). Докажите, что смежные грани перпендикулярны. (Боковые рёбра перпендикулярны основанию, а через ребро проходит грань, тогда по признаку перпендикулярности двух плоскостей: Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны)

(Записываем ) Свойство 2. Все двугранные углы прямоугольного параллелепипеда – прямые.

(Назовите хотя бы один двугранный угол прямоугольного параллелепипеда)

- Сколько рёбер имеет параллелепипед? (12)

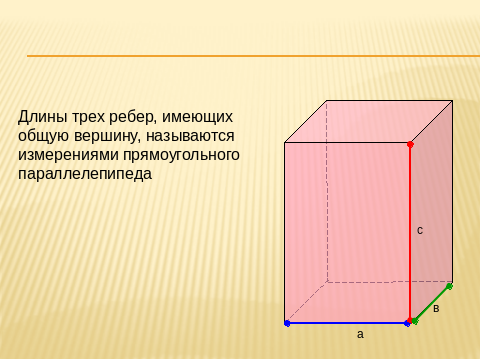(Слайд 9)

Длины трёх рёбер, имеющих общую вершину, называются измерениями прямоугольного параллелепипеда.

Классная комната является прямоугольным параллелепипедом. В обыденной практике, говоря о размерах комнаты, мы используем слова «длина, ширина, высота»

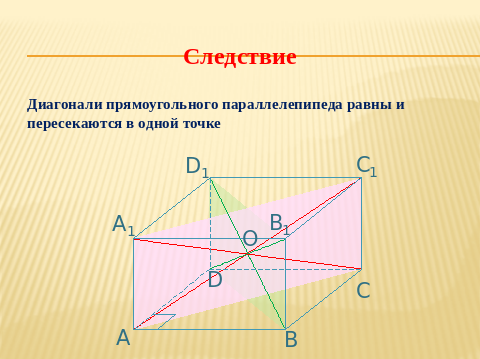
- Как называется отрезок, соединяющий противоположные вершины параллелепипеда? (отрезок, соединяющий противоположные вершины параллелепипеда, называется диагональю).

Сравнение планиметрии и стереометрии.

Вспомним чему равен квадрат диагонали прямоугольника? (квадрат диагонали прямоугольника равен сумме квадратов двух его измерений)

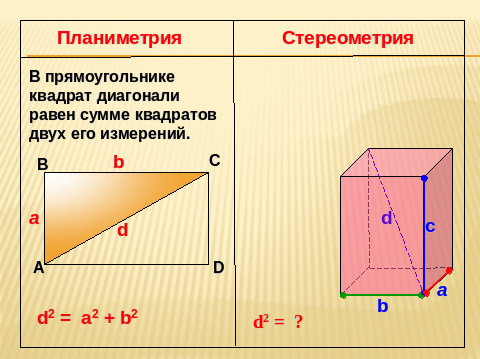(Слайд 10)

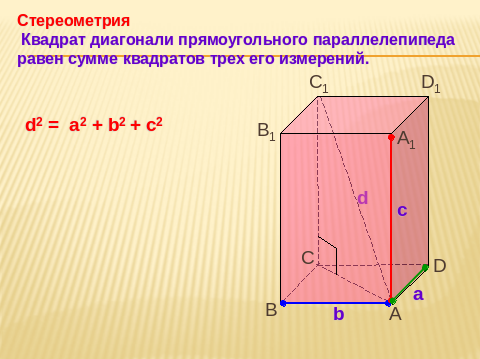
Решим задачу (рис.1) Дано: АВ= а, ВС= в, ВВ1= с. Найти диагональ ВД1(d).

1. Решает ученик на доске. Из ∆ BDD₁ прямоугольного, BD₁² = BD²+ DD₁²

2. Из АВDС прямоугольника, АD² = AВ²+ АD²

3. Из 1 и 2 следует BD₁² = ВС²+ АВ² + СС₁²

4. d² = a²+ b² + c²

Вывод: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Мы доказали свойство прямоугольного параллелепипеда связанное с его измерениями: (Слайд 12)

- Сколько диагоналей имеет параллелепипед? (4)

(Слайд 13)

Практическое задание. (На столах раздаточный материал – прямоугольные параллелепипеды)

Работаем в паре. Измерьте длину, ширину, высоту прямоугольного параллелепипеда. Вычислите длину диагонали прямоугольного параллелепипеда.

Самопроверка по образцу (на столах под прямоугольным параллелепипедом карточка с решением).

Устная работа по готовым чертежам

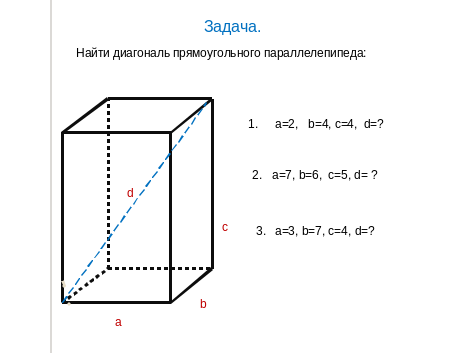
1 . d = 6 2. d = √110 3. d =

Физкультминутка.

Кабинет, в котором мы занимаемся, имеет форму параллелепипеда. Покажите переднюю грань, верхнее основание, боковые грани, нижнее основание, диагонали.

Формирование умений и навыков:

1. Письменно:

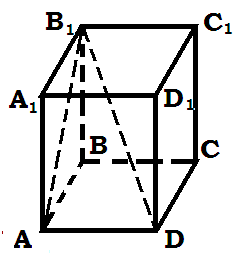Дано: ABCDA₁B₁C₁D_{1 -} прямоугольный параллелепипед, DC=8см,

АD=9см, DD₁=12 см

Найдите: диагональ DB₁ параллелепипеда и синус угла между диагональю параллелепипеда и плоскостью AA₁B_1.

Решение: DB_{1= √ 144+81+64 = 17}

sin DB₁A= 9

Дифференцированная самостоятельная работа:

Приложение 1

Дифференцированная самостоятельная работа:

Вариант I. ФИ__________________________________

Уровень I.

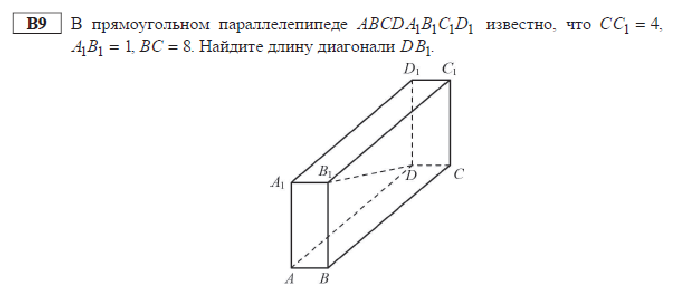
1. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известно, что СС₁=4, АВ=1, В₁С₁=8. Найти длину диагонали DB₁.

Решение:

Уровень II.

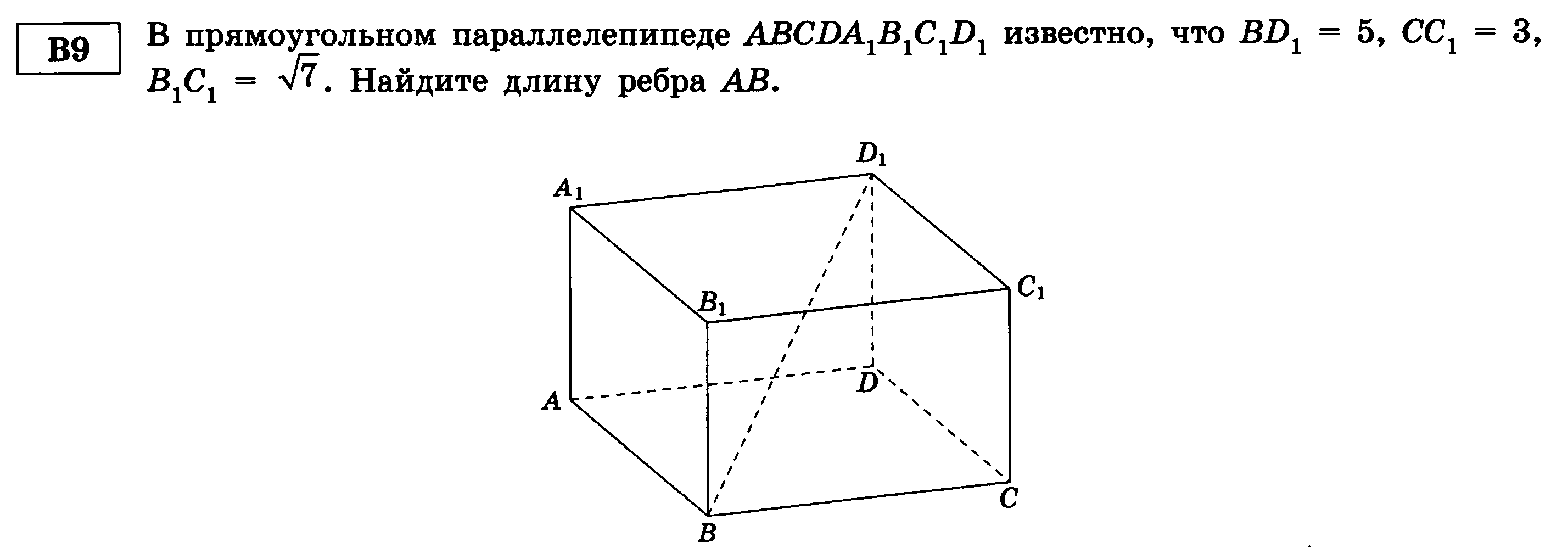
1. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известно, что BD₁=5, DD₁=3, ВС=√7. Найти длину ребра АВ.

Решение:

Уровень III.

1. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известно, что BD₁=5, CC₁=3, В₁С₁=√7. Найти синус угла между DB₁ и плоскостью основания.

Решение:

Дифференцированная самостоятельная работа:

Вариант II. ФИ__________________________________

Уровень I.

1. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известно, что СС₁=5, АВ=1, В₁С₁=10. Найти длину диагонали DB₁.

Решение:

Уровень II.

2.В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известно, что BD₁=5, DD₁=3, ВС =√7. Найти длину ребра АВ.

Решение:

Уровень III.

3.В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известно, что BD₁=7, СС₁=4,

В₁С₁=√1 0. Найти косинус угла между DB₁ и плоскостью основания.

Решение:

1. Устно: № 188

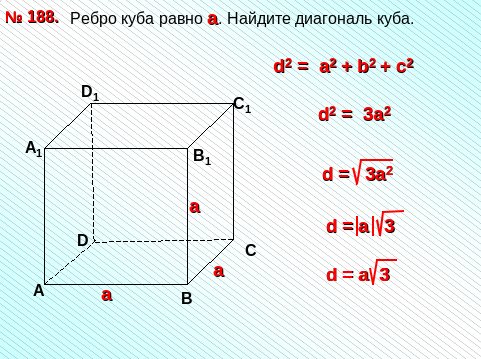
(Письменно решает весь класс, один ученик на доске)

№ 189. Найдите расстояние от вершины куба до плоскости любой грани, в которой не лежит эта вершина, если: б) диагональ куба равна d.

Тест. (Взаимопроверка, Одна ошибка – «4», две- «3» )

Верны ли следующие утверждения:

1. Треугольник являться гранью прямоугольного параллелепипеда.

2. У прямоугольного параллелепипеда три пары равных граней.

3. Отрезок соединяющий противоположные вершины грани называется диагональю прямоугольного параллелепипеда.

4. В прямоугольном параллелепипеде два измерения.

5.Может ли гранью параллелепипеда являться квадрат?

Ответ: Нет, Да, Нет, Нет, Да

(Запись учащихся должна быть такой: _ V _ _V)

Рефлексия: (Электронный тест ЭОР)

- Какой параллелепипед считается прямоугольным.

- Какими свойствами обладает прямоугольный параллелепипед.

Домашнее задание: п. 24 Прямоугольный параллелепипед. Выучить определение, свойства. Письменная работа на карточках.

№ ___________________

Приложение 2

Практическая работа

Измерьте длину, ширину, высоту прямоугольного параллелепипеда. Найдите длину диагонали.

№1 а=3, в=5, с=9 d=√9+25+81= √115

№ 2 а=6, в=3, с=12 d=√36+9+144= √189

№ 3 а=6, в=4, с=15 d=√36+16+225= √277

№ 4 а=5, в=8, с=15 d=√25+64+225= √314

№ 5 а=5, в=5, с=11 d=√25+25+121= √171

№ 6 а=6, в=4,5, с=14 d=√36+20,25+196= √252,25

№ 7 а=6, в=4,5, с=11 d=√36+20,25+121= √177,25

№ 8 а=2,5, в=2,5, с=5,5 d=√6,25+6,25+30,25= √42,75

Приложение 3

Домашняя письменная работа по теме «Прямоугольный параллелепипед и его свойства»

1 Вариант

1. Найдите квадрат расстояния между вершинами B и D₁ прямоугольного параллелепипеда, для которого AB=4, AD=6, AA₁=5

2. Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого AB=6, AD=8, AA₁=3

3. Найдите расстояние между вершинами B и A₁ прямоугольного параллелепипеда, для которого AB=12, AD=7, AA₁=5

2 Вариант

1. Найдите расстояние между вершинами B и D прямоугольного параллелепипеда, для которого AB=5, AD=12, AA₁=5

2. Найдите квадрат расстояния между вершинами D и B₁ прямоугольного параллелепипеда, для которого AB=7, AD=7, AA₁=4

3. Найдите расстояние между вершинами A₁ и D прямоугольного параллелепипеда, для которого AB=4, AD=12, AA₁=9

Заполните таблицу:

Заполните таблицу: