Конспект урока-практики по теме "Площади плоских фигур. Воплощаем в жизнь"

МБОУ Трыковская СОШ

Итоговый урок-практимум по геометрии

по теме «Площади плоских фигур»

Разработала и провела

учитель математики 1 категории

МБОУ Трыковская СОШ

Жилина Оксана Леонидовна

2018-2019 учебный год

Урок-практикум  «Геометрия в профессии дизайнера» в 8 классе

Тема урока: Площади плоских фигур.

Тип урока: повторительно-обобщающий.

Цели и задачи урока:

Учебные:

• проверить и систематизировать знания учащихся по данной теме

• закрепить умения учащихся применять формулы нахождения площадей фигур при решении задач

Развивающие:

• развитие у учащихся самостоятельности и способности к самоорганизации;

• формирование навыка исследовательской деятельности;

• повышение уровня математической культуры учащихся.

Воспитательные:

• воспитывать толерантность и умение работать в парах, группе.

Планируемые результаты:

личностные:

умение понимать смысл поставленной задачи, ясно и чётко излагать свои мысли в устной речи, выстраивать аргументацию, приводить контрпримеры;

опыт смыслообразования;

самооценка результатов деятельности, осознание границ применения нового знания;

умение работать в команде;

ценностно-эмоциональное отношение к изучаемому математическому содержанию с общекультурных позиций;

представление о значении математической науки как сфере человеческой деятельности;

метапредметные:

умение выделять главное, сравнивать, обобщать, проводить аналогию, применять индуктивные способы рассуждений, выдвигать гипотезы при решении учебных задач;

осознанное чтение текста;

способность к интерпретации;

представление о математике как средстве моделирования явлений окружающего мира;

предметные:

понятие площади фигур;

умение использовать формул для вычисления площадей плоских фигур и строить речевые высказывания с использованием специальной терминологии;

умение устанавливать закономерность в применении формул;

умение изображать геометрические фигуры;

использовать различные языки математики (словесный – символический – графический).

Структура урока:

1. Организационный момент.

2. Устная работа с классом.

3. Письменное решение заданий из ОГЭ и ЕГЭ.

4.  Решение задач прикладного характера (игра «Дизайнер», «Мозаика»)

5.  Итог урока.

6.  Домашнее задание.

Ход урока:

1. Организационный момент. Сообщение темы урока.

Ребята, сегодняшний урок мы посвятим решению задач на вычисление площадей плоских фигур. Но задачи, которые мы будем решать на уроке отличаются от ранее рассмотренных, так как они встречаются в окружающей нас действительности, решать их нас «заставляет» сама жизнь. Они встречаются в различных областях человеческой деятельности, их решают люди разных профессий.

Эпиграфом к нашему уроку я взяла слова А.Н. Колмогорова «Знания по геометрии или умение пользоваться формулами необходимы почти каждому мастеру или рабочему».

Как вы думаете, какова цель нашего урока?

Данный урок – это урок систематизации и обобщения полученных знаний и применения этих знаний на практике. Разнообразные задания разного уровня позволят активизировать вашу мыслительную деятельность, развивать логику и мышление, способствовать воспитанию интереса к предмету, научат анализировать, обобщать и рассуждать, а также они направлены на развитие творческих способностей.

II. Проверка знаний учащихся.

1. Проведем самостоятельную работу по проверке теории. У каждого на столе есть таблицы с названием, изображением фигур и формулами для вычисления их площадей. Задание: составить соответствие фигуры и формулы.

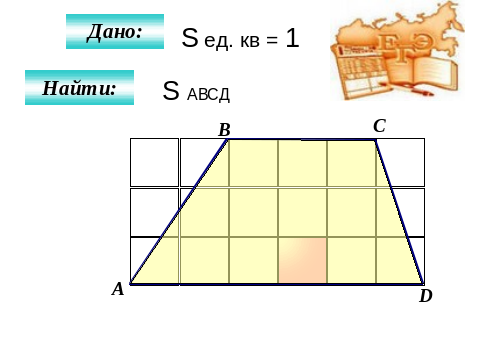
2. Решите задачи по готовым чертежам (СМ. приложение: задачи из сборников ОГЭ -2019 и ЕГЭ-2019)

Физминутка. Мы немного отвлечёмся и гимнастикой займемся – глазками вращая за движением фигур дружно наблюдаем. Немного размялись – пора снова в путь.

III. Геометрия в профессии дизайнера

Ребята, знание геометрии необходимо в различных областях человеческой деятельности. Формулы площадей плоских фигур нам приходится повторять на протяжении всей жизни. И сегодня мы рассмотрим значение геометрии в профессии дизайнера.

Дизайнер. Это слово вошло в русский язык несколько десятилетий назад. В английском языке designer – проектировщик, создатель оригинальных эскизов, образов, моделей, узоров.

Как вы думаете, кто такой дизайнер?

- Дизайнер – это специалист, имеющий художественное образование.

Что входит в сферу деятельности дизайнера?

- В сферу деятельности дизайнера входит дизайн одежды, обуви, мебели, ткани, дизайн рекламы, ландшафтный дизайн, архитектурный дизайн.

1). Полиграфический дизайн (Красочное и яркое оформление визиток, открыток, буклетов)

2) Ландшафтный дизайн (оформление садов, парков, клумб)

3). Дизайн интерьера (оформление помещения, комнаты).

4). Стилист (оформление внешнего облика человека, формирование стиля).

В настоящее время наиболее востребованы дизайнеры, работающие в области полиграфии, а также дизайнеры по интерьеру.

А сейчас мы поиграем в игру «Дизайнер».

1. Представьте, что вы дизайнер интерьера. Поступил заказ «Подсчитать сколько краски потребуется для покраски стен комнаты, если её размеры 6 х 8 х 3 м, при этом учтите, что есть дверь размером 2 х 0,8, три окна размерами 2 м х 2 м и шкаф размером 1,5х2м (на 1кв.м. расходуется 200 г краски)?

Сколько плиток паркета 0,5м х 0,5м нужно купить для пола?»

2. Игра «Мозаика» (Д/з было придумать узор из мазайки)

Сколько стекла потребуется для создания такой мозаики? Размеры стекла в двери 2×1 м.

1 группа) зелёного цвета

2 группа) красного цвета

3 группа) желтого цвета

3. Индивидуальная работа. Письменное задание всем, два человека у доски: «Рассчитай количество необходимых денежных  средств для покупки линолеума»

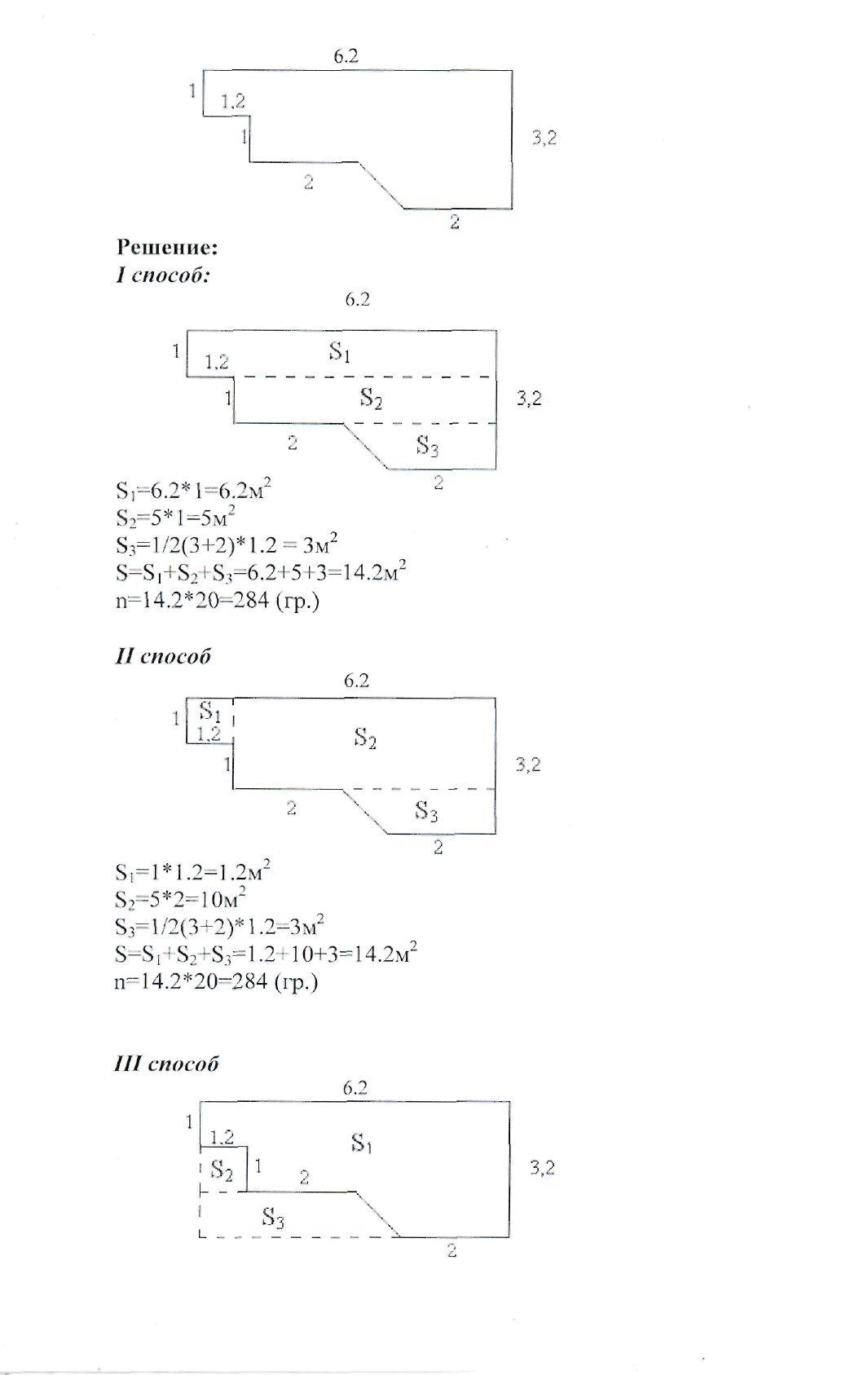
7. У каждого ученика имеется конструктор из 8 равнобедренных прямоугольных треугольников, катет которых равен 4 см. Построить, найти площадь и рассказать о применении фигур:

1) Квадрат, площадь которого 16 см²

Квадрат, площадь которого 64 см²

решение

S = a²

S = 4² = 16(см²)

S = 8х8 = 64(см²)

Определение квадрата. Как найти его площадь?

Определение прямоугольного треугольника. Как найти его площадь?

2) Ромб, площадь которого 32 см²

решение

,

Определение ромба. Два способа вычисления его площади?

3) Прямоугольник, площадь которого 32 см²

решение

S = 4х8=32(см²)

Определение прямоугольника. Как найти его площадь?

IV. Итог урока

Как вы считаете, актуальны ли в наше время слова Андрея Николаевича Колмогорова: «Знания по геометрии или умение пользоваться формулами необходимы почти каждому мастеру или рабочему».

- Да актуальны. На уроке мы узнали, что знания геометрии необходимы современному человеку, без геометрических знаний не может обойтись ни архитектор, ни дизайнер, ни художник, ни строитель.

- Формулы площадей плоских фигур нам придется повторять на протяжении всей жизни: при ремонте дома, планировке, вычислении земельных угодий, посеве и уборке урожая, в производительном труде.

Сегодня на уроке мы с вами создали производ­ственную ситуацию, в которой вы поставили себя на место дизайнера, я думаю, что вы смогли увидеть и оценить значение математических знаний в производительном труде, научились само­стоятельно при­менять полученные знания на практике.

Оценка знаний: Оценки за выполненную работу выставляются с учетом вклада каждого ученика и количества допущенных ошибок.

V. Домашнее задание. Творческая работа.

1. Подсчитать, какая сумма денег необходима для ремонта комнаты

(данные для расчетов взять в магазине, Интернете, спросить у родителей и т.д.).

1. Придумать и нарисовать в тетради свой рисунок  мозаики для стеклянной двери. Рассчитать количество необходимого материала.

2. Написать мини-сочинение «Для чего изучаем геометрию мы?» Предлагаю начать со слов: «Греки изучали её, чтобы познать мир, а римляне – для того, чтобы измерять земельные участки».

VI. Рефлексия

Я на время представила себя полиграфическим дизайнером и подготовила вам буклеты «Плоские фигуры», чтобы вы смело могли применять знания на практике. Удачи вам! Спасибо за урок!

Приложение.

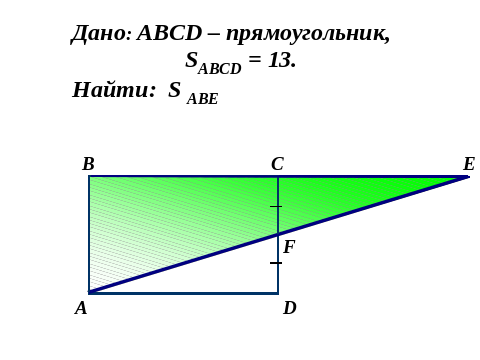
В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45⁰ . Найдите площадь треугольника.

А

В С

10

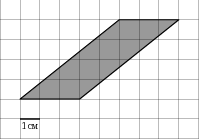
На клетчатой бумаге с клетками размером 1 см х 1 см изображен параллелограмм. Найдите его площадь в квадратных сантиметрах.

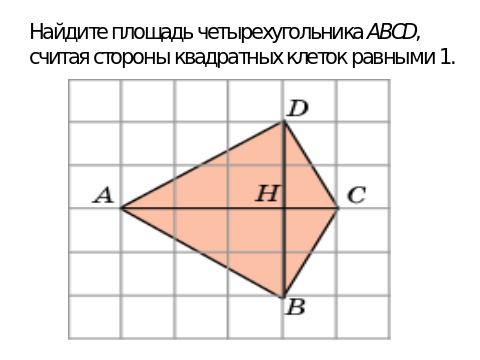
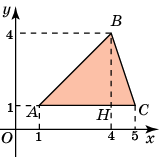
Найдите площадь треугольника, вершины которого имеют координаты (1, 1), (4, 4), (5, 1).