Муниципальное бюджетное общеобразовательное учреждение-центр образования №8 город Тула
Работа подготовлена на конкурс методических разработок «Инновационные технологии при обучении математике»
Конспект урока геометрии в 11 классе
по теме
« Цилиндр. Площадь поверхности (обобщающий урок)».
Выполнила:
учитель математики Панина Елена Юрьевна
МБОУ ЦО №8 Г. Тула
Технологическая карта урока геометрии в 11 классе по теме «Цилиндр. Площадь поверхности».
Панина Е.Ю. учитель математики высшая квалификационная категория
МБОУ ЦО №8 г. Тула
| Тема | Урок обобщение по теме ««Цилиндр. Площадь поверхности». |
| Цель урока |
|
| Задачи |
|
| Тип технологии обучения | личностно- ориентированная |
| Тип урока | обобщение и систематизация знаний( комбинированный) |
| Формы и методы обучения | индивидуальная, фронтальная работа; коллективное обсуждение, анализ; работа с тестами.
|
| Виды учебной деятельности |
|
| Ключевые компетенции |
|
| Основные понятия |
|
| Оборудование | Презентация « Решение задач по теме Цилиндр» PowerPoint по теме урока; проектор; компьютер |
| Планируемые образовательные результаты: | личностные
|
| Метапредметные
| |
| предметные знать
уметь
|
Организационная структура урока
| Структурные элементы урока | Дидактические элементы урока | Деятельность преподавателя | Деятельность учащихся |
| 1. Организационный момент | Монолог | Приветствует учащихся, проверяет готовность к уроку Здравствуйте, ребята. Садитесь. Тема нашего урока «Цилиндр, конус, шар» Сегодня весь урок мы посвятим обобщению знаний о площади поверхности цилиндра . Мы должны сегодня СЛАЙД 5
| Приветствуют учителя, готовятся к уроку |
| 2. Проверка домашнего задания |
| 1 ученик записал на доске решение задачи № 522: СДАЙД 6
Вопросы учащемуся:
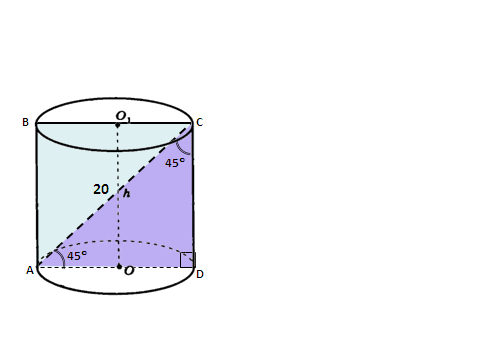
2 ученик записал на доске решение задачи № 523: СЛАЙД 7 Осевое сечение цилиндра – квадрат, диагональ которого равна 20 см. Найдите: а) высоту цилиндра; б) So цилиндра
Вопросы: СЛАЙД 8
|
Осевым сечением называется сечение, проходящее через ось цилиндра.
В результате такого сечения получится прямоугольник.
Я воспользовался соотношением сторон и углов в прямоугольном треугольнике.
Треугольник прямоугольный, равнобедренный.
Определение косинуса острого угла в прямоугольном треугольнике: косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе.
Надо знать радиус основания.
Радиус основания равен половине высоты.
|
| 3. Мотивация учебной деятельности | Диалог | Объявляет тему, цели и план занятия СЛАЙД 9 Мы завершаем изучение цилиндра. Цилиндр – первая фигура вращения, которую мы изучили. В дальнейшем мы изучим еще две фигуры, полученные аналогичным путем. Многие предметы в окружающем мире представляют собой цилиндр. Его изучение поможет решать практические задачи, возникающие в нашей жизни., Данная тема также включена в задания ЕГЭ.
| Записывают тему в тетрадь |
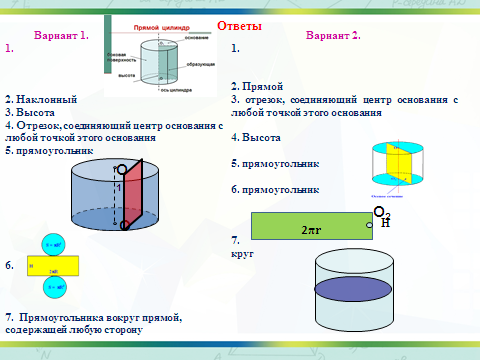
| 4. Актуализация знаний | Теоретическая разминка (фронтальный опрос)
Вопросы практической направленности
Математический диктант
| СЛАЙД 10-12
.
2) Почему цилиндр называют телом вращения?
3) Назовите виды цилиндров?
4) Назовите элементы цилиндра.
5) Что представляет собой развертка цилиндра?
6) Назовите основные виды сечений цилиндра. Какая фигура получается в каждом случае?
СЛАЙД 13
СЛАЙД 14
Учитель диктует вопросы учащимся СЛАЙД 16
|
Отвечают на вопросы Цилиндр – это геометрическое тело, состоящее из двух равных кругов, расположенных в параллельных плоскостях и множества отрезков, соединяющих соответственные точки этих кругов. Цилиндр можно получить вращением прямоугольника вокруг одной из его сторон.
Наклонные цилиндры, прямые цилиндры, цилиндрические поверхности. Радиус цилиндр; Высота цилиндра ; Основания цилиндра ; Ось цилиндра; Образующая цилиндра
Разверткой боковой поверхности цилиндра является прямоугольник со сторонами H и C, где H – высота цилиндра, а C – длина окружности основания.
Осевое сечение цилиндра Сечение плоскостью, параллельной оси цилиндра.
S=2πr(r+h)/
водонапорная башня/
достают чистые листочки, подписывают их и приступают к выполнению математического диктанта
Учащиеся на листках отвечают на вопросы.
Учащиеся сверяют ответы и оценивают свою работу СЛАЙД 15
|
| 5.Закрепление полученных знаний при решении задач |
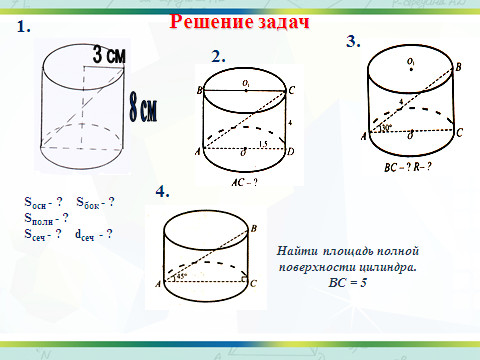
Решение задач по готовым чертежам
Решение задач прикладного характера
Решение задач исследовательского характера
| СЛАЙД 17-18
Предлагает решить задачи СЛАЙД19
Вопросы:
СЛАЙД 20
Вопросы:
r1, r2- радиусы оснований
|
Учащиеся решают задачи
Необходимо знать площадь полной поверхности цилиндра?
Площадь боковой поверхности и двух оснований.
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.
Площадь основания равна πr²
Учащиеся записывают решение в тетрадь:
r = 0,75 м S полн. =2πr ( r + h ) = 2 . 3,14 . 0,75 . (0,75 + 3) = 17,6625 м2, Надо площадь полной поверхности цилиндра умножить на количество краски на один квадратный метр .
17,6625 . 0,2 = 3,5325 кг. Ответ: 3,5325 кг.
Учащиеся записывают решение в тетрадь:
h1 = 2 h2 r2 = 2 r1
Sполн 1 = 2π r1 (r1 + h1) = 2 π r1 (r1 + 2h2) Sполн 2 = 2 π r2 (r2 + h2) = 2 2 π r1 (2r1 + h2)
Значит,Sполн 1 Ответ: на вторую деталь никеля потребуется больше.
|
| 6.Отработка навыков при решении задач по данной теме | Дистанционная обучающая система для подготовки к экзаменам «РЕШУ ЕГЭ» http://решуегэ.рф (http://reshuege.ru) | СЛАЙД 21-27 Учитель рассказывает алгоритм работы на сайте «Решу ЕГЭ»
Учитель записывает результат каждого учащегося и выставляет оценки. | Учащиеся выполняют последовательно: СЛАЙД 21-29
|
| 7.Рефлексия учебной деятельности. Итог урока | Диалог | СЛАЙД 32 Подведем итог работы на уроке.
| Отвечают на вопросы учителя Ученики отвечают на поставленный вопрос. На уроке мы изучали цилиндр. |
| 6. Домашнее задание | Монолог | Домашнее задание на карточке СЛАЙД 33 | Записывают домашнее задание |
.
.

 Получите свидетельство
Получите свидетельство Вход
Вход




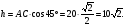
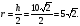
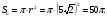











 Конспект урока по теме "Цилиндр. Площадь поверхности цилиндра" (465.35 KB)
Конспект урока по теме "Цилиндр. Площадь поверхности цилиндра" (465.35 KB)
 0
0 719
719 60
60 Нравится
0
Нравится
0


