Технологическая карта урока
Ф.И.О. учителя: Терентьева Елена Аркадьевна
Класс: 10
Дата:
Предмет: Геометрия
УМК: А.С. Атанасян «Геометрия 10-11»
Тема урока: «Полная и боковая поверхность призмы»
Тип урока: урок формирования новых знаний
Дидактическая цель урока: добиться осознания и осмысления того, что изучаемый на уроках геометрии материал по теме «Призма» может пригодиться при решении задач из жизни.
Задачи урока:
-
Обобщить и систематизировать имеющиеся у обучающихся сведения о призме.
-
Ввести понятие полной и боковой поверхности призмы.
-
Способствовать формированию умений применять теоретические знания к решению задач с практическим содержанием.
-
Формирование умений у обучающихся вести исследовательскую работу.
-
Способствовать формированию умений проводить оценку и самооценку знаний и умений.
-
Развивать логическое мышление, интерес к предмету, умение работать самостоятельно, в паре.
Методы обучения: словесные (метод самостоятельной работы с дидактическим материалом), наглядные (частично – поисковый), репродуктивный, исследовательский, управления познавательной деятельностью под руководством учителя, проблемного изложения.
Формы организации обучения: индивидуальная, фронтальная, парная, групповая.
Средства обучения: тетрадь, модели призм и других многогранников карточки с вопросами теста, карточки- памятки «Призма и ее элементы», карточки с заданиями.
Основные термины и понятия: призма, элементы призмы, площадь полной и боковой поверхности.
Планируемые образовательные результаты:
Предметные:
Знать элементы и виды призм. Формулы площадей полной и боковой поверхности призм.
Уметь применить знания о призме при решении практических задач.
Личностные: умение слушать и вступать в диалог, умение работать в паре, выработка ответственности и аккуратности.
Метапредметные: актуализировать полученные знания для решения практических задач.
Характеристика этапов урока
| Структура урока | Деятельность учителя | Деятельность учащихся | Формируемые УУД | ||||||||||||||||||||||||
| Мотивация (включение обучающихся в учебную деятельность) 1мин | Приветствует учащихся, создаёт доброжелательную рабочую атмосферу в классе, проверяет готовность рабочего места учителя и ученика. Здравствуйте, ребята. Урок я хотела бы начать со слов «Рано или поздно всякая правильная математическая идея находит применение в том или ином деле». А.Н.Крылов На уроке можно выдвигать гипотезы, ошибаться, сомневаться. Дайте себе установку: «понять, запомнить и уметь видеть решение» | Приветствуют учителя, концентрируют внимание, проверяют готовность своего рабочего места
| Личностные: -самоопределение; -смыслообразование Познавательные: -целеполагание Комутативные: - планирование учебного сотрудничества с учителем и одноклассниками | ||||||||||||||||||||||||
| Актуализация знаний (погружение в проблемную ситуацию) 5 мин Постановка проблемы 2 мин
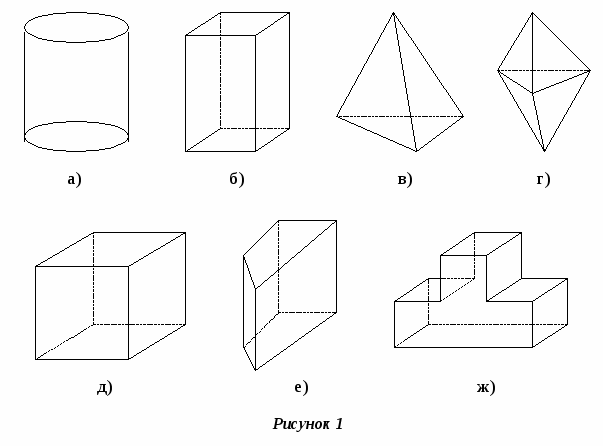
| Фронтальная работа На доске представлены многогранники. Прямоугольный Правильный параллелепипед тетраэдр Ребята вы можете пользоваться подсказками на раздаточном материале (Приложение 1) Вопросы к классу: – Назовите их. – Прямоугольный параллелепипед является частным случаем какого многогранника? - Дайте определение призмы - Назовите элементы призмы? - Какие виды призм бывают? -Что значит прямая призма? -Какая призма называется правильной? Ребята, а теперь давайте решим задачу. Рассчитайте сколько необходимо купить обоев, чтобы обклеить комнату в которой вы проживаете. -Что для этого нам необходимо знать? - Вы умеете это делать? - А если не возможности измерить высоту, например, в высотном доме. |
Отвечают на вопросы учителя.
-Прямоугольный параллелепипед и тетраэдр - Прямоугольный параллелепипед- это четырехугольная призма - призма – многогранник, состоящий из двух плоских многоугольников, лежащих в параллельных плоскостях и всех отрезков, соединяющих соответствующие точки этих многоугольников. Многоугольники называются основаниями призмы, а отрезки- боковыми ребрами. - Боковые ребра, вершины, основания, боковые грани - Призмы бывают прямыми и наклонными. -Прямая призма – это призма, в которой боковые ребра перпендикулярны плоскостям основания. Правильная призма- прямая призма, в основании которой лежит правильный многоугольник (квадрат, равносторонний треугольник и т.д.)
Ребята отвечают
Необходимо знать площади стен, т.е боковой поверхности. - Да, если измерить стороны основания и высоту призмы. Ребята формулируют затруднения. -Тогда нам необходимо знать какие- то определенные формулы. | Познавательные: - анализ, синтез, сравнение, обобщение, классификация; - осознанное и произвольное построение речевого высказывания; Регулятивные: - фиксирование индивидуального затруднения в проблемной ситуации; Коммуникативные: - выражение своих мыслей с достаточной полнотой и точностью; - аргументация своего мнения и позиции в коммуникации. Познавательные: - анализ, синтез, обобщение, сравнение; - постановка и формулирование; Коммуникативные: - выражение своих мыслей с достаточной полнотой и точностью; - аргументация своего мнения и позиции в коммуникации; - учет разных мнений , координирование разных позиций. | ||||||||||||||||||||||||
| Постановка темы урока 1 мин | Следовательно, какова тема нашего урока Записываем тему в тетрадь. Что нам сегодня надо узнать, чему научиться?
| Боковая и полная поверхность призмы. Узнать формулы вычисления боковой и полной поверхности призмы. Научиться решать задачи с применением данных формул. | Личностные: - самоопределение; -смыслообразование. Познавательные: -самостоятельное выделение и формулирование познавательной цели; | ||||||||||||||||||||||||
| Поиск решения (открытие нового знания) 12мин |
Ребята как вы думаете, что будет представлять собой полная поверхность призмы.
Давайте запишем в тетрадь формулу вычисления полной поверхности.
-Что необходимо знать, чтобы найти Sосн?
-Что представляет собой боковая поверхность?
Нахождение поверхности призмы является практически необходимым во многих сферах жизни человека. Но зачастую вычисление боковой поверхности призмы бывает затруднительным и трудоемким. Поэтому придумали формулу, упрощающую вычисления.
Выведем формулу вычисления боковой поверхности призмы. Для рассмотрения возьмем прямую треугольную призму и сделаем ее развертку.
-Что представляет собой развертка?
-Как вычислить площадь прямоугольника?
-В нашем случае, чем являются стороны прямоугольника?
- Сформулируем конечную формулу вычисления боковой поверхности призмы и запишем ее в тетрадь.
| - Сумма площадей всех граней призмы. Записывают формулу Sпол= Sбок+ +2Sосн, где S осн- площадь основания, Sбок- площадь боковой поверхности
-Формулы площадей треугольников, четырехугольников. - Площадь параллелограммов, лежащих в боковой поверхности.
- Прямоугольник (боковая поверхность) и два треугольника (основания) - Одну сторону умножить на другую -Одна сторона – это высота призмы, а вторая сторона прямоугольника складывается из сторон основания, т.е является периметром основания. Ребята вслух формулируют формулу: Боковая поверхность прямой призмы равна произведению периметра основания призмы на ее высоту S= Росн H, где Росн- периметр основания ( сумма длин всех сторон), H – высота призмы (длина бокового ребра). | Личностные: -смыслообразование; Познавательные: - поиск необходимой информации; - осознанное и произвольное построение речевого высказывания; Коммуникативные: - выражение своих мыслей с достаточной полнотой и точностью Регулятивные: - познавательная инициатива. | ||||||||||||||||||||||||
| Применение нового знания 8 мин | Работа в группах. Представим себе, что мы работаем в экономическом отделе предприятия по изготовлению упаковок для молока. Необходимо просчитать, какая упаковка будет экономически выгодна для производства: упаковка, имеющая форму правильного тетраэдра или упаковка, имеющая форму прямоугольного параллелепипеда. (Приложение 2) -Ребята проверим ваши вычисления и сделаем выводы. Таблица 1. Определение площади поверхности упаковки, имеющей форму прямоугольного параллелепипеда (вместимость – 0,2 литра)
Таблица 2. Определение площади поверхности упаковки, имеющей форму правильного тетраэдра (вместимость – 0,2 литра).
| Каждая группа получает карточку с таблицами, упаковки для сока. (Приложение 2) Выполняют задание на корточках: измеряют линейкой элементы прямоугольного параллелепипеда и тетраэдра, записывают в таблицу и вычисляют площади полной поверхности многогранника. Ребята озвучивают свои решения и делают вывод Экономия составит: на 1 упаковке – 46 см2; Вывод: экономически более выгодна будет упаковка, имеющая форму прямоугольного параллелепипеда. Поэтому в магазинах упаковку в виде правильного тетраэдра можно встретить очень редко. | Личностные: -осознание ответственности за общее дело; Познавательные: - выполнение действий по алгоритму; -осознанное и произвольное построение речевого высказывания; Коммуникативные: - формулирование и аргументация своего мнения и позиции в коммуникации; -достижение договоренности и согласование общего решения. | ||||||||||||||||||||||||
| Самостоятельная работа с самопроверкой | Выполним теперь самостоятельную работу (Приложение 3) А теперь обменялись работами со своим соседом и проверяем работу. Ответы вывешиваются на доску.(работа в парах) | Ребята выполняют тест на листочках. Ребята проверяют работы, выставляют оценки и сдают листочки учителю. | Познавательные: -выполнение действий по алгоритму; Регулятивные: - контроль; -коррекция; -оценка; Коммуникативные: - выражение своих мыслей с достаточной полнотой и точностью; - использование критериев для обоснования своего суждения. | ||||||||||||||||||||||||
| Домашнее задание1 мин | Дома придумать задачу практического содержания на тему «Площадь поверхности призмы.» | | | ||||||||||||||||||||||||
| Рефлексия 1мин | Предлагает ответить на вопросы: Какие знания приобрели на уроке? Чему научились? Какие умения продемонстрировали? | Рефлексируют: На этом уроке я приобрел следующие знания: Я научился: Я продемонстрировал умения: | Личностные: -адекватное понимание причин успеха/неуспеха в учебной деятельности; Познавательные: -рефлексия способов и условий действия; -контроль и оценка процесса и результатов деятельности; Коммуникативные: - выражение своих мыслей с достаточной полнотой и точностью -формулирование и аргументация своего мнения, учет разных мнений |
|
| ||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
| Прямая призма: Правильная призма: | ||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
| Одним из частных случаев призмы является ПАРАЛЛЕЛЕПИПЕД И КУБ | ||||||||||||||||||||||||||||||
| Полная поверхность призмы: полная поверхность призмы равна сумме площадей боковой поверхности и двум площадям основания S= Sбок+ 2 Sосн | ||||||||||||||||||||||||||||||
| Площадь боковая поверхности призмы: | ||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
Тест. 1 вариант.
1). Призма – это выпуклый многогранник, который состоит из:
а) многоугольника и нескольких параллелограммов
б) двух равных многоугольников и нескольких параллелограммов
в) двух равных многоугольников, лежащих в параллельных плоскостях,
и п параллелограммов
2). В основании призмы лежит:
а) любой выпуклый многоугольник
б) только правильный многоугольник
в) любой многоугольник или окружность
3). Призма является прямой, если:
а) боковые ребра перпендикулярны основаниям
б) основания – правильные многоугольники
в) некоторые боковые грани – квадраты
4). Призма является правильной, если:
а) в основании лежит правильный многоугольник
б) боковые грани перпендикулярны основаниям
в) она прямая и в основании лежит правильный многоугольник
5). Высотой прямой призмы можно считать:
а) ребро основания
б) боковое ребро
в) любой отрезок, перпендикулярный основанию
6). Площадь боковой поверхности призмы – это:
а) сумма площадей всех боковых граней
б) сумма площадей двух оснований
в) сумма площадей всех её граней
7). Площадь полной поверхности призмы – это:
а) сумма площадей всех боковых граней
б) сумма площадей двух оснований
в) сумма площадей всех её граней
8). Площадь боковой поверхности прямой призмы можно найти по формуле:
а) Sбок=Sосн·h
б) Sбок=а·h, где а – сторона основания
в) Sбок=Росн·h
9). Площадь полной поверхности прямой призмы можно найти по формуле:
а) Sполн=Sосн+ Sбок
б) Sполн=2Sосн+ Sбок
в) Sполн=2Росн+ Sбок
Тест. 2 вариант.
1). Призма – это выпуклый многогранник, который состоит из:
а) двух равных многоугольников, лежащих в параллельных плоскостях,
и п параллелограммов
б) двух равных многоугольников и нескольких параллелограммов
в) многоугольника и нескольких параллелограммов
2). В основании призмы лежит:
а) только правильный многоугольник
б) любой многоугольник или окружность
в) любой выпуклый многоугольник
3). Призма является прямой, если:
а) некоторые боковые грани – квадраты
б) боковые ребра перпендикулярны основаниям
в) основания – правильные многоугольники
4). Призма является правильной, если:
а) в основании лежит правильный многоугольник
б) она прямая и в основании лежит правильный многоугольник
в) боковые грани перпендикулярны основаниям
5). Высотой прямой призмы можно считать:
а) боковое ребро
б) любой отрезок, перпендикулярный основанию
в) ребро основания
6). Площадь боковой поверхности призмы – это:
а) сумма площадей всех её граней
б) сумма площадей двух оснований
в) сумма площадей всех боковых граней
7). Площадь полной поверхности призмы – это:
а) сумма площадей всех боковых граней
б) сумма площадей всех её граней
в) сумма площадей двух оснований
8). Площадь боковой поверхности прямой призмы можно найти по формуле:
а) Sбок=Росн·h
б) Sбок=Sосн·h
в) Sбок=а·h, где а – сторона основания
9). Площадь полной поверхности прямой призмы можно найти по формуле:
а) Sполн=Sосн+ Sбок
б) Sполн=2Росн+ Sбок
в) Sполн=2Sосн+ Sбок

 Получите свидетельство
Получите свидетельство Вход
Вход













 Наклонная призма:
Наклонная призма:










 Конспект урока по геометрии в 10 классе по теме "Полная и боковая поверхности призмы" (267.56 KB)
Конспект урока по геометрии в 10 классе по теме "Полная и боковая поверхности призмы" (267.56 KB)
 0
0 68
68 3
3 Нравится
0
Нравится
0



