8 класс
Геометрия
Автор учебника Атанасян Л.С.
Тема урока: Решение задач на нахождение площадей многоугольников.
Цель урока
Обобщить знания о площадях многоугольников.
Рассмотреть различные способы нахождения площадей многоугольников на клетчатой бумаге.
Воспитывать ответственное отношение к учебному труду, настойчивость для достижения конечного результата, умение работать самостоятельно, в группе, осуществлять самоконтроль.
Задачи урока
Повторить все известные формулы площадей многоугольников.
Решить задачи на нахождение площадей, используя формулы.
Научиться решать задачи нового типа.
Ход урока.
Актуализация знаний:
Опрос (доказательство теоремы о площади трапеции)
Повторение известных формул для нахождения площадей фигур
(одновременная работа учащихся на доске и в карточках/ технологических картах на местах, карточки заполняются формулами, против каждой фигуры записываются все возможные для нахождения площади изображённой фигуры)
| фигура | формула | фигура | формула |
| прямоугольник
|
|
|
|
| ромб со стороной а, диагоналями |
где p – полупериметр, |
гипотенузой c |
где p – полупериметр,
|
|
|
|
|
где p – полупериметр, для правильного: |
Решение задач на клетчатой бумаге на нахождение площади данной фигуры (самостоятельно, на карточках/технологических картах с последующей взаимопроверкой и демонстрацией решения на демонстрационной доске)
|
1 ___________________ |
2___________________ | 3______________________ |
Решение задач в тетради, по данным текстам задач. Фронтально, с записью решения на доске.
Площадь параллелограмма равна 48 см2, а его периметр 40 см. Найти стороны параллелограмма, если высота, проведённая к одной из них, в 3 раза меньше этой стороны.
В ромбе ABCD диагонали равны 5 и 12 см. На диагонали АС взята точка М так, что АМ : МС=4:1. Найдите площадь треугольника AMD.
Решение задач на нахождение площадей фигур по готовым чертежам
(работа ведётся в парах, полуустно, с записью только необходимых формул и вычислений, на карточках/технологических картах)
| 1. АВСД – параллелограмм Найти ВК. | 4. Найдите площадь треугольника АВС. | 7. Найти S |
| 2. Найти S | 5. Найти площадь трапеции АВСД | 8.Найти S |
| 3 Найдите площадь треугольника АВС. | 6 Найдите площадь треугольника АВС. | 9. AC=12, S=48, найти BD |
Повторить свойства площадей.
Решение задач на применение свойств площадей, с выбором необходимой формулы, последовательности действий.
Найти площади данных треугольников, изображённых на рисунках.
(задача 1 – решение комментируется,
задача 2 – самостоятельно, с проверкой ответа)
Задача 1 Задача 2
Итог урока
Площади каких фигур находились в течение урока? (многоугольников)
Какие подходы использовались при решении задач? (1 – с использованием формул, 2 – с использованием свойств площадей)
Какие дополнительные сведения повторили/пригодились на уроке?
Домашнее задание.
В равнобедренном треугольнике АВС высота BH равна 12 см, а его основание АС в 3 раза больше высоты BH. Найдите площадь треугольника АВС.
В параллелограмме ABCD стороны равны 14 и 8 см, высота, проведенная к большей стороне, равна 4. Найдите площадь параллелограмма и вторую высоту.
Площадь трапеции равна 320см2 , а высота трапеции равна 8 см. Найдите основания трапеции, если длина одного из оснований составляет 60% длины другого.
Приложение
Технологическая карта
Записать формулу, по которой можно найти площадь изображённой фигуры
| фигура | формула | фигура | формула |
| прямоугольник
|
|
|
|
| ромб со стороной а, диагоналями |
|
гипотенузой c |
|
|
|
|
|
|
Найти площадь фигуры, изображённой на клетчатой бумаге
Решить задачу в тетради, выполнив к ней рисунок1 ___________________
2___________________
3______________________
Площадь параллелограмма равна 48 см2, а его периметр 40 см. Найти стороны параллелограмма, если высота, проведённая к одной из них, в 3 раза меньше этой стороны.
В ромбе ABCD диагонали равны 5 и 12 см. На диагонали АС взята точка М так, что АМ : МС=4:1. Найдите площадь треугольника AMD.
Решить задачи на готовых чертежах, с записью необходимых формул
1.
АВСД – параллелограмм
Найти ВК.
4.
Найдите площадь треугольника АВС.
7. Найти S
2.
Найти S
5.
Найти площадь трапеции АВСД
8.Найти S
3
Найдите площадь треугольника АВС.
6
Найдите площадь треугольника АВС.
9.
AC=12, S=48, найти BD
Найти площади данных треугольников, изображённых на рисунках.
(задача 1 – решение комментируется,
задача 2 – самостоятельно, с проверкой ответа)
| Задача 1 | Задача 2 |
|
|
|
| Решение | Решение |
| Ответ | Ответ |
Домашнее задание.
В равнобедренном треугольнике АВС высота BH равна 12 см, а его основание АС в 3 раза больше высоты BH. Найдите площадь треугольника АВС.
В параллелограмме ABCD стороны равны 14 и 8 см, высота, проведенная к большей стороне, равна 4. Найдите площадь параллелограмма и вторую высоту.
Площадь трапеции равна 320см2 , а высота трапеции равна 8 см. Найдите основания трапеции, если длина одного из оснований составляет 60% длины другого.

 Получите свидетельство
Получите свидетельство Вход
Вход




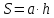
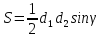
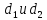
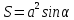
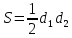
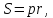
 прямоугольный, с катетами a, b
прямоугольный, с катетами a, b 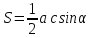
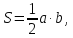 где a,b - катеты
где a,b - катеты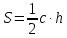

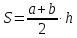
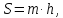 где m – средняя линия
где m – средняя линия









 Конспект урока по геометрии на тему "Решение задач по теме Площади многоугольников" (8 класс, геометрия) (1.02 MB)
Конспект урока по геометрии на тему "Решение задач по теме Площади многоугольников" (8 класс, геометрия) (1.02 MB)
 0
0 469
469 59
59 Нравится
0
Нравится
0


