Тема урока: «Длина окружности. Площади фигур»
Цели урока:
Образовательные: Повторить все изученные формулы площадей и формулу длины окружности; познакомить учащихся с новым измерительным прибором; закрепить навыки решения практических задач.
Развивающие: Развивать внимательность, логическое мышление, навыки самостоятельной и коллективной работы, расширять кругозор учащихся.
Воспитательные: Воспитывать познавательный интерес к урокам геометрии, чувство
ответственности, культуру общения.
Тип урока: Урок практикум.
Оборудование: Компьютер, проектор, экран, доска, мел. У каждого ученика модель круга, модель цилиндра или конуса, центроискатель, линейка, калькулятор.
Ход урока:
Организационный момент (сообщение темы и целей урока)
Актуализация знаний учащихся.
Повторение формул площадей, изученных в курсе планиметрии; формулы длины окружности и длины дуги окружности.
На экране появляются формулы, учащиеся называют площадь какой фигуры можно вычислить по данной формуле.
|
|
|
|
|
|
| S=a2 | S=ab |
|
| C=2πR |
|
| S=πR2-πr2 |
|
|
|
Выполнение практических заданий
Задание 1.
Учитель: Дети, у каждого из вас на столе модель круга. Как найти его площадь?
Учащиеся: Нужно знать радиус круга. Чтобы измерить его нужно знать, где находится центр круга.
Учитель: Как найти центр круга?
Учащиеся: Перегнуть пополам круг два раза.
Учащиеся находят центр круга, измеряют радиус и вычисляют площадь.
Задание 2.
Учитель: У вас на столах цилиндры и конусы. Как вычислить площадь основания данной фигуры? Где будет центр окружности основания?
Учащиеся затрудняются ответить.
Учитель: Можно использовать специальный прибор, который называют «центроискателем» (у каждого на столе лежит этот прибор). Он представляет собой угольник, длина одной из сторон которого вдвое больше ширины другой стороны ( АВ=2КС). Вдоль кромки ВС расположена равномерная шкала, масштаб которой вдвое больше масштаба шкалы, расположенной вдоль кромки МК (В и М точки начала шкал). Чтобы отыскать центр заданной окружности, центроискатель прикладывают так, чтобы вершины А и В лежали на окружности. Тогда центр окружности совпадает с делением шкалы МК, имеющим то же числовое значение, что и точка, в которой окружность пересекает шкалу ВС.
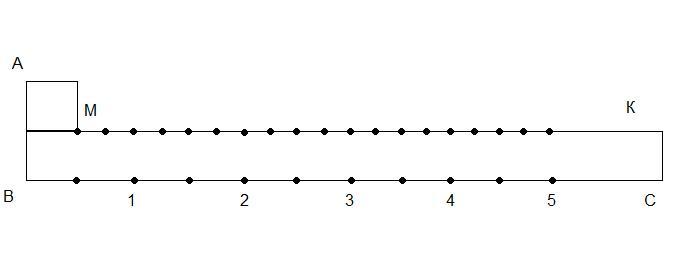
Учащиеся ищут центр основания цилиндра и конуса с помощью центроискателя, измеряют радиус, вычисляют площадь основания фигур.
Задание 3. Предположим, что земной шар по экватору плотно обтянут веревкой. Её длину увеличивают на 1 м. Будем считать, что образовавшийся зазор равномерно распределили по всему экватору. Сможет ли в этот зазор прошмыгнуть мышь?
Решение:


С1=2πR1 С2=2πR2
C2-C1=1 м
2π(R2-R1)=1
R2-R1=1:(2π)=0,1592…м =16 см
Ответ: может
Вопрос: Изменится ли зазор, если не земной шар, а футбольный мяч сначала был обтянут плотно веревкой, а затем длину её увеличили на 1 м?
Заслушать ответы, можно провести эксперимент с мячом, веревкой и линейкой.
Ответ: не изменится.
Решение задач на готовых чертежах
Работа в группах с последующей проверкой. Каждая группа получает задание соответствующего уровня сложности. Один представитель группы записывает решение на доске и поясняет его.








C
№1. Площадь квадрата АВСD равна 16. Найти длину окружности
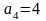

B
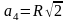
D
A
№2. Найти площадь заштрихованной на рисунке фигуры, если ВС=4, угол ВАС=30ᵒ.
АС –диаметр круга.
B
AC=8, R=4, AB=
A
C
Sкруга =16π
S =
№3. Вычислите площадь заштрихованной на рисунке фигуры, если АО=4, угол АОВ=135ᵒ.
F
E
D
С
В
А
№4. Около шестиугольника ABCDEF описана окружность, а в треугольник АСЕ вписана окружность радиуса 2. Найти площади треугольника, шестиугольника и кольца, заключенного между окружностями.r3=2, R3=4, a3=R√3=4√3
R6 =4= a6, r6=
S6=
Sкольца =πR2-πr2=16π-4π=12π
Дополнительные сведения.
Внимание! Черный ящик!
То, что лежит в черном ящике, изобрел талантливый юноша; говорят, он же придумал гончарный круг и первую в мире пилу. Под пеплом Помпеи археологи обнаружили много таких предметов, изготовленных из бронзы. В нашей стране этот предмет был обнаружен при раскопках в Нижнем Новгороде. В Древней Греции умение пользоваться этим предметом считалось верхом совершенства. А умение решать задачи с его помощью- признаком большого ума. Этот предмет незаменим в архитектуре и строительстве. За многие сотни лет конструкция его не изменилась. В настоящее время им умеет пользоваться любой школьник.
Вопрос: Что лежит в черном ящике?
Ответ: Циркуль.
Подведение итогов, выставление оценок, задание на дом.

 Получите свидетельство
Получите свидетельство Вход
Вход



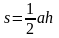
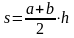
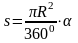
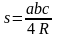
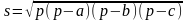
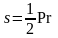
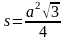
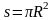
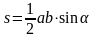
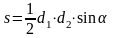
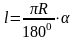









 Конспект урока по геометрии на тему "Длина окружности. Площади фигур" (115.83 KB)
Конспект урока по геометрии на тему "Длина окружности. Площади фигур" (115.83 KB)
 0
0 344
344 31
31 Нравится
0
Нравится
0


