Тема урока: Теорема Пифагора. Работа с текстовым редактором.
Эпиграф: «Мысль – превыше всего между людьми». Заповедь Пифагора.
Цель: создать «карту памяти» (интеллект-карту) по теме «Теорема Пифагора» средствами текстового редактора.
Ход урока
Организационный момент.
Здравствуйте дети. Сегодня у нас необычный урок. Ведут урок два учителя … На уроке «встречаются» два предмета: геометрия и информатика. Рассматриваются две различные темы, по геометрии: «Теорема Пифагора», по информатике: «Работа с текстовым редактором». Но цель урока одна: создать «карту памяти» по теме «Теорема Пифагора» с помощью текстового редактора.
Актуализация опорных знаний.
Повторение теории теорема Пифагора.
На протяжении нескольких уроков мы с вами изучаем тему: «Теорема Пифагора». Давайте восстановим логическую цепочку определений, теорем, пояснений по данной теме.
Фронтальная работа с классом.
Определение косинуса острого угла в прямоугольном треугольнике
Теорема о косинусе угла (формулировка).
Следствия из теоремы Пифагора.
Теорема, обратная теореме Пифагора (формулировка).
Египетский треугольник.
Пифагоровы тройки.
Главная теорема темы – это терема Пифагора. Она носит имя известного древнегреческого мыслителя математика, религиозного и политического деятеля Пифагора.
На предыдущих уроках мы много говорили с вами о жизни Пифагора, о его школе, о его учении. Мы знаем с вами, что Пифагор оставил после себя много заповедей. Одна из них является эпиграфом нашего урока «Мысль – превыше всего между людьми».
Учитель: В чем смысл теоремы Пифагора?
Ученик: Она устанавливает связь между длинами сторон в прямоугольном треугольнике.
Учитель: Для чего нужна теорема Пифагора?
Ученик: Доказывать теоремы, решать задачи.
Устная работа.
– Решаем устно задачи (для быстрого счета применяем Пифагоровы тройки). (Задачи представлены на интерактивной доске, дети собирают пазл со своей фотографией, где они образуют прямоугольный египетский треугольник).
- Какой треугольник вы построили собой?
- Что это за треугольник?
- Зачем его используют?
- Что вы сделали, построив его?
3) Рассмотрение исторических задач.
- Как использовалась теорема Пифагора в других странах и нашими предками. (Доклад учащегося с презентацией решения исторических задач.)
III. Практическая работа по созданию карты.
- Приступаем к составлению «карты памяти», для этого используем инструменты текстового редактора.
Напомним рекомендации для создания «карты памяти»:
Используйте только ключевые слова или, где это возможно, изображения.
Начинайте создание карты с центра страницы.
Используйте цвет красный, синий, черный (обладают высокой степенью восприятия).
Создайте подтемы (5-7).
Используйте стрелки, значки, чтобы показать связь между различными подтемами.
Пишите печатными буквами. Это делает карту более читаемой и запоминающейся.
- Работаем за компьютерами парами, при этот соблюдает чувство толерантности друг к другу.
Толерантность – это не просто способность «терпеть рядом другого» - это умение «сотрудничать с другими»; договариваться, находить точки соприкосновения, идти на компромиссы. Умение «мирно убедить другого» в своей правоте, отстоять свое мнение.
IV. Защита «карты памяти».
- Зачем нужна карта?
(Навести порядок в голове по данной теме, получить целостную картину, помогает выучить материал, помочь однокласснику).
V. Задание на дом.
Создать эмблему урока, ответив на вопрос: «Какие фигуры можно построить на сторонах прямоугольного треугольника, чтобы выполнялась теорема Пифагора?»
Косинус угла. (новолат. cosinus)
β


A
B



ΔACB – прямоугольный (ﮮС=90о)
ﮮА+ﮮB=90о
α
C
| Cos α= | Cos β= |
| AC=AB*cosα | BC=AB*cosβ |
| AB= | AB= |
Т.(о косинусе угла)




 cosA=
cosA=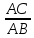 =
=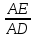 =
=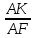
F
D
B
K
E
C
A
Теоремма Пифагора
с² = а² + в²
а² = с² - в²
в² = с² - а²
Т. (обратная Т. Пифагора)
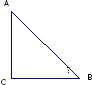
Если а² + в² = с², то ﮮС = 90º
Пифагоровы тройки
3, 4, 5
6, 8, 10
5, 12, 13
8, 15, 17

 Получите свидетельство
Получите свидетельство Вход
Вход



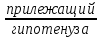
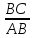 =
=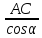
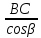









 Конспект интегрированного урока по теме "Теорема Пифагора" (66.87 KB)
Конспект интегрированного урока по теме "Теорема Пифагора" (66.87 KB)
 0
0 549
549 19
19 Нравится
0
Нравится
0


