Материал на украинском языке.
Мета уроку:
навчальна: ознайомити учнів з поняттям «правильний многогранник», навчити розрізняти правильні многогранники, визначати кількість граней, вершин та ребер,
розвивальна: познайомити учнів з галузями, де зустрічаються правильні многогранники, їх цінність для науки, розвивати пізнавальний інтерес,
виховна: виховувати інтерес до вивчення математики, естетичну культуру.
Хід уроку.
І. Організаційний момент.
ІІ. Актуалізація знань учнів.
Математичний диктант «Вірю – не вірю»
(викладач диктує твердження, а учні на листочках ставлять «+» , якщо твердження правильне, або «-», якщо ні, кожна правильна відповідь – 0,5 бала, по закінченню, учні взаємоперевіряють роботу, якщо учень бажає оцінка заноситься до журналу)
1. (+) Всі бічні грані піраміди - трикутники
2. (+) Висота прямої призми дорівнює її висоті
3. (+) Трикутна піраміда має 4 грані
4. (+) Апофема правильної піраміди довша за її висоту
5. (+) П’ятикутна призма має 15 ребер
6. (+) Бічні грані правильної піраміди – рівнобедрені трикутники
7. (-) Бічні грані зрізаної піраміди – паралелограми
8. (-) Чотирикутна призма має 4 грані
9. (+) Основи призми рівні і паралельні
10. (-) Будь-яка грань призми – паралелограм
11. (+) Бічне ребро піраміди може дорівнювати висоті
12. (+) Трикутна призма має 6 вершин.

ІІІ. Мотивація навчальної діяльності учнів.
Викладач: У житті і практичній діяльності ми часто зустрічаємось із многогранниками, а тому нам потрібно добре знати їх характеристики, властивості і вміти застосовувати їх для розв’язування різноманітних задач.
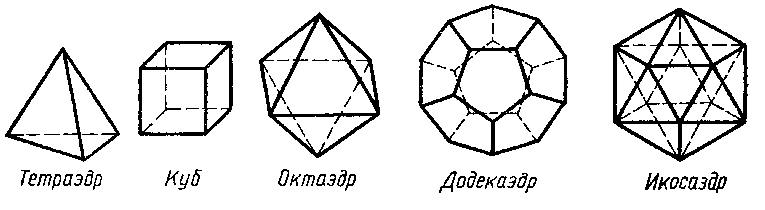
Сьогодні ми завершуємо вивчення теми «Многогранники», в якій вивчили призму і піраміду, нам залишилось познайомитись з п’ятьма многогранниками - особливо красивими.
Це правильні многогранники. Крім цього ми вивчимо нові латинські слова, поєднаємо математику з хімією, фізикою, біологією та іншими науками.
Епіграф:
«Немає жодної галузі математики, якою б абстрактною вона не була, що коли-небудь не виявиться застосованою для явищ дійсного світу» М. І. Лобачевский.
ІІІ. Вивчення нового матеріалу.
Визначення правильних многогранників, які даються в різних підручниках, рекомендованих для загальноосвітніх шкіл, є багато. Розглянемо декілька з них
«Опуклий багатогранник називається правильним, якщо всієї його грані – правильні багатокутники й у кожній його вершині сходиться однакова кількість ребер». (Л.С. Атанасян «Геометрія, 10-11 класи»)
“Багатогранник називається правильним, якщо всі його грані - рівні правильні багатокутники, а всі його вершини однаково віддалені від деякої точки - центра правильного багатокутника” (Г. П. Бевз, В. Г. Бевз, Н. Г. Владимирова. Геометрія 7-11 класи )
“Якщо всі грані опуклого багатогранника - конгруентні правильні багатокутники й число ребер, що виходять із кожної вершини, однаково, то багатогранник називається правильним” (В. М. Клопський, З. А. Скопець, М. И. Ягодовський. Геометрія. Навчальний посібник для 9-10 класів середньої школи).
Їх ще називають платоновими тілами.
Спробуйте визначити найголовніше з прочитаних означень та записати в «робочий зошит»
Запишемо основні властивості правильних многогранників:
- всій його грані рівні правильні багатокутники.
- всі плоскі кути рівні,
- всі двогранні кути, що містять дві грані із загальним ребром, рівні,
- всі ребра рівні,
- всі багатогранні кути рівні,
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход













 Конспект уроку з геометрії "Правильні многогранники" (73.4 КB)
Конспект уроку з геометрії "Правильні многогранники" (73.4 КB)
 0
0 1730
1730 198
198 Нравится
0
Нравится
0


