Цель урока:
- расширить представления об определении положения точки на плоскости, сформировать представления о координатной плоскости; ввести понятия «координатная плоскость», «прямоугольная система координат», «начало координат», «оси координат», «ось абсцисс», «ось ординат», «координаты точки», «абсцисса точки», «ордината точки», «координатная четверть».
Выполнить учебные задания на определение координат точек по их расположению на координатной плоскости и по записи: точек, расположенных на координатных осях, точек, расположенных в I (II, III, IV) координатной четверти
- развивать у учащихся интерес к математике;
- формировать в процессе обучения математике таких качеств личности, как самостоятельность, настойчивость, любознательность.
Ход урока.
1. Организационный момент.
2. Актуализация знаний.
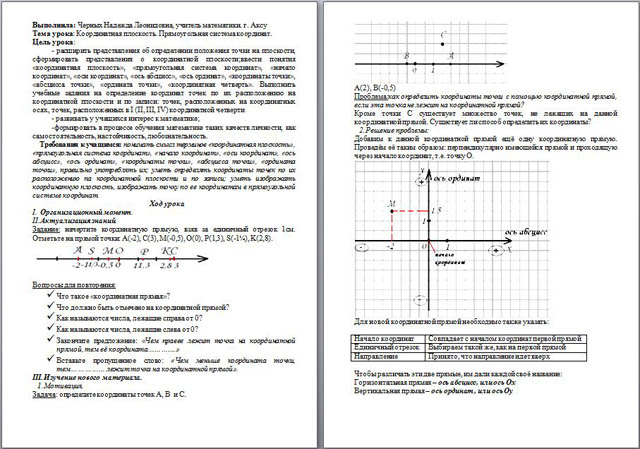
Задание: начертите координатную прямую, взяв за единичный отрезок 1см. Отметьте на прямой точки: A(-2), C(3), M(-0,5), O(0), P(1,3), S(-1¼), K(2,8).
Вопросы для повторения:
- Что такое «координатная прямая»?
- Что должно быть отмечено на координатной прямой?
- Как называются числа, лежащие справа от 0?
- Как называются числа, лежащие слева от 0?
- Закончите предложение: «Чем правее лежит точка на координатной прямой, тем её координата….»
- Вставьте пропущенное слово: «Чем меньше координата точки, тем…… лежит точка на координатной прямой».
3. Изучение нового материала.
1. Мотивация.
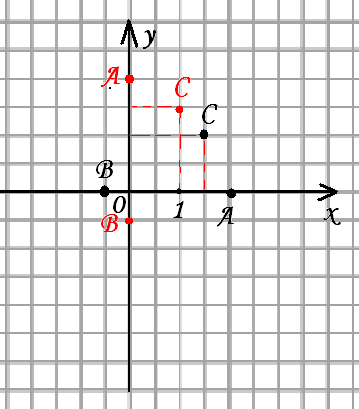
Задача: определите координаты точек A, B и С.
A(2), B(-0,5)
Проблема:как определить координаты точки с помощью координатной прямой, если эта точка не лежит на координатной прямой?
Кроме точки C существует множество точек, не лежащих на данной координатной прямой. Существует ли способ определить их координаты?
2. Решение проблемы:
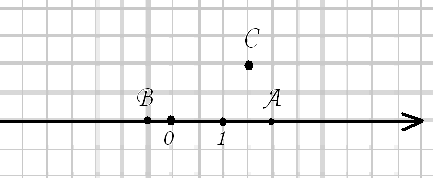
Добавим к данной координатной прямой ещё одну координатную прямую. Проведём её таким образом: перпендикулярно имеющейся прямой и проходящую через начало координат, т.е. точку О.
Чтобы различать эти две прямые, им дали каждой своё название:
Горизонтальная прямая – ось абсцисс, или ось Ох
Вертикальная прямая – ось ординат, или ось Оу
Возникает вопрос: мы знаем, что на оси х координаты правее 0 – положительные, а левее 0 – отрицательные. Как в таком случае располагаются координаты на оси у?
Выше 0 – положительные.
Ниже 0 – отрицательные.
Где вы видели ещё вертикальное расположение координат с таким же направлением? (термометр)
Итак, заданы оси х и у, т.е. определены их направление, единичные отрезки и начало координат. Это значит, что задана система координат.
Система координат – это две перпендикулярные координатные прямые х и у, которые пересекаются в начале отсчета – точке О.
Точку О называют началом координат.
Но мы ещё не решили проблему: как же определять координаты точки в системе координат?
Чтобы определить координаты точки М в системе координат, нужно из точки М провести перпендикуляры на оси абсцисс и ординат. Затем определим координаты на каждой из координатных прямых:
На оси х получилось -2 – это абсцисса точки М (или координата по оси х)
На оси у получилось 1,5 – это ордината точки М (или координата по оси у)
Тогда координата точки М будет записана таким образом: М(-2; 1,5)
На первом месте записывается абсцисса точки, на втором – ордината.
Переставлять координаты точки местами нельзя!
Оси координат делят плоскость на четыре прямых угла. Их называют координатными углами или координатными четвертями. Стр.
А) Определите координаты точек A, B и С в системе координат.
Сделаем вывод:
Точки с ординатой 0 лежат на оси х
Верно и другое:
Точки с абсциссой 0 лежат на оси у.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



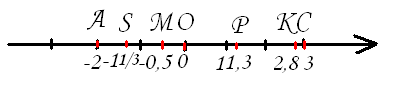









 Конспект урока по математике "Прямоугольная система координат" (61.65 КB)
Конспект урока по математике "Прямоугольная система координат" (61.65 КB)
 0
0 2289
2289 261
261 Нравится
0
Нравится
0


