Цели: вычисление неопределенного интеграла способом подстановки, используя свойства и формулы интегрирования
Тип урока: урок усвоения нового материала
Наглядные пособия: таблица формул интегрирования
Ход урока:
Организационный момент.
Этап подготовки учащихся к активному сознательному усвоению знаний.
Этап усвоения новых знаний:
- теоретический материал
Приложение 1
Практический материал
Приложение 2
4. Этап закрепления:
- Самостоятельное вычисление примеров через воспроизведение действий по образцу
Приложение 3
4. Этап информации о домашнем задании:
Вычислить неопределенные интегралы способом подстановки:
Приложение 1
Метод подстановки в неопределенный интеграл
Если заданный интеграл с помощью алгебраических преобразований трудно или невозможно свести к одному или нескольким табличным интегралам, то для его отыскания применяют особые способы, одним из которых является способ подстановки (замены переменной).
Заметим, что все способы интегрирования имеют целью свести данный интеграл к табличному с помощью тех или иных искусственных приемов.
Способ подстановки заключается в следующем: заменяют новой переменной такую часть подынтегральной функции, при дифференцировании которой получается оставшаяся часть подынтегрального выражения (не считая постоянного множителя, на который всегда можно умножить и разделить подынтегральное выражение).
Приложение 2
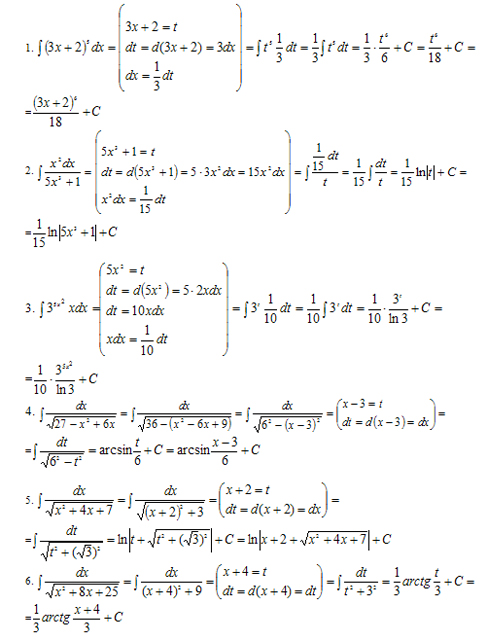
Правило интегрирования способом подстановки состоит в следующем:
Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно).
Определяют, какую часть подынтегральной функции заменить новой переменной, и записывают эту замену.
Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной.
Производят замену под интегралом.
Находят полученный интеграл.
В результате производят обратную замену, то есть переходят к старой переменной. Результат полезно проверить дифференцированием.
Полную информацию смотрите в файле.

 Получите свидетельство
Получите свидетельство Вход
Вход



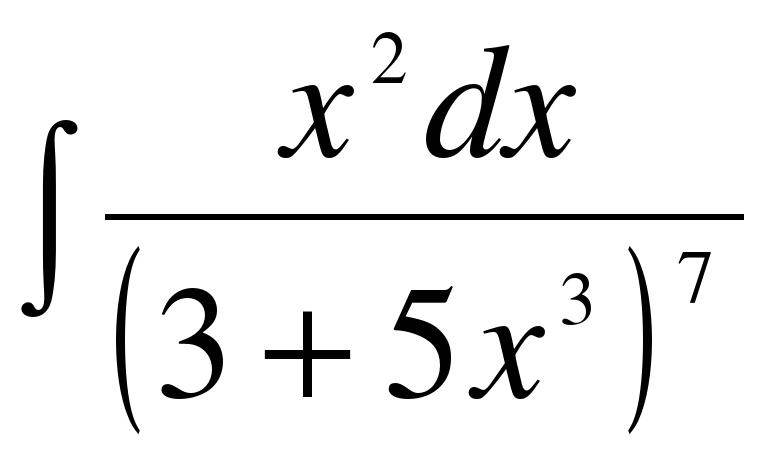
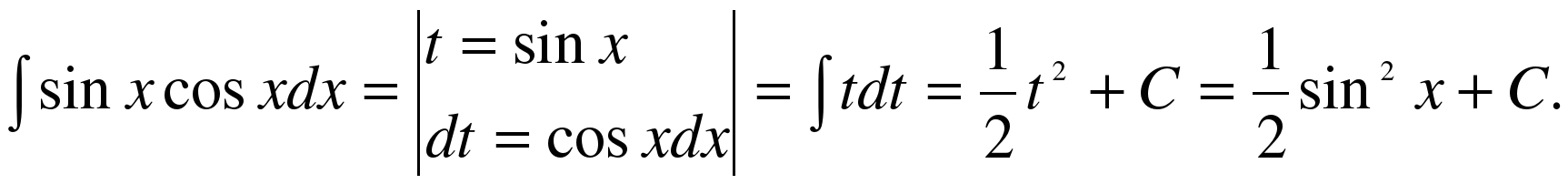
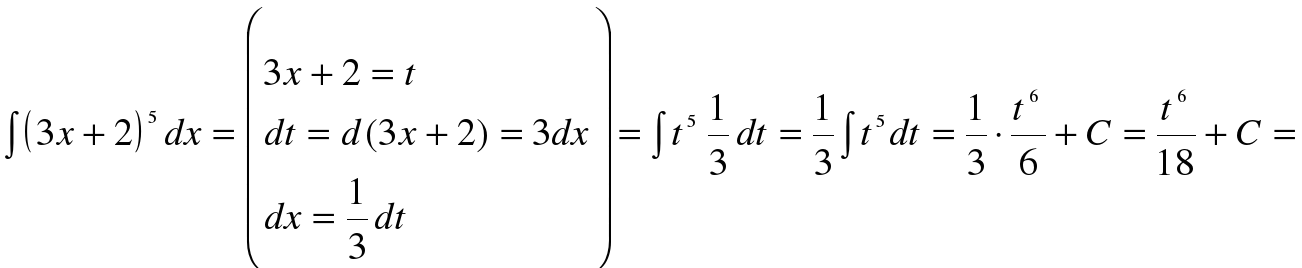
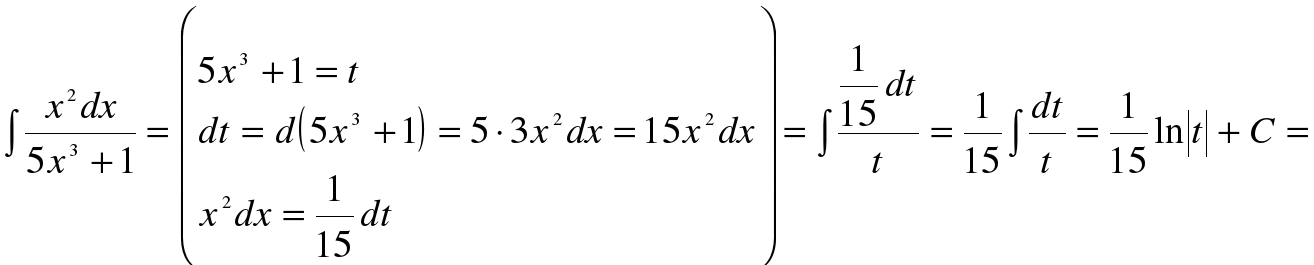
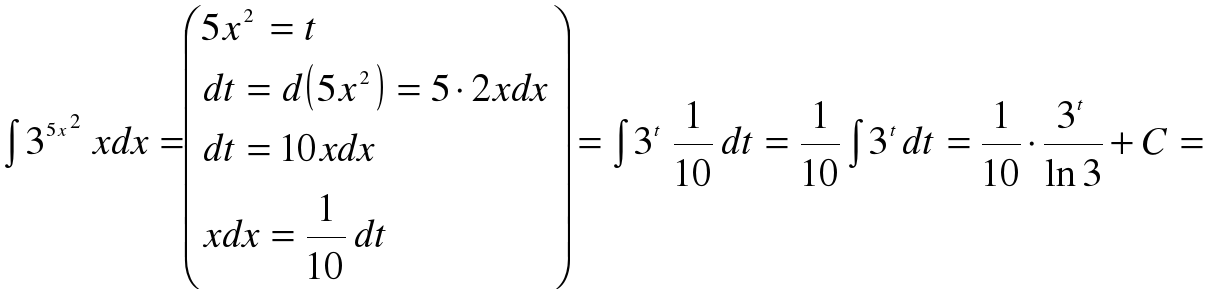
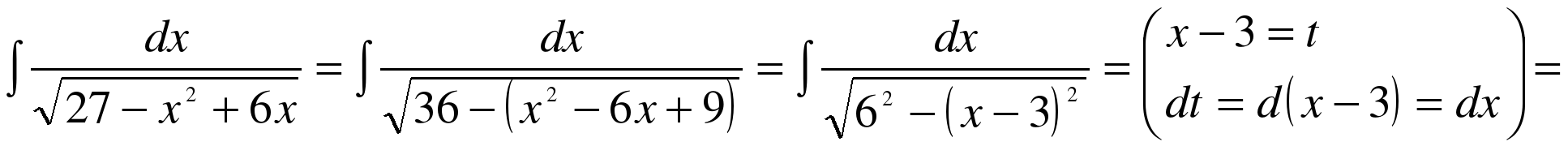
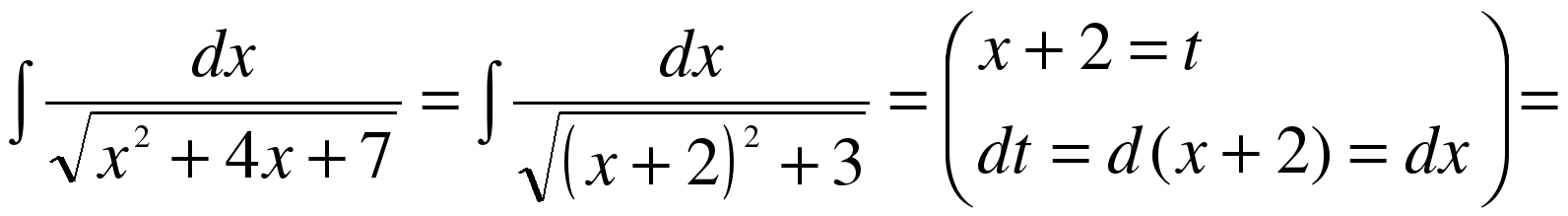









 Конспект урока по математике на тему "Метод подстановки в неопределенном интеграле" (0.12 MB)
Конспект урока по математике на тему "Метод подстановки в неопределенном интеграле" (0.12 MB)
 0
0 1241
1241 227
227 Нравится
0
Нравится
0


