Цели урока:
Образовательные:
– систематизировать и контролировать уровень усвоения знаний, умений и навыков по нахождению суммы n-первых членов арифметической прогрессии;
– формировать умения и навыки по нахождению суммы n-первых членов арифметической прогрессии в решении упражнений.
Воспитательные:
– содействование формированию мировоззренческих понятий;
– развитие познавательного интереса учащихся к предмету;
– развитие памяти и внимания.
Развивающие:
– развитие учащихся самостоятельности в учебной деятельности;
– формирование учащихся геометрической интерпретации изученной формулы;
– развитие логического мышления.
Оборудование к уроку: презентация к уроку, интерактивная доска.
План урока.
1. Организационный момент.
2. Опрос учащихся: а) Устные упражнения; б) У доски по карточкам.
3. Изучение нового материала.
4. Закрепление изученного материала.
5. Самостоятельная работа.
6. Подведение итогов урока. Оценки на уроке. Домашнее задание.
Ход урока.
1. Оргмомент. Тема урока, цели урока.
2. Опрос учащихся.
Устно.
Является ли последовательность четных чисел арифметической прогрессией?
Найдите 10 член арифметической прогрессии, если а1=1, а разность равна 4.
Дана конечная ариф. прогрессия а1;а2;а3;а4;а5;а6, разность=d
Является ли арифметической прогрессией последовательность
а) а2;а4;а6
б) а1-2; а2-2; а3-2; а4-2; а5-2; а6-2?
У доски. Карточка №1.
Найдите а1 арифметической прогрессии, если а36=90, а разность d=2.
В уловом секторе стадиона в 1 ряду 7 мест, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в 26 ряду? (из ЕГЭ)
Карточка №2.
Какое число не является членом арифметической прогрессии: 4; 7; 10; 13; …?
Ответ:
1) 31; 2) 32; 3) 34; 4) 37.

Задания по образцу:
Задана арифметическая прогрессия (аn), где а1 =7; d=2; n=20. Найти Sn.
Задана арифметическая прогрессия (аn), где а1 =7; d=2; n=10. Найти Sn.
Задана арифметическая прогрессия (аn), где а1 =5; d=2; n=12. Найти Sn
Задана арифметическая прогрессия (аn), где а1 =6; а20=52. Найти Sn.4. Закрепление нового материала.
Учитель: математику учить надо за то, что она ум в порядок приводит. Математика миру подарила формулы, которые позволяют делать различные расчеты. Перед нами стоит задача научиться применять формулы суммы n-первых членов арифметической прогрессии.
Задача.
В угловом секторе стадиона в 1 ряду 7 мест, а в каждом следующем на 2 больше, чем в предыдущем секторе. Сколько мест на стадионе, если рядов в нем 34?
Задачи из учебника:
№ 369(в) ; № 370(в) ; №372(а).
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



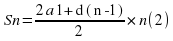
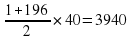 2 группа:
2 группа: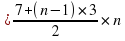 =(7n+3n2-3n)/2=(4n+3n2)/2=2n+1.5n2
=(7n+3n2-3n)/2=(4n+3n2)/2=2n+1.5n2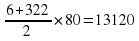
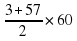 =30∙60=1800
=30∙60=1800








 Конспект урока по математике «Формула суммы n-первых членов арифметической прогрессии» (28.94 КB)
Конспект урока по математике «Формула суммы n-первых членов арифметической прогрессии» (28.94 КB)
 0
0 1707
1707 532
532 Нравится
0
Нравится
0


