Компьютерные программы для проведения интересных уроков математики в школе

Компьютерные программы по геометрии

Выполнила: Христофорова Анастасия Владимировна

Компьютерные программы по геометрии

• Wingeom

• Geogebra

• Poly

• Kig

• Математический конструктор 1С

Wingeom (Wgeomru)

• Лицензия:  Freeware 1985-2009
• (свободное пользование)
• Автор:  Richard Parris
• Язык интерфейса:  русский
• Сайт:  http://math.exeter.edu/rparris
• Описание:  Wingeom является геометрической программой и предназначена для создания точных, аккуратных, перемещающихся чертежей (2D-моделирование), трехмерных моделей (3D-моделирование), моделей неевклидовой геометрии (сферической и гиперболической), мозаик-паркетов.

Программа Wingeom обладает возможностями:

• 1)создавать точные, аккуратные модели плоских и пространственных фигур:    а) с использованием координат точек (вершин) фигуры;    б) заданием готовых фигур;    в) удалением элементов из готовой фигуры;    г) добавлением элементов к готовой фигуре;    д) создание сечений пространственных фигур.
• 2)трансформировать готовые изображения:    а) способ изменения изображения (дискретный, непрерывный);    б) вид изображения пространственных фигур (в центральной проекции, параллельной проекции, ортогональной проекции);    в) перемещение фигуры (удаление, приближение, наклон, вращение, смещение);    г) анимация;
• 3)редактировать построенные модели:    а) выделять (толщина, цвет, стрелки, невидимые линии);     б) удалять элементы (точки, линейные элементы, криволинейные элементы);
• 4)производить необходимые измерения:    а) длина отрезка;      б) величина угла в градусах;     в) площадь многоугольника;    г) периметр многоугольника;    д) отношение длин отрезков;    е) координаты точки;    ж) величина двугранного угла;

• з) величина (в стерадианах) многогранного угла;    и) длина дуги окружности;    к) длина окружности;    л) площадь круга, сечения многогранника;    м) радианная мера угла;    н) объем шара, конуса
• 5)применять геометрические преобразования:    а) параллельный перенос;    б) нормальный перенос;    в) поворот;    г) гомотетия;    д) зеркальная симметрия;    е) инверсия;
• 6)работать с текстом и обозначениями точек:    а) ввод и удаление текста и обозначений;    б) редактирование текста и обозначений (цвет, тип шрифта, размер шрифта);    в) привязка текста (к фигуре, к рамке);
• 7)сохранять историю создания модели; 8)показать построение модели в медленном режиме (презентация); 9)использовать макрос (макро-построения).

• Название программы:  Poly
• Платформа (ОС):  Windows
• Название компании:  Pedagoguery Software
• Лицензия:  условно бесплатная
• Сайт:  http:// www.peda.com/poly
• Язык интерфейса:  английский

Poly

•   Poly - программа для того, чтобы исследовать многогранные поверхности. Программа может показать многогранные поверхности тремя главными способами: • как трехмерное изображение, • как плоская, двумерная развертка, и • как топологическое вложение в плоскость.
• Трехмерные изображения могут в интерактивном режиме вращаться, сворачиваясь/разворачиваясь. Физические модели могут быть произведены, если распечатать плоские двумерные развертки, разрезать по периметру, свернуть по краям, и склеить лентой вместе соседние грани.
• Poly включает все особенности Poly и добавляет способность экспортировать многогранные модели, используя стандартные 3d форматы файлов (DXF, STL, 3DMF). С программой Pro Poly Вы можете также экспортировать вращающиеся многогранники как анимационные файлы GIF. Статические изображения могут экспортироваться как GIF или PCX файлы.

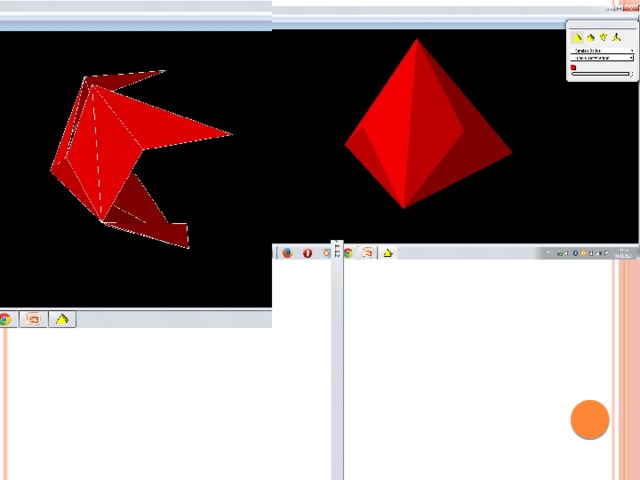
«Интерактивная геометрия (Kig)»

• Kig  - приложение для интерактивных геометрических построений, позволяющее ученикам и студентам изучать геометрические фигуры с помощью компьютера.
• Программа позволяет: а) исследовать и строить различные многогранники и их развертки; б) перемещать и вращать многогранные тела; в) распечатать развертки, которые можно вырезать и сложить для получения трехмерных моделей; г) создавать Платоновы тела (тетраэдр, гексаэдр, октаэдр, додекаэдр и икосаэдр), Архимедовы тела (усеченный тетраэдр, кубооктаэдр, усеченный куб, и многое другое), призмы и антипризмы (треугольные, пятиугольные, шестигранные и т.д.).  д) генерировать Джонсона тела и многое другое.

GeoGebra

• Категория:  геометрическое ПО
• Язык программирования:  Java
• Платформа (ОС):  Windows, Linux, MacOS
• Название компании:  Macrovision
• Лицензия:  GPL (General Public License) свободно распространяемая лицензия
• Авторы:  Markus Hohenwarter (Австрия, США),
• Сайт:  http://www.geogebra.org/
• Язык интерфейса:  русский

Систему можно использовать для построения линий:

• построение графиков функций y = f (x);
• построение конических сечений:
• коника произвольного вида — по пяти точкам.
• Окружность по центру и точке на ней, по центру и радиусу, по трем точкам;
• эллипс – по двум фокусам и точке на кривой;
• парабола – по фокусу и директрисе;
• гипербола – по двум фокусам и точке на кривой;

Кроме графических действий в системе могут быть выполнены вычисления:

• действия с матрицами: сложение, умножение; транспонирование, инвертирование; вычисление определителя;
• вычисления с комплексными числами;
• нахождение точек пересечения кривых;
• статистические функции:
• вычисление математического ожидания, дисперсии;
• вычисление коэффициента корреляции;
• Аппроксимация множества точек кривой заданного вида: полином; экспонента; логарифм; синусоида.

Geogebra имеет вид

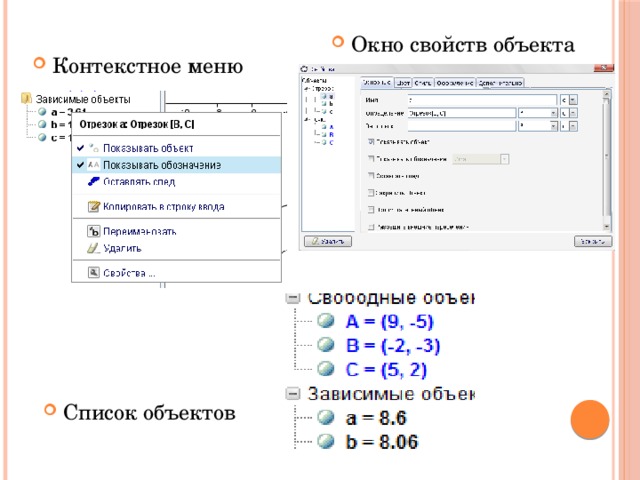
• Окно свойств объекта

• Контекстное меню

• Список объектов

• Задача 1. Треугольник АВС задан точками: А (9;–5), В (–7;–8), С (–5;–2). С помощью программы GeoGebra необходимо:

• 1) найти периметр треугольника;
• 2) найти уравнения сторон треугольника;
• 3) найти уравнение медианы АМ ;
• 4) найти уравнение высоты BH ;
• 5) найти уравнение прямой, проходящей через вершину A параллельно стороне ВC ;
• 6) найти радиус описанной окружности.

• построить вершины треугольника АВС
• А=(9, –5) В=(–2, –3) С=(5, 2)

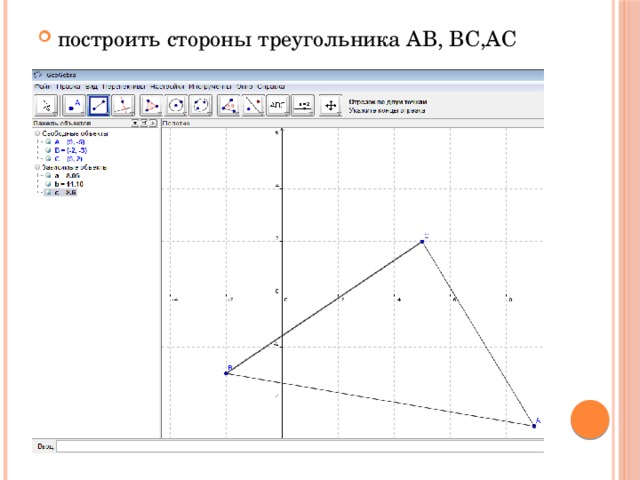
• построить стороны треугольника AB, BC,AC

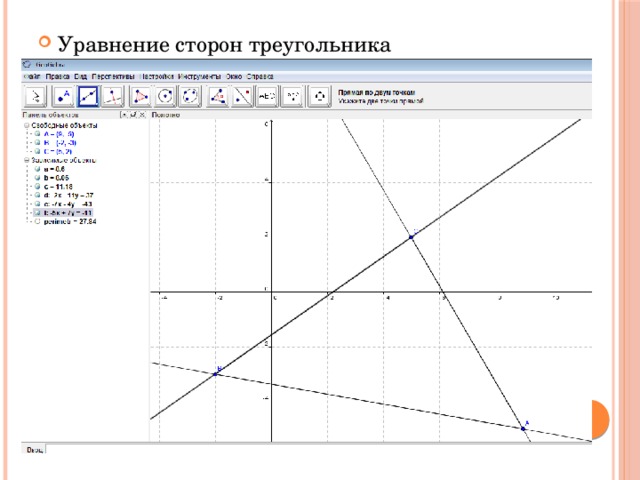
• Уравнение сторон треугольника

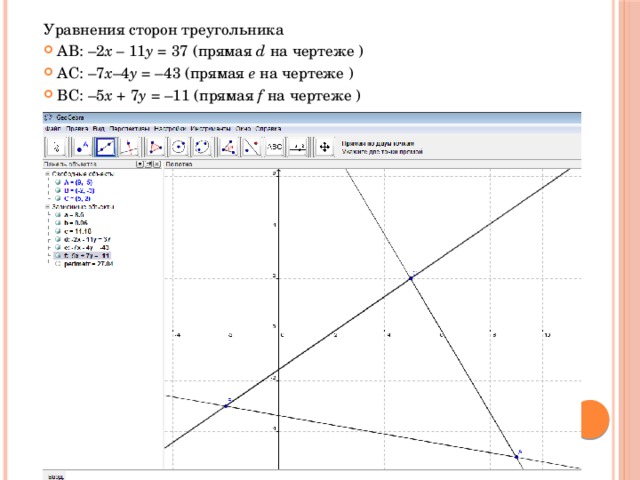
Уравнения сторон треугольника

• AB: –2 x –  11 y  = 37 (прямая d на чертеже )
• АС: –7 х –4 y  = –43 (прямая e на чертеже )
• BC: –5 x  + 7 y  = –11 (прямая f на чертеже )

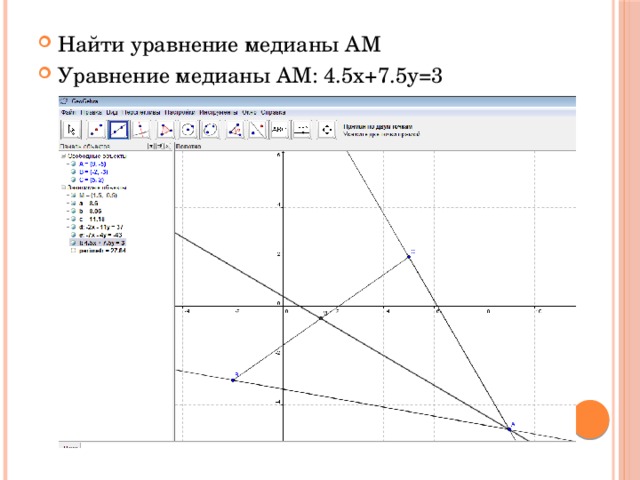
• Найти уравнение медианы АМ
• Уравнение медианы АМ: 4.5x+7.5y=3

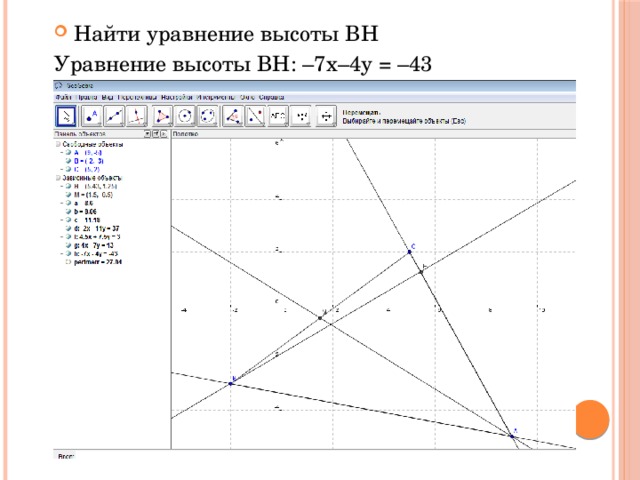
• Найти уравнение высоты BH 

Уравнение высоты BH: –7х–4y = –43

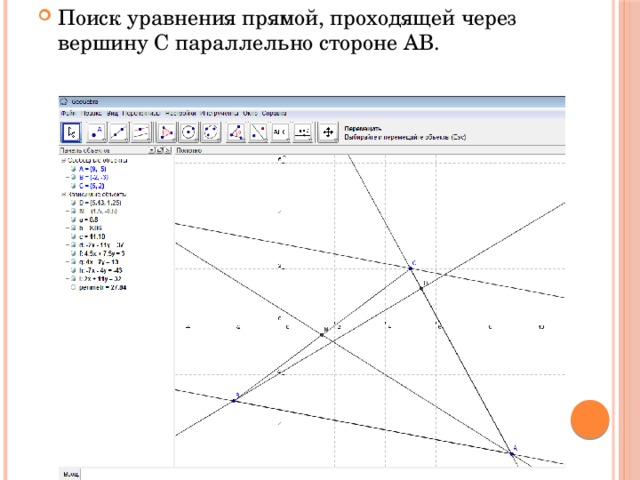
• Поиск уравнения прямой, проходящей через вершину С параллельно стороне АВ.

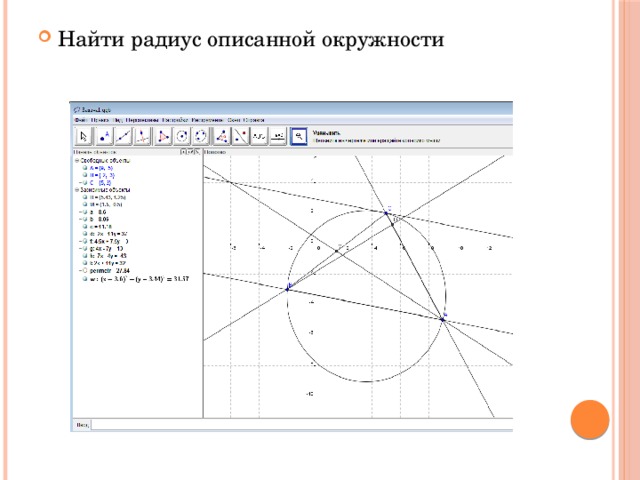
• Найти радиус описанной окружности

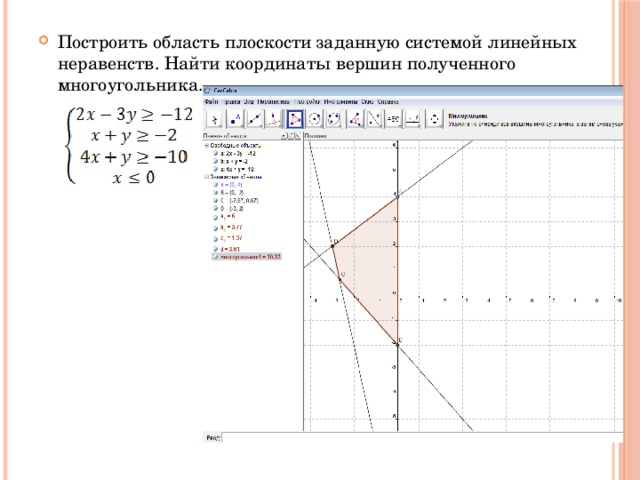
• Построить область плоскости заданную системой линейных неравенств. Найти координаты вершин полученного многоугольника.

«Математический конструктор 1С»

« Математический конструктор» – незаменимый помощник автора учебных материалов, в том числе учителя. В простейшем случае он позволяет легко создавать качественные рисунки для вставки в печатные тексты.

Возможности «Математического конструктора»:

• Динамические геометрические построения
• Измерения и вычисления
• Функции и графики
• Конические сечения и другие кривые
• Области и операции над ними
• Автоматическая проверка построений и тестов
• Текстовый редактор с вводом формул
• Построение анимаций
• Экспорт рисунков и апплетов
• Настройка панелей инструментов в моделях
• Интуитивно понятный интерфейс
• Пользовательские инструменты и скрипты
• Коллекция интерактивных обучающих моделей
• Создание аккуратных чертежей и графиков
• Самостоятельное исследование и эксперимент
• Быстрые построения при работе на уроке
• Организация проектной деятельности учащихся
• Создание обучающих и контрольных материалов

Спасибо за внимание!