Комбинация тел вращения с пирамидой и призмой.

Цели и задачи урока:

Образовательные:

Учащиеся должны знать:

• Какие условия нужны, чтобы одна геометрическая фигура была вписана в другую геометрическую фигуру стереометрии;

• Что такое высота и апофема;

• Теорему Пифагора для решения задач;

Учащиеся должны уметь:

• Вычислять нужную величину с помощью теоремы Пифагора;

• Сделать необходимый чертёж к решению задачи;

• Применять свойства геометрических фигур к условиям задачи;

Развивающие:

• развивать интерес к предмету;

• усвоить материал по теме урока;

• развивать у учащихся умение концентрироваться, слушать, а так же логическое мышление, речь, внимание, воображение.

Воспитательные:

воспитывать системность, самостоятельность, этику взаимоотношений.

Тип урока: комбинированный.

Ход урока

1. Организационный момент.

1. Актуализация знаний учащихся. Подготовка к активной учебно-познавательной деятельности на основном этапе урока.

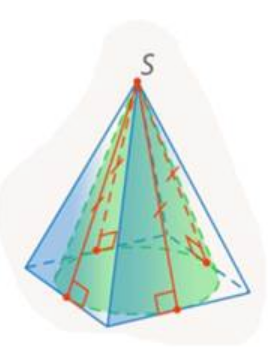Рис. 1

Вопросы к рис. 1 :

Ответ: Это значит, что стороны основания пирамиды должны быть касательными к окружности основания конуса.

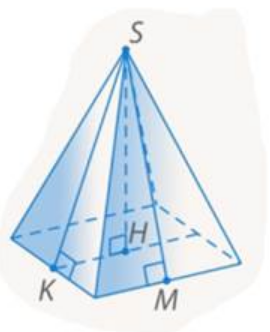Рис. 2

Ответ: Апофемами являются отрезки SK и SM, а высотой пирамиды является

отрезок SH.

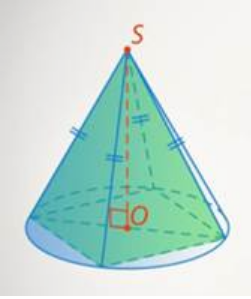Рис 3.

Вопрос к рис.3 : А как можно описать конус вокруг пирамиды?

Ответ: Нужно условие совпадение вершин и теперь основание пирамиды должно быть вписано в основание конуса – то есть все вершины основания пирамиды должны лежать на окружности основания конуса.

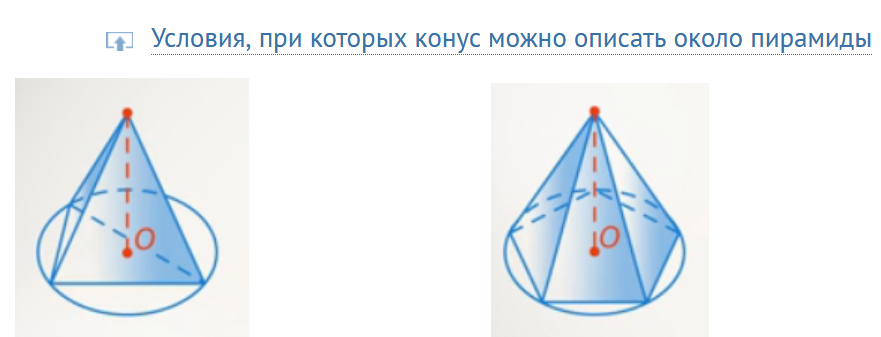
В случае треугольной и шестиугольной пирамиды эти условия так же выполняются.(Смотреть ответ на вопрос к рис.3)

1. Разбор домашнего задания.

Решение задачи из учебника № 630.

1. Новая тема урока: Комбинация цилиндра и призмы.

Цилиндр вписан в призму (или призма описана около цилиндра), если основания цилиндра вписаны в соответствующие основания призмы. Очевидно, что их высоты совпадут.

Смотрим рисунки:

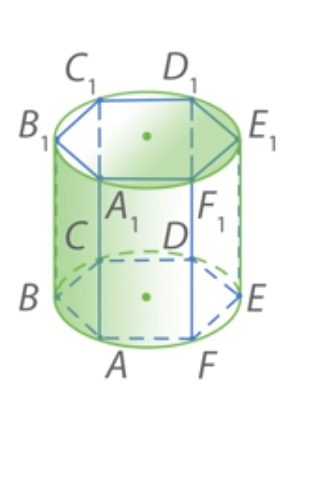
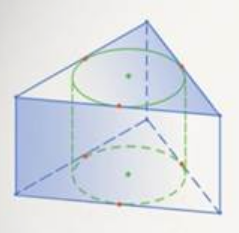
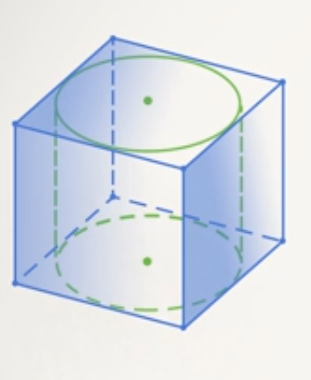
Вывод: цилиндр можно вписать в призму, если призма прямая, а в ее основание можно вписать окружность. И призму можно вписать в цилиндр с теми же условиями.

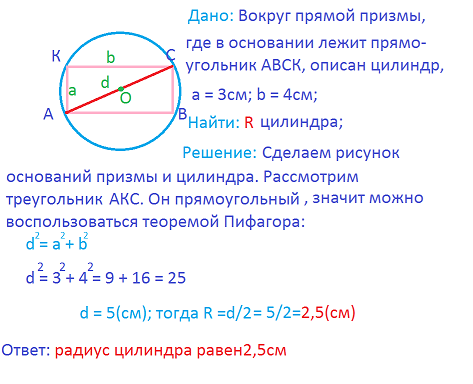
Решим задачу:

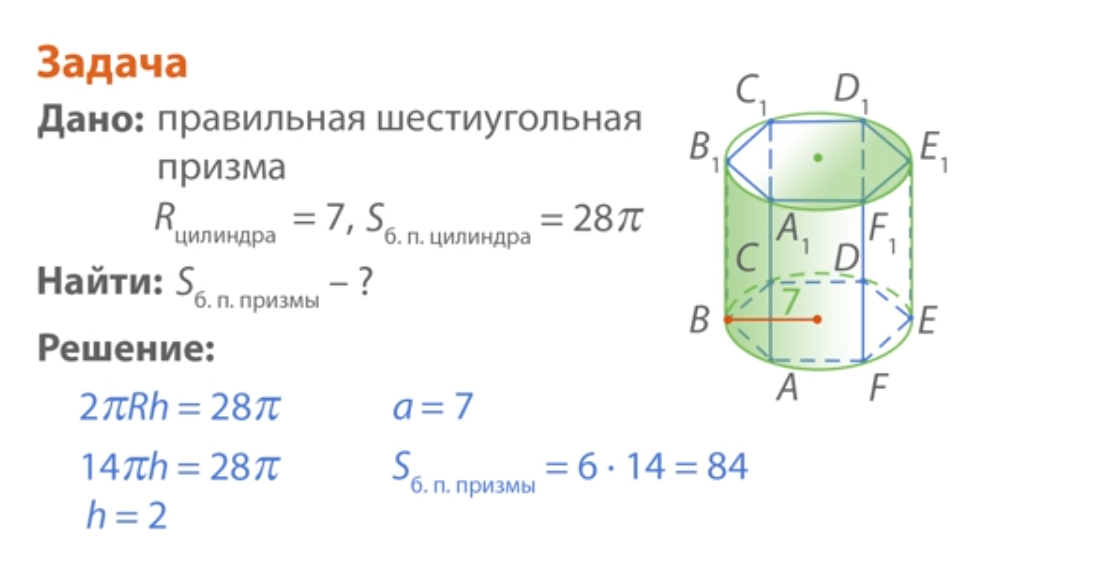Следующая задача:

1. Заключение:

Сегодня на уроке мы разобрали комбинации призмы и цилиндра, а также решили задачи по теме: цилиндр, описанный вокруг шестиугольной призмы и цилиндр, описанный вокруг прямой четырёхугольной призмы.

Домашнее задание : учебник стр. 146 задача № 634.

Выставление оценок.