
Количество движения. Импульс. Импульс силы материальной точки и тела. Закон сохранения импульса.

План:
- Количество движения-Импульс.
- Импульс силы материальной точки.
- Импульс силы тела.
- Закон сохранения импульса.

- Как мы рассмотрели прошлой лекции, второй закон Ньютона имеет следующей вид: F = m а.
- Как нам известно, ускорение это есть изменение скорости по времени. Поэтому дифференциальном виде ускорению можно написать через скорость следующем виде: а= d ϑ/ dt . Уравнение второго закона Ньютона можно придать другой вид:
F = m ( d ϑ/ dt ) (1).
- Учтя, что масса m в классической механике есть величина постоянная, ее можно внести под знак производной и записать (1) следующем образом:
F = d ( m ϑ)/ dt (2).

- Векторную величину р= m ϑ (3)
- называют импульсом материальной точки. Воспользовавшись определением импульса, уравнение второго закона Ньютона можно написать в виде: F = d р/ dt (4)
- а сам закон сформулировать: производная импульса материальной точки по времени равна результирующей всех сил, действующих на точку.

- Уравнение (4) справедливо в более широких приделах чем в (1). Как устанавливается теория относительности, масса тела является функцией скорости: с увеличением скорости масса растет. Правда, зависимость массы от скорости такова, что при скоростях значительно меньше скорости света, масса остается практически постоянной. Однако при больших скоростях масса начинает быстро расти, вследствие чего (1) становится неприменимым. В тоже время (4) остается справедливым и при этих условиях. Т.о., (4) сохраняет свое значение и в релятивисткой механике.

- Умножив (4) на dt , придем к соотношению: d р= F dt (5)
- интегрирование которого дает приращение импульса за промежуток времени, протекший от момента t 1 до момента t 2 :
(6)
- В частности, если F= const , формула (6) дает для приращения импульса за промежуток времени τ значение: p 2 – p 1 =F τ .

- Рассмотрим систему состоящих из N материальных точек. Тела, входящие в систему, могут взаимодействовать между собой, так и с телами, не принадлежащими данной системе. В соответствие с этим силы, действующие на тела системы, можно подразделить на внутренние и внешние. Внутренними мы будем называть силы, с которыми на данное тело воздействуют остальные тела системы, внешними – силы обусловленные воздействием тел, не принадлежащих системе.
- В случае, если внешние силы отсутствуют, система называется замкнутой.

- Импульсом системы р называется векторная сумма импульсов тел, образующих систему.
- Назовем центром инерции системы точку положение которой в пространстве задается радиусом вектором r c , определяемым следующем образом:
(7)
- где m i - масса i –го тела, r i - радиус вектор, опреде-ляющий положение этого тела в пространстве, m - масса системы.

- Декартовы координаты центра инерции равны проекциям r c на координатные оси:
х с = ∑ m i х i / m ; y c = ∑ m i y i / m ; z с = ∑ m i z i / m (8)
- Отметим, что центр инерции совпадает с центром тяжести системы.
- Скорость центра инерции получается путем дифференцирование r c по времени:
ϑ с = d r c /dt = ∑ m i (d r i /dt )/ m =∑ m i ϑ i / m (9).
- Учитывая, что m i ϑ i есть p i , а ∑ p i дает импульс системы p , можно написать
p=mϑ с (10).

- Пусть система состоит из трех тел (рис.1). Каждой из внутренних сил, например F 12 т.е. силе, с которой на тело 1 воздействует тело 2, соответствует сила F 21 , с которой тело 1 воздействует на тело 2, причем по третьему закону Ньютона F 12 = -F 21 . Символами F 1 , F 2 и F 3 обозначены результирующие всех сил, с которыми внешние тела воздействуют соответственно на 1-е, 2-е и 3-е тело системы. Напишем для каждого из трех тел уравнение (4)
d p 1 /dt = F 12 +F 13 + F 1 ,
d p 2 /dt = F 21 +F 23 + F 2 ,
d p 3 /dt = F 31 +F 32 + F 3 .
- Сложим все три уравнения вместе. Сума внутренних сил будет равна нулю, вследствие чего
d( p 1 + p 2 + p 3 )/dt= d p /dt = F 1 +F 2 + F 3 (11).
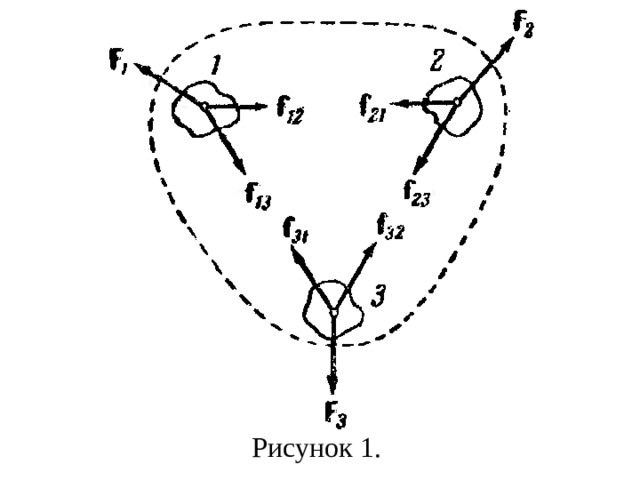
Рисунок 1.

- При отсутствие внешних сил получается, что d p /dt = 0 . Следовательно, для замкнутой системы p постоянен. Этот результат легко обобщить на систему, состоящую из произвольного числа тел N . Пользуясь сокращенной записью сумм, (4) для всех N тел можно представить следующем образом:
( i = 1,2,3…N) (12).
- Выражение (12) представляет собой систему N уравнений, отличающихся друг от друга значением индекса i . Суммирование каждом из этих уравнений производится по индексу k , причем в i –м уравнении индекс k пробегает все значения от 1 до N , кроме значения i=k .

- Складывая эти уравнения, с учетом того, что F ik =-F ki получим:
(13).
- Следовательно, производная по времени от вектора импульса системы равна векторной сумме всех внешних сил, приложенных к телам системы.
- Для замкнутой системы правая часть соотношения (13) равна нулю, вследствие чего p не зависит от времени. Это утверждения представляет собой содержание закона сохранения импульса, которой формулируется следующем образом: импульс замкнутой системы материальных точек остается постоянным. Отметим, что импульс остается постоянным и для системы, подверженной внешним воздействием, при условии, в сумме дают нуль.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Количество движения. Импульс (90.7 KB)
Количество движения. Импульс (90.7 KB)
 0
0 366
366 3
3 Нравится
0
Нравится
0





