Треугольник
B 3 № 27543.
На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
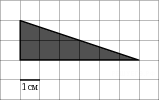
Решение.
Площадь прямоугольного треугольника равна половине произведения его катетов. Поэтому
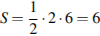 см2.
см2.
Ответ: 6.
|
| B 3 № 27544. На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
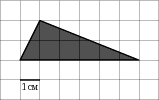
Решение. Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию. Поэтому 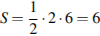 см2. см2. Ответ: 6. |
B 3 № 27545. На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
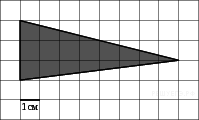
Решение.
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию. Поэтому
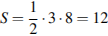 см2.
см2.
Ответ: 12.
B 3 № 27547. На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
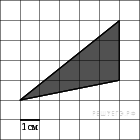
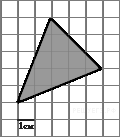
Решение.
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию или его продолжению. Выберем за основание вертикальную сторону, длиной 3 клетки. Тогда проведенная к ней из левой нижней вершины труегольника высота равна 5 клеткам (см. рис.). Поэтому
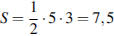 см2.
см2.
Ответ: 7,5.
B 3 № 27548. На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
Решение.
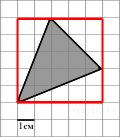 Площадь треугольника равна разности площади прямоугольника и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому
Площадь треугольника равна разности площади прямоугольника и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому
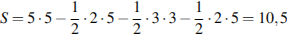 см2.
см2.
Ответ: 10,5.
B 3 № 27549. На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
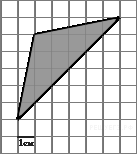
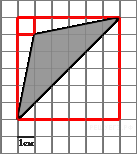 Площадь треугольника равна разности площади большого квадрата, маленького квадрата и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому
Площадь треугольника равна разности площади большого квадрата, маленького квадрата и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому
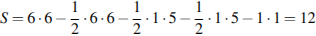 см2.
см2.
Ответ: 12.
|
| B 3 № 27617. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10. 
Решение. Площадь прямоугольного треугольника равна половине произведения его катетов. По теореме Пифагора a2 = 100 − 36 = 64, a = 8, где a — второй катет. Поэтому 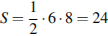 . . Ответ: 24. |
B 3 № 27623. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?
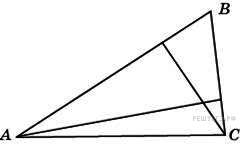
Решение.
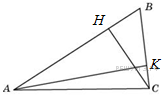
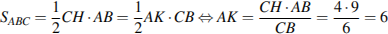 .
.
Ответ: 6.
Прямоугольник
B 3 № 27550. На клетчатой бумаге с клетками размером 1 см  1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.

Решение.
Площадь прямоугольника равна произведению длины на ширину. Поэтому
см2.
Ответ: 28.
|
| B 3 № 27551. Найдите площадь квадрата ABCD, считая стороны квадратных клеток равными 1. Решение. Площадь квадрата равна разности площади прямоугольника и четырех равных прямоугольных треугольников, гипотенузы которых являются сторонами исходного квадрата. Поэтому см2. Ответ: 10. |
B 3 № 27584. Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 4 и 9.
Решение.
Площадь прямоугольника равна произведению длины на ширину . Площадь квадрата равна квадрату его стороны. Поэтому сторона квадрата, площадь которого равна 36, равна 6.
Ответ: 6.
|
| B 3 № 27600. Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой.
Решение. Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, тогда вторая равна a+3. Периметр будет соответственно равен P = 2  a + 2 a + 2  (a + 3) = 18, (a + 3) = 18, тогда одна из сторон будет равна 3, а другая 6. Поэтому S = 3  6 = 18. 6 = 18. Ответ: 18. |
B 3 № 27601. Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны.
Решение.
Площадь прямоугольника равна произведению его длины на ширину. Пусть одна из сторон прямоугольника равна a, тогда вторая равна a + 3. Поэтому S = a  (a + 3) = 18, получаем a2 + 3a − 18 = 0, решая квадратное уравнение, получаем, что a = 3. Тогда большая сторона будет равна 6.
(a + 3) = 18, получаем a2 + 3a − 18 = 0, решая квадратное уравнение, получаем, что a = 3. Тогда большая сторона будет равна 6.
Ответ: 6.
B 3 № 27602. Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1:2.
Решение.
Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, тогда вторая равна 2a. Периметр будет соответственно равен P = 2  a + 2
a + 2  2a = 18, тогда одна из сторон равна 3, а другая 6. Поэтому S = 3
2a = 18, тогда одна из сторон равна 3, а другая 6. Поэтому S = 3  6 = 18.
6 = 18.
Ответ: 18.
|
| B 3 № 27603. Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.
Решение. Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, тогда вторая равна 2a. Площадь прямоугольника будет соответственно равна S = 2a2 = 18, тогда одна из сторон равна 3, а другая 6. Поэтому P = 2  3 + 2 3 + 2  6 = 18. 6 = 18. Ответ: 18. |
B 3 № 27707. Две стороны прямоугольника  равны 6 и 8. Найдите длину вектора
равны 6 и 8. Найдите длину вектора  .
.
ешение.
Вектор  образует в прямоугольнике два прямоугольных треугольника. Поэтому по теореме Пифагора
образует в прямоугольнике два прямоугольных треугольника. Поэтому по теореме Пифагора
Ответ: 10.
B 3 № 27811. Найдите диагональ прямоугольника, две стороны которого равны  и
и  .
.
Решение.
по теореме Пифагора диагональ равна .
Ответ: 10.
B 3 № 27814. Найдите сторону квадрата, диагональ которого равна  .
.
Решение.
По теореме Пифагора , значит,
.
Ответ: 2.
Ромб
|
| B 3 № 27614. Найдите площадь ромба, если его диагонали равны 4 и 12. Решение. Площадь ромба равна половине произведения его диагоналей. Поэтому . Ответ: 24. |
B 3 № 27615. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
Решение.
Площадь ромба равна половине произведения его диагоналей, следовательно,
,
где a — искомая диагональ. Поэтому a = 3.
Ответ: 3.
B 3 № 27615. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
Решение.
Площадь ромба равна половине произведения его диагоналей, следовательно,
,
где a — искомая диагональ. Поэтому a = 3.
Ответ: 3.
B 3 № 27616. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
Решение.
Площадь ромба равна половине произведения его диагоналей. Пусть меньшая из диагоналей равна a, тогда большая равна 3a. Следовательно,
.
Поэтому  .
.
Ответ: 2.
B 3 № 27713. Диагонали ромба  равны 12 и 16. Найдите длину вектора
равны 12 и 16. Найдите длину вектора  .
.
Решение.Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам. Тогда вектор  является гипотенузой в прямоугольном треугольнике. По теореме Пифагора получаем, что .
является гипотенузой в прямоугольном треугольнике. По теореме Пифагора получаем, что .
Ответ: 10.
|
| B 3 № 27717. Диагонали ромба  пересекаются в точке пересекаются в точке  и равны 12 и 16. Найдите длину вектора и равны 12 и 16. Найдите длину вектора  + +  . .
Решение. Сумма векторов + +  равна вектору равна вектору  . .  — ромб, его диагонали пересекаются под прямым углом, значит, — ромб, его диагонали пересекаются под прямым углом, значит, . Ответ: 10. |
B 3 № 27718. Диагонали ромба  пересекаются в точке
пересекаются в точке  и равны 12 и 16. Найдите длину вектора .
и равны 12 и 16. Найдите длину вектора .
Решение.
Разность векторов  и
и  равна вектору
равна вектору  . Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам. Тогда вектор
. Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам. Тогда вектор  является гипотенузой в прямоугольном треугольнике. По теореме Пифагора получаем, что .
является гипотенузой в прямоугольном треугольнике. По теореме Пифагора получаем, что .
Ответ: 10.
Треугольник
B 3 № 27543.
На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.

|
| B 3 № 27544. На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.

|
B 3 № 27545. На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
 .
.
B 3 № 27547. На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.

B 3 № 27548. На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.

B 3 № 27549. На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.

|
| B 3 № 27617. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10. 
|
B 3 № 27623. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?

Прямоугольник
B 3 № 27550. На клетчатой бумаге с клетками размером 1 см  1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.

|
| B 3 № 27551. Найдите площадь квадрата ABCD, считая стороны квадратных клеток равными 1. |
B 3 № 27584. Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 4 и 9.
|
| B 3 № 27600. Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой.
|
B 3 № 27601. Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны.
B 3 № 27602. Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1:2.
|
| B 3 № 27603. Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.
|
B 3 № 27707. Две стороны прямоугольника  равны 6 и 8. Найдите длину вектора
равны 6 и 8. Найдите длину вектора  .
.
B 3 № 27811. Найдите диагональ прямоугольника, две стороны которого равны  и
и  .
.
B 3 № 27814. Найдите сторону квадрата, диагональ которого равна  .
.
Ромб
|
| B 3 № 27614. Найдите площадь ромба, если его диагонали равны 4 и 12.
|
B 3 № 27615. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
B 3 № 27615. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
B 3 № 27616. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
B 3 № 27713. Диагонали ромба  равны 12 и 16. Найдите длину вектора
равны 12 и 16. Найдите длину вектора  .
.
|
| B 3 № 27717. Диагонали ромба  пересекаются в точке пересекаются в точке  и равны 12 и 16. Найдите длину вектора и равны 12 и 16. Найдите длину вектора  + +  . . |
B 3 № 27718. Диагонали ромба  пересекаются в точке
пересекаются в точке  и равны 12 и 16. Найдите длину вектора .
и равны 12 и 16. Найдите длину вектора .
B 3 № 27811. Найдите диагональ прямоугольника, две стороны которого равны  и
и  .
.
B 3 № 27814. Найдите сторону квадрата, диагональ которого равна  .
.
Ромб
|
| B 3 № 27614. Найдите площадь ромба, если его диагонали равны 4 и 12.
|
B 3 № 27615. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
B 3 № 27615. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
B 3 № 27616. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
B 3 № 27713. Диагонали ромба  равны 12 и 16. Найдите длину вектора
равны 12 и 16. Найдите длину вектора  .
.
|
| B 3 № 27717. Диагонали ромба  пересекаются в точке пересекаются в точке  и равны 12 и 16. Найдите длину вектора и равны 12 и 16. Найдите длину вектора  + +  . . |
B 3 № 27718. Диагонали ромба  пересекаются в точке
пересекаются в точке  и равны 12 и 16. Найдите длину вектора .
и равны 12 и 16. Найдите длину вектора .

 Получите свидетельство
Получите свидетельство Вход
Вход








 Площадь треугольника равна разности площади прямоугольника и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому
Площадь треугольника равна разности площади прямоугольника и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому
 Площадь треугольника равна разности площади большого квадрата, маленького квадрата и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому
Площадь треугольника равна разности площади большого квадрата, маленького квадрата и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому











 Карточки по геометрии на тему "Нахождение площадей на клетчатой бумаге" (0.24 MB)
Карточки по геометрии на тему "Нахождение площадей на клетчатой бумаге" (0.24 MB)
 0
0 2657
2657 374
374 Нравится
0
Нравится
0


