учитель Тучина А. Ю.
Цели урока:
Образовательные: (развивающие - в интеграции предметов)
Дать понятие правильных многогранников, выяснить сколько их существует, каковы их названия, и где они применяются. Осуществить связь между новым материалом, ранее изученным и изучаемым в дальнейшем. Показать межпредметные связи.
Развивающие: Проверить ЗУН учащихся при работе с компьютерной программой (умение копировать рисунок; делать надпись соответствующего размера, шрифта, цвета; настраивать анимацию выделенных объектов, звуковые эффекты; осуществлять переход от одного слайда к другому, работать с определёнными программами и панелью задач.)
Воспитательные: Всесторонне способствовать развитию устойчивого интереса к математике через обучение с применением информационных технологий.
Задачи:
1. Выявить уровень подготовленности учащихся по информатике и геометрии; систематизировать полученные знания. Использовать программу DG –геометрия
2. Помочь в развитии и саморазвитии творческих способностей личности; обучить приёмам организации интеллектуального труда.
3. Научить учащихся ориентироваться в мировом океане информации, умению отбирать нужную информацию.
4. Сформировать понятие правильного многогранника, научить выявлять по существенным признакам правильные многогранники среди массы многогранников других типов.
5. Продолжить воспитание у учащихся уважительного отношения друг к другу, чувства товарищества, культуры общения, чувства ответственности, аккуратности (при оформлении заданий), эстетичности (при работе со слайдами).
Структура урока:
1 этап - организационный (вступительное слово учителя 3-5 мин).
2 этап - усвоение нового материала (работа с презентацией и объяснение материала учителем 30-35 мин + физкультминутка).
3 этап - закрепление новых знаний.
4 этап - самостоятельная практическая работа (с презентацией 5-8 мин )
5 этап - 6 этап - подведение итогов урока (2-3 мин).
7 этап - задание на дом (2-3 мин).
Актуальность: Интегрированные уроки с использованием новых компьютерных технологий позволяют повысить мотивацию учащихся в изучении предметов не только естественно-математического цикла, также позволяют активизировать их познавательную деятельность, формировать общее мировоззрение на современном научном уровне.
Данный урок актуален тем, что "работает" на последующие уроки, темы, разделы. На следующем уроке геометрии планируется решение задач на нахождение площадей сечений правильных многогранников, на зачёте по теме "Многогранники" в теоретической части есть вопрос: “Какие многогранники называются правильными? Сколько их существует? И что о них вы можете рассказать?”. Во втором полугодии изучается тема "Объёмы многогранников", где учащиеся должны научиться находить объёмы не только произвольных, но и правильных многогранников. В конце учебного года данный материал используется при решении задач по теме "Комбинации геометрических тел". Кроме того, данный урок не только способствует развитию устойчивого интереса к математике, но и выполняет ряд воспитательных задач, направленных на развитие личности ребёнка.
Оборудование:
компьютерный класс;
для каждой пары учеников, сидящих за одним компьютером - модели пяти правильных многогранников и одного звёздчатого тела (для выполнения десятого практического задания);
на доске - высказывание Бертрана Рассела, тема урока, чертежи для понятия выпуклых многоугольников и многогранников; химические формулы природных кристаллов, имеющих форму правильных многогранников;
плакаты, выражающие дуальность куба и октаэдра, икосаэдра и додекаэдра; наглядные пособия, позволяющие выявить количество правильных многогранников (с изображениями-макетами многогранных углов);
рабочие карты учащихся;
творческие работы учеников;
модели звёдчатых многогранников;
карточки с вопросами практической части;
тесты для домашней работы.
ХОД УРОКА
Слайд 1: (вступительное слово учителя) - Добрый день, ребята! Добрый день, уважаемые коллеги! Я хочу пригласить Вас в удивительно- сказочный мир под названием “Мир многогранников".
Е сть в школьной геометрии особые темы, которые ждешь с нетерпением, предвкушая встречу с невероятно красивым материалом. К таким темам можно отнести "Правильные многогранники".
сть в школьной геометрии особые темы, которые ждешь с нетерпением, предвкушая встречу с невероятно красивым материалом. К таким темам можно отнести "Правильные многогранники".
Здесь не только открывается удивительный мир геометрических тел, обладающих неповторимыми свойствами, но и интересные историко-философские концепции, оригинальные научные гипотезы. И тогда урок геометрии становится своеобразным исследованием неожиданных сторон привычного школьного предмета.
Ни одни геометрические тела не обладают таким совершенством и красотой , как правильные многогранники.
"Правильных многогранников вызывающе мало, -написал когда-то Л.Кэролл, - но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук".
Слайд 2,3,:- Сегодня на уроке мы узнаем и увидим много интересного, познакомимся с некоторыми видами многогранников, в частности, с правильными многогранниками; нам предстоит ответить на такие вопросы, как, например: Какие многогранники называются правильными? Сколько их существует? Что такое Эйлерова характеристика? Какие тела носят название тел Кеплера- Пуансо? И многие- многие другие… И, наконец: где, зачем и для чего нам нужны многогранники? Может быть, в жизни можно обойтись и без них? Данный материал пригодится нам при изучении темы “Объемы многогранников и при решении задач на комбинацию геометрических тел.
Урок у нас сегодня необычный. Во-первых, это одновременно и урок геометрии, и урок информатики. Поэтому после изучения новой темы вам предстоит выполнить небольшую практическую работу, на которой вы должны проявить свои познания в области информатики при работе с программой Microsoft Power Point. Во-вторых, работать на уроке вы будете в парах, поэтому оценка, которая будет выставлена вашей паре по окончании урока, во многом будет зависеть от работоспособности каждого из вас.
Слайд 4: Итак, я приглашаю вас в “Мир многогранников”. Мне хотелось бы начать со слов Бертрана Рассела: “Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства”.
Многогранники представляют собой простейшие тела в пространстве, подобно тому, как многоугольники – простейшие фигуры на плоскости. С какими многогранниками мы уже знакомы?
Слайд 5:…Вспомнить понятие выпуклого многоугольника, по аналогии дать понятие выпуклого многогранника.

Слайд 6:Правило выпуклого многогранника записали в тетрадь.
Слайд 7:Определение правильного многогранника. ( запись в тетрадь) Проговорить название многогранников
Слайд 8,9:Откуда взялось понятие « правильный» . Название “правильные” идет от античных времен, когда стремились найти гармонию, правильность, совершенство в природе и человеке. Правильные многоугольники – это многоугольники, у которых все стороны и все углы равны, правильные многогранники – это многогранники, ограниченные правильными и одинаковыми многоугольниками.
До сих пор многоугольники нередко называют в науке по-гречески с окончанием “гон”: полигон – многоугольник, пентагон – пятиугольник (такой формы сверху здание Театра Российской Армии в Москве и Министерства обороны США в Вашингтоне), гексагон – шестиугольник (ячейка пчелиных сот сверху) и т.д.
Каждый из вас знаком с простейшими пространственными математическими фигурами, или многогранниками. По- гречески они оканчиваются на “эдр”. Тетраэдр напоминает пирамиду или треугольный пакет для молока или майонеза; куб, или гексаэдр – это известный всем с раннего детства кубик и т.д.
Слайды 10: Все правильные многогранники были известны еще в Древней Греции, и им посвящена заключительная, 13-я книга знаменитых “Начал” Евклида. Как говорилось раньше, эти многогранники часто называют также платоновыми телами – в идеалистической картине мира, данной великим древнегреческим мыслителем Платоном, четыре из них олицетворяли 4 стихии: тетраэдр – огонь, куб – землю, икосаэдр – воду, октаэдр – воздух, пятый же многогранник, додекаэдр, символизировал все мироздание – его по-латыни стали называть quinta essentia (квинта эссенция), означающее все самое главное, основное, истинную сущность чего-либо.
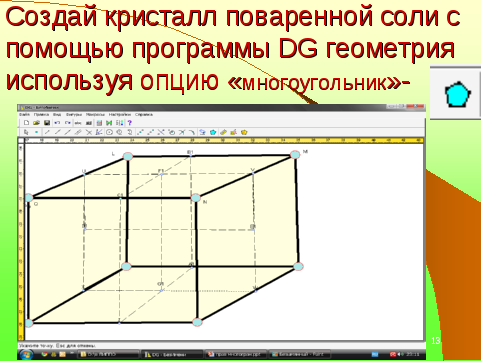
Слайд 11,12: Прочитаем дополнительный материал. Придумать правильный тетраэдр, куб, октаэдр, по-видимому было нетрудно, тем более, что эти формы имеют природные кристаллы, например: форму куба имеет монокристалл поваренной соли (NaCl), форму октаэдра – монокристалл алюмокалиевых квасцов ((KAlSO4)2*12H2O). Существует предположение, что форму додекаэдра древние греки получили, рассматривая кристаллы пирита (сернистого колчедана FeS) и т.д
Слайды 13: Используя программу DG –геометрия создать многогранник ( тренировочная, обучающая работа в программе.
Слайды 14-19: Перед вами пять моделей правильных многогранников. Познакомьтесь с ними.
Слайд 20: Заполните, пожалуйста, таблицу в вашей рабочей карте (подсчитайте количество вершин, граней и ребер у правильных многогранников.). Выполни работу используя DG –геометрия 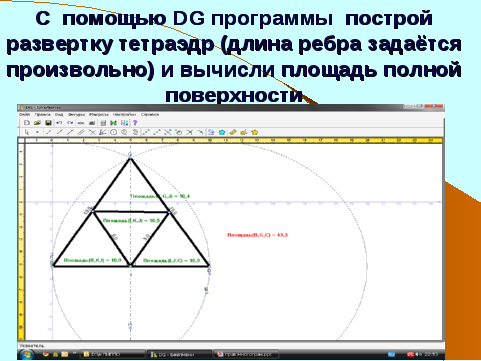
Слайд 21: Для любого выпуклого многогранника справедлива формула Эйлера, устанавливающая связь между числом вершин, граней и ребер. В – Р + Г = 2 . Давайте проверим правильность заполнения вами таблицы и выполнение данной формулы.
| Многогранник | Число сторон грани, m | Число граней, сходящихся в вершине, n | Число плоских углов при одной вершине
| Число плоских углов на поверхности
| Сумма плоских углов при одной вершине | Число вершин В | Число ребер Р | Число граней Г |
|
|
| Тетраэдр | 3 | 3 |
| 12 |
| 4 | 6 | 4 |
|
|
| Гексаэдр (куб) | 4 | 3 |
| 24 |
| 8 | 12 | 6 |
|
|
| Октаэдр | 3 | 4 |
| 24 |
| 6 | 12 | 8 |
|
|
| Икосаэдр | 3 | 5 |
| 60 |
| 12 | 30 | 20 |
|
|
| Додекаэдр | 5 | 3 |
| 60 |
| 20 | 30 | 12 |
|
|
(учащиеся вслух проговаривают названия правильных многогранников)
Слайд 22: Таблица с ответами
Слайд 23: Вывод: Мы убедились, что существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями.
Слайд 24:Физкультминутка
Слайд 25: Попробуем классифицировать многогранники. Что нам известно из это схемы?
Слайд 26:Ещё раз посмотрим на 5 правильных многогранников и вместе повторим их названия.
Слайд 27:Следующий вид многогранников – тела Архимеда.
Чем же они отличаются от Платоновых тел? (Грани – правильные многоугольники нескольких типов)
Слайд 28: Множество Архимедовых тел можно разбить на несколько групп
Одну из них составляют пять многогранников, которые получаются из Платоновых тел в результате их усечения. Усеченное тело – это тело с отрезанной верхушкой. Для Платоновых тел усечение может быть сделано таким образом, что и получающиеся новые грани и остающиеся части старых будут правильными многоугольниками. К примеру, тетраэдр (можно усечь так, что его четыре треугольные грани превратятся в четыре гексагональные, и к ним добавятся четыре правильные треугольные грани.
Таким путем могут быть получены пять Архимедовых тел: усеченный тетраэдр, усеченный гексаэдр (куб), усеченный октаэдр, усеченный додекаэдр и усеченный икосаэдр
Слайды 29: Архимедовы тела обладают свойством: любые две вершины можно совместить так, что все грани многогранника попарно совпадут друг с другом.
Многогранник на рисунке в центре этим свойством не обладает. Древние греки обладали высокоразвитым чувством гармонии и не удивительно, что этот многогранник не попал в число архимедовых тел. В течение двух тысячелетий он находился в “тени” и был “изобретен” в середине 20 столетия независимо несколькими математиками в разных странах. В нашей литературе этот многогранник часто называют телом Ашкинузе, по имени советского математика, который первым обратил на него внимание.
Закрепим изучение темы выполнением задания 3 и 4
Слайды 30: Рассмотрим теперь примеры невыпуклых тел: Тела Кеплера – Пуансо
Среди невыпуклых однородных многогранников существуют аналоги Платоновых тел - четыре правильных невыпуклых однородных многогранника или тела Кеплера - Пуансо.
Как следует из их названия, тела Кеплера-Пуансо - это невыпуклые однородные многогранники, все грани которых - одинаковые правильные многоугольники, и все многогранные углы которых равны. Грани при этом могут быть как выпуклыми, так и невыпуклыми.
Слайды 31:
звездчатые многогранники, которые в отличие от Платоновых и Архимедовых тел являются правильными выпуклыми многогранниками. В начале прошлого столетия французский математик и механик Л. Пуансо (1777-1859), геометрические работы которого относятся к звездчатым многогранникам, в развитие работ Кеплера открыл существование еще двух видов правильных невыпуклых многогранников. Итак, благодаря работам Кеплера и Пуансо стали известными четыре типа таких фигур в 1812 г.
Правильные звездчатые многогранники (тела Пуансо)
Может возникнуть вопрос: «А зачем вообще изучать правильные многогранники? Какая от них польза?». На этот вопрос можно ответить: «А какова польза от музыки или поэзии? Разве все красивое полезно?». Модели многогранников, приведенные, прежде всего, производят на нас эстетическое впечатление и могут использоваться в качестве декоративных украшений. Но на самом деле широкое проявление правильных многогранников в природных структурах послужило причиной огромного интереса к этому разделу геометрии в современной науке
Большой вклад в развитие теории многогранников внес Иоганн Кеплер (1571-1630). В свое время он написал этюд «О снежинке», в котором высказал такое замечание: «Среди правильных тел самое первое, начало и прародитель остальных – куб, а его, если позволительно так сказать, супруга – октаэдр, ибо у октаэдра столько углов, сколько у куба граней». Кеплер первым опубликовал полный список тринадцати Архимедовых тел и дал им те названия, под которыми они известны поныне.
Слайды 32:Ещё раз посмотрим на 4 фигуры Кеплера и вместе повторим их названия.
Слайды 33 -39:Знакомимся самостоятельно. Обсуждаем кому что понравилось.
Слайды 40:Домашнее задание
Слайды 41:Урок закончен! Математики шутят. Забавная математика?!
- 5 -

 Получите свидетельство
Получите свидетельство Вход
Вход












 Изучение правильных многогранников с использованием программы "DG - геометрия" (280.5 KB)
Изучение правильных многогранников с использованием программы "DG - геометрия" (280.5 KB)
 0
0 394
394 11
11 Нравится
0
Нравится
0


