Измерение информации

Измерение информации. Содержательный подход

Информативность сообщения характеризуется содержащейся в нём полезной информацией — той частью сообщения, которая снимает полностью или уменьшает неопределённость какой-либо ситуации.

Клод Шеннон

1916 – 2001 гг.

Является основателем теории информации, нашедшей применение в современных высокотехнологических системах связи.

Внёс огромный вклад в теорию вероятностных схем, теорию автоматов и теорию систем управления — области наук, входящие в понятие «кибернетика» .

В 1948 г. предложил использовать слово «бит» для обозначения наименьшей единицы информации.

Клод Шеннон

1916 – 2001 гг.

Нет информации

Есть информация

Количество информации не равно нулю

Количество информации равно нулю

Сообщение, уменьшающее неопределённость знаний в два раза, несёт 1 бит информации .

Зачёт?

Незачёт?

Информационное сообщение об оценке за зачёт приводит к уменьшению неопределённости знания в два раза, так как получено одно из двух возможных информационных сообщений.

2

3

5

4

Информационное сообщение

об оценке за контрольную работу приводит к уменьшению неопределённости знания в четыре раза, так как получено одно из четырёх возможных информационных сообщений.

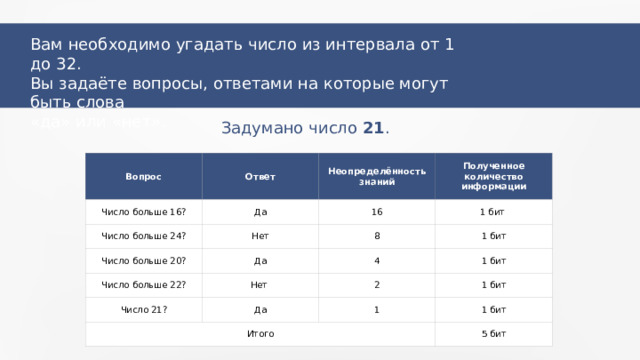
Вам необходимо угадать число из интервала от 1 до 32.

Вы задаёте вопросы, ответами на которые могут быть слова

«да» или «нет».

На каждом шаге в два раза уменьшать неопределённость знаний, т.е. задавать вопросы, делящие числовой интервал на 2.

Ответ «да» или «нет» будет содержать 1 бит информации. Подсчитав общее количество битов (ответов на вопросы), найдём количество информации, необходимое для отгадывания числа.

Вам необходимо угадать число из интервала от 1 до 32.

Вы задаёте вопросы, ответами на которые могут быть слова

«да» или «нет».

Задумано число 21 .

Вопрос

Ответ

Число больше 16?

Да

Число больше 24?

Неопределённость знаний

Число больше 20?

Нет

16

Полученное количество информации

1 бит

Да

8

Число больше 22?

Число 21?

Нет

1 бит

4

1 бит

Да

2

Итого

1 бит

1

1 бит

5 бит

Зачёт — незачёт

2 3 4 5

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

— количество возможных результатов или неопределённость знаний.

— количество информации в сообщении о том, что произошло одно из N событий.

Таблица степени 2

I , битов информации

N , вариантов

1

2

2

3

4

8

4

5

16

6

32

7

64

128

8

9

256

512

10

1024

6 вариантов – между 4 (2 бита) и 8 (3 бита)

Ответ : количество информации между

2 и 3 битами

!

Количество информации может быть нецелым числом!

1 байт = 8 битов

12

Количество информации зависит не только от возможных вариантов исхода события, но и от вероятности получения ответа.

Причём чем больше вероятность события, тем меньшее количество информации в сообщении о таком событии. Вероятность — ожидаемость события. Она измеряется

в долях (от 0 до 1) или в процентах.

Вы выходите на следующей остановке?

Да.

N = 2

N = 2 i

2 i = 2

i = 1

В корзине лежат 8 шаров, все разного цвета. Найти количество информации в сообщении о том, что наугад вынули красный шар.

Решение :

Количество шаров разного цвета в корзине, а значит и количество возможных событий при вытаскивании одного шара: N = 8.

Вычисляем количество информации о том, что вытянули шар красного цвета:

i = log 2 N = log 2

8 = 3 бита.

N = 8

N = 8 i

8 i = 3

i = 3

12

Предположим, в книжном шкафу восемь полок. Книга может быть поставлена на любую из них. Сколько бит информации несёт сообщение о том, что книга поставлена на третью полку?

i= log2 N = log2

8 = 3 бита

В коробке 16 карандашей разного цвета. Сколько бит информации несет сообщение о том, что достали синий карандаш?

Решение:

i= log2 N = log2

16 = 4 бита

N = 16

N = 2 i

2 i = 16

i = 4

Сообщение о том, что ваш знакомый живёт на 5 этаже,

несёт 3 бита информации. Сколько этажей в доме?

i =3

N = 2 i

2 3 = 8

N = 8

Вероятностный подход при измерении информации

Пусть в результате испытания наступило некоторое событие. Вероятность его наступления можно вычислить по формуле:

где N – количество всех возможных исходов испытания,

K – количество исходов испытания, удовлетворяющих данному событию.

Количество информации в сообщении о том, что наступило одно из возможных событий, можно вычислить по формуле:

где P – вероятность наступления события,

i – количество информации в сообщении о том, что наступило данное событие.

Вероятностный подход к измерении информации используется для измерения количества информации при разновероятных событиях

В 1948 году американский инженер и математик К Шеннон предложил формулу для вычисления кол-ва информации для событий с различными вероятностями

логарифм по основанию

В корзине лежат 16 шаров: 4 синих и 12 красных. Найти количество информации в сообщении о том, что из корзины наугад вынули синий шар.

Решение:

Общее количество шаров в корзине: N = 16.

Количество шаров синего цвета: K = 4.

Вероятность того, что из корзины наугад вынули синий шар может быть рассчитана по формуле:

P = K  /   N ;

P = 4   /   16 = 1   /   4.

Тогда количество информации в сообщении об этом событии:

i = log 2   (1   /   P );

i = log 2  4 = 2 ( бита ) .

логарифм по основанию 2

i = log 2   (1   /   P );

16/4=4 – следовательно ответ 2 бита

В сообщении о результатах некоторого события можно измерить количество информации.

События, о которых сообщается, могут быть равновероятными и не равновероятными.

1 бит — количество информации в сообщении об одном из двух равновероятных результатов события.

Главная формула информатики N = 2 i , где N — неопределённость знания, т.е. число возможных вариантов сообщения, i — количество информации в сообщении об одном результате события.

02.02.22