Утверждаю
Директор МОУ «УСОШ с УИОП»
________________________________/Лобанова Г.И./
Приказ № _______________________
От «______»_____________________20_____г.
Программа элективного курса по математике
«Избранные вопросы математики»
в 9 классе
Направление: общеинтеллектуальное
Составитель: Усачёва А.О.
учитель математики высшей квалификационной
категории
Срок реализации 2014-2015 учебный год
Содержание
Пояснительная записка…………………………………………………………………….….3
Предполагаемые результаты……………………………………………………………....5
Тематическое планирование...…………………………………………………………....6
Содержание курса………………………………………..………………………………………6
Перечень учебно – методического и материально – технического, информационного обеспечения…………………………………………………………12
Литература………………………………………………………………………………………..…14
Пояснительная записка
Цели обучения математике в общеобразовательной школе определяются её ролью развитии общества в целом и в развитии интеллекта, формировании личности каждого человека. Известно , что человеку в его практической деятельности приходится решать не только неоднократно повторяющиеся задачи, но и новые в нестандартных условиях. Необходимо учиться находить пути к решению проблем. Развивать творческое мышление учащихся, делать «крупицы открытий» позволяет урочная и внеурочная деятельность по математике. Они создают условия для развития интеллекта и креативности каждого ученика. Чтобы выполнить задания, ученик должен не только и не столько знать программный материал, сколько уметь делать выводы на основе сравнений, выявлять закономерности, уметь воображать.
Актуальность программы определена тем, что учащиеся должны иметь мотивацию к обучению математике, стремиться развивать свои интеллектуальные возможности.
В основу программы положены требования Федерального государственного стандарта. Нормативно – правовая база:
- Федеральный закон РФ № 273-ФЗ от 29.12.2012 «Об образовании в Российской Федерации».
-Примерная основная образовательная программа образовательного учреждения. Основная школа, 2011г.
-Приказ Министерства образования и науки Российской Федерации от 30.08.2013г. «Об утверждении Порядка организации и осуществления образовательной деятельности по основным общеобразовательным программам начального общего, основного общего и среднего общего образования».
-Постановление Главного государственного санитарного врача РФ от 29.12 2010г. № 189 «Об утверждении СанПин 2.4.2.2821-10 «Санитарно – эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях».
Программа рассчитана на 35 часов (1 час в неделю) в 9 классе. Настоящая программа включает материал, создающий основу математической грамотности, необходимой как тем, кто собирается стать учёным, инженером, экономистом и будет решать принципиальные задачи, связанные с математикой, так и тем, для кого математика не станет сферой непосредственной профессиональной деятельности.
Общая характеристика курса
Сюжетное построение курса имеет целый ряд позитивных особенностей. Учитель может менять порядок тем, рассматривать не все включённые в него вопросы, а отбирать материал по своему усмотрению в соответствии с возможностями и интересами детей, а также временем, отведённым на занятия по математике. Так как сюжеты не связаны между собой, то учащиеся имеют возможность подключаться к занятиям на любом этапе. Важно, что курс является открытым: в нём можно добавлять новые фрагменты, развивать предложенную тематику или заменять какие-либо сюжеты другими. Главное, чтобы они соответствовали описанным характеристикам – были небольшими по объёму, интересными для учащихся, соответствовали возможностям класса. Материал для занятий подобран таким образом, чтобы можно было проиллюстрировать применение математики на практике, показать связь математики с другими областями знаний, познакомить с некоторыми историческими сведениями , подчеркнуть эстетические аспекты изучаемых вопросов.
Цели курса
-овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности;
-интеллектуальное развитие учащихся, формирование качеств мышления;
-формирование представлений о математических идеях и методах;
-формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
Задачи курса
-систематизировать, уточнить, дополнить и расширить знания учащихся, добиваться достижения творческого подхода в обучении.
-способствовать развитию у учащихся поисковой активности, наблюдательности, смекалки.
-развитие общекультурного кругозора учащихся.
Предполагаемые результаты
Основным результатом освоения содержания элективного курса учащимися станет рост мотивации к дальнейшему изучению математики и овладение следующими умениями:
- обще-учебными (внимательно читать текст, находить ответ на вопрос, составлять таблицу, чётко и полно оформлять запись найденного решения, контролировать выполненные действия).
- обще-логическими (выделять главное, проводить анализ, синтез, сравнение, обобщение, делать выводы, правильно формулировать вопросы и т.д.)
- предметными (составление математической модели, постановка к данному условию задачи, овладение основными арифметическими и алгебраическими способами решения задач и др.)
- коммуникативными (принимать участие в совместной деятельности, работать в парах, малых группах, вести диалог с учителем, с товарищами).
Формы и режим занятий
Занятия проводятся один раз в неделю по 45 минут.
Основными формами образовательного процесса являются – фронтальная (работа в коллективе при объяснении нового материала), индивидуальная (учащемуся даётся самостоятельное задание с учётом его возможностей), групповая (разделение на мини-группы для выполнения определённой работы), коллективная в виде диалогов, практических занятий, круглых столов и др.
Основные виды деятельности учащихся
- самостоятельная работа;
- работа в парах, группах;
-знакомство с научно – популярной литературой по изучаемой теме;
Технологии, используемые для реализации программы, основаны на принципе системно – деятельностного подхода в обучении и включают:
- лекционно – семинарскую систему обучения;
- проблемное обучение;
- дифференцированное обучение;
- ИКТ;
- обучение в сотрудничестве.
Тематическое планирование
| № | Тема | Кол-во часов |
| 1 | Знакомство с комбинаторикой | 4 |
| 2 | Процентные вычисления в жизненных ситуациях | 4 |
| 3 | Золотое сечение | 2 |
| 4 | Треугольник Паскаля | 2 |
| 5 | Шифрование и математика | 4 |
| 6 | Диофантовы уравнения | 2 |
| 7 | Применение свойств квадратичной функции | 2 |
| 8 | Неравенства с двумя переменными на координатной плоскости | 4 |
| 9 | Графики уравнений с модулями | 4 |
| 10 | Графики функций вида 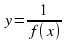 | 2 |
| 11 | Целая и дробная части числа | 2 |
| 12 | Геометрические доказательства теоремы о средних | 3 |
Содержание курса
Знакомство с комбинаторикой (4 ч)
Основная цель – на популярном уровне познакомить с разделом дискретной математики, который приобрел сегодня серьезное значение в связи с развитием теории вероятностей, математической логики, информационных технологий. Учащиеся должны получить представление о том, что такое комбинаторная задача, познакомиться с комбинаторным правилом умножения и систематическим перебором.
Основное содержание
- какую задачу называют комбинаторной. Исторический экскурс.
- решение задач с помощью правила умножения.
- знакомство с другими приёмами.
Процентные вычисления в жизненных ситуациях (4 ч)
Основная цель – показать широту применения в жизни такого простого и известного учащимся математического аппарата, как процентные вычисления.
Основное содержание
- распродажа.
- тарифы.
- штрафы.
- банковские операции.
- голосование.
Золотое сечение (2 ч)
Основная цель – общеобразовательная: знакомство с золотым сечением позволит расширить кругозор учащихся, развить эстетическое восприятие математических фактов, продемонстрировать разнообразие применения математики в реальной жизни.
Основное содержание
- что означают слова «золотое сечение»?
- чему равно золотое сечение?
- строим золотой прямоугольник циркулем и линейкой.
- интересный факт: золотой прямоугольник «сохраняет форму».
- чем привлекает внимание людей пятиконечная звезда?
Треугольник Паскаля. (2 ч)
Основная цель – используя историко-генетический подход, познакомить учащихся с числовой таблицей, называемой треугольником Паскаля; продемонстрировать эффективный приём возведения в произвольную натуральную степень двучлена a + b с использованием этой таблицы.
Основное содержание
- что такое треугольник Паскаля и как его можно «построить».
- некоторые свойства треугольника Паскаля
- введение символических обозначений; задание треугольника Паскаля рекуррентными формулами.
- треугольник Паскаля и возведение в степень двучлена.
Шифрование и математика (4 ч)
Основная цель – на популярном, практически игровом уровне познакомить учащихся с применением математики для решения задач кодирования и декодирования информации. С дидактической точки зрения этот материал эффективен для развития такого важного умения, как выполнение заданного алгоритма.
Основное содержание
- постановка задачи.
- матричный способ шифрования.
- решение задач.
- немного об алгебре матриц.
Диофантовы уравнения (2 ч)
Основная цель – расширить представление учащихся об уравнениях с несколькими переменными, мотивировав и разобрав решение в целых числах. Всё объяснение проводится на примерах, решаются задачи с разнообразными сюжетами, что подчеркивает широту применения рассматриваемых методов.
Основное содержание
- вводная задача и исторический экскурс.
- решение линейных уравнений методом перебора.
- ещё один приём решения – метод «спуска».
- выясняем: всегда ли линейное уравнение с целыми коэффициентами имеет целые решения.
- пример уравнения второй степени решаемого в целых числах (задача о пифагоровых тройках).
Применение свойств квадратичной функции (2 ч)
Основная цель – показать некоторые нестандартные приёмы решения задач на основе свойств квадратичной функции и графических соображений.
Основное содержание
- знаки квадратного трёхчлена вне его корней.
- примеры применения свойств квадратного трёхчлена при решении задач.
- задачи для самостоятельного решения.
Неравенства с двумя переменными на координатной плоскости (4 ч)
Основная цель – расширить представления учащихся о взаимосвязи между алгебраическими соотношениями и их геометрическими образами на координатной плоскости. Необходимо использовать рассматриваемый материал, безусловно включающий эстетический компонент, для развития интереса к предмету, а также для более глубокого освоения базовых умений. Кроме того, важно, чтобы учащимся были предложены задания, апеллирующие к воображению, фантазии.
Основное содержание
- задание областей на координатной плоскости неравенствами вида 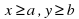 и системой таких неравенств.
и системой таких неравенств.
- задание областей координатной плоскости линейными неравенствами с двумя переменными и системой таких неравенств.
- примеры геометрической интерпретации нелинейных неравенств с двумя переменными и их систем.
Графики уравнений с модулями (4 ч)
Основная цель – познакомить учащихся с основными приёмами построения графиков уравнений, содержащих модули. Привлечь внимание к эстетической стороне данного вида деятельности. Предусмотреть возможность творчества учащихся.
Основное содержание
- подготовительный этап – актуализация базовых знаний и умений. Объяснение и мотивация эстетическими соображениями цели предстоящей работы.
- демонстрация приёмов построения графиков на характерных примерах и выполнение упражнений.
Графики функций вида 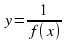 (2 ч)
(2 ч)
Основная цель – показать связь между графиками многочлена 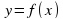 и дробно-рациональной функции
и дробно-рациональной функции 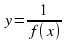 ; исследовать (на наглядном уровне) поведение этой функции при стремлении знаменателя к нулю и при неограниченном (по модулю) возрастании знаменателя.
; исследовать (на наглядном уровне) поведение этой функции при стремлении знаменателя к нулю и при неограниченном (по модулю) возрастании знаменателя.
Основное содержание
- подготовительный этап: постановка цели и проверка базовыми умениями.
- разъяснение приёма на примере графиков функций 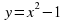 и
и 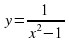 .
.
- упражнения (вариации, дополнительные условия).
- выполнение заданий на готовом чертеже.
Целая и дробная части числа (2 ч)
Основная цель – познакомить учащихся с двумя важными функциями, которые принципиально отличаются от известных им элементарных функций как характером зависимости между переменными, так и графическими изображениями. Это полезное расширение кругозора, противодействие созданию определенных стереотипов.
Основное содержание
- определение целой и дробной частей числа.
- график функции «целая часть числа». Примеры реальных зависимостей.
- график функции «дробная часть числа»
- некоторые более сложные графики.
Геометрические доказательства теоремы о средних (3 ч)
Основная цель – расширить представление учащихся о средних величинах, познакомить их со средним гармоническим 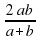 , средним квадратичным
, средним квадратичным 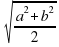 двух положительных чисел и доказать, используя геометрические методы, неравенства:
двух положительных чисел и доказать, используя геометрические методы, неравенства:
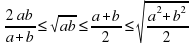 . Материал, предложенный для занятия нельзя назвать популярным в школьной математике, но он интересен и вполне доступен для большинства учащихся, позволяет продемонстрировать единство алгебры и геометрии. Его использование полезно для развития как интереса к математике, так и творческих способностей школьников.
. Материал, предложенный для занятия нельзя назвать популярным в школьной математике, но он интересен и вполне доступен для большинства учащихся, позволяет продемонстрировать единство алгебры и геометрии. Его использование полезно для развития как интереса к математике, так и творческих способностей школьников.
Основное содержание
- историческая справка
- средние: арифметическое, геометрическое, гармоническое, квадратичное.
- доказательства теоремы о средних.
Перечень учебно-методического и материально-технического, информационного обеспечения
Технические средства обучения
1.Мультимедийный комплекс с программным обеспечением
2.Средства телекоммуникации (электронная почта, Интернет)
Печатные пособия
1.Таблицы по математике
2.Портреты выдающихся деятелей математики
Информационно-коммуникативные средства
1. Интерактивный комплекс «Наглядная математика»
2. УМК «Живая математика»
3. Каталог интерактивной медиатеки (ЦОР по математике)
Учебно-практическое и учебно-лабораторное оборудование
1.Доска магнитная
2.Комплект чертежных инструментов
3.Комплекты планиметрических и стереометрических тел (демонстрационных и раздаточных)
Экранно-звуковые пособия
Видеофильмы по истории развития математики, математических идей и методов.
Интернет-ресурсы
http://school-collection.edu.ru− хранилище единой коллекции цифровых образовательных ресурсов, где представлен широкий выбор электронных пособий;
http://www.math.ru−удивительный мир математики/ Коллекция книг, видео-лекций, подборка занимательных математических фактов. Информация об олимпиадах, научных школах по математике. Медиатека;
http://physmatica.narod.ru− «Физматика».Образовательный сайт по физике и математике для школьников, их родителей и педагогов;
http://sbiryukova.narod.ru–Краткая история математики: с древних времен до эпохи Возрождения. Портреты и биографии. События и открытия;
http://www.nt.ru/tp/iz/zs.htm– Золотое сечение. Геометрия золотого сечения: построения и расчеты;
http://www.tmn.fio.ru/works/ – Правильные многогранники: любопытные факты, история, применение. Теорема Эйлера. Платоновы и Архимедовы тела. Биографические сведения о Платоне, Архимеде, Евклиде и других ученых, имеющих отношение к теме. Многогранники в искусстве и архитектуре. Занимательные сведения о некоторых линиях Линии: определения, любопытные факты, примеры использования. Гипербола, парабола, эллипс, синусоида, спираль, циклоида, кардиоида;
http://mathc.chat.ru – Математический калейдоскоп: случаи, фокусы, парадоксы. Математика и математики, математика в жизни. Случаи и биографии, курьезы и открытия;
http://zadachi.yain.net−«Задачи и их решения». Задачи и решения из разных дисциплин, в том числе по математике, программированию, теории вероятностей, логике.
Литература
Акулич И., Бином Ньютона / Энциклопедия для детей. Том 11. Математика.- М.: Аванта плюс, 2002
Болтянский В.Г., Кордемский Б.А. Необыкновенная арифметика / Детская энциклопедия. Изд. 1-е. Т.3.
Виленкин Н.Я., Комбинаторика. – М.: Наука, 1969 и послед. издания.
Гельфанд И.М., Глаголева Е.Г., Шноль Э.Э., Функции и графики. (Серия «Библиотечка физико-математической школы»). – М.: Наука, 1965 (и последующие годы издания).
Гельфонд А.О., Решение уравнений в целых числах (Серия «Популярные лекции по математике»). – М.: Наука 1983г.
Гольдман А.. Звавич Л.И., Числовые средние / Квант. – 1990. - №9
Доморяд А.П., Математические игры и развлечения. – М.: Изд-во физ.-мат. Литературы, 1961.
Дорофеев Г.В., Седова Е.А., Процентные вычисления. Учебное пособие для старшеклассников. – М.: Дрофа, 2008.
Жуков А., Неопределенные уравнения / Энциклопедия для детей. Т. 11. Математика. – М.: Аванта +, 2002.
Искандеров А. геометрические доказательства теорем о средних / Квант. – 1981. №2.
Лэнгдон Н., Снэйт Ч., С математикой в путь. – М,: Педагогика, 1987.
Математика: Алгебра. Функции. Анализ данных. 9кл.: Учебник для общеобразовательных учебных заведений / Г.В. Дорофеев и др. – М.: Дрофа, 2010.
Нечаев В.И., простейшие неопределенные уравнения / Детская энциклопедия. Изд. 1-е. Т. 3; изд. 2-е. Т. 2.
Оре О. Приглашение в теорию чисел // Серия «Библиотечка «Квант»». Вып. 3. –М.: Наука, 1980.
Пичурин Л.Ф. За страницами учебника алгебры: Книга для учащихся 7-9 кл. сред. шк. – М.: Просвещение, 2000.
Пойя Д., Математическое открытие. – М.: Наука, 1976.
Юшкевич А.П. история математики в Средние века. – М.: Физматгиз, 1961.
14


 Получите свидетельство
Получите свидетельство Вход
Вход


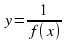
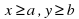 и системой таких неравенств.
и системой таких неравенств.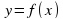 и дробно-рациональной функции
и дробно-рациональной функции 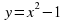 и
и 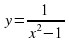 .
.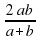 , средним квадратичным
, средним квадратичным 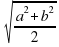 двух положительных чисел и доказать, используя геометрические методы, неравенства:
двух положительных чисел и доказать, используя геометрические методы, неравенства: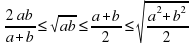 . Материал, предложенный для занятия нельзя назвать популярным в школьной математике, но он интересен и вполне доступен для большинства учащихся, позволяет продемонстрировать единство алгебры и геометрии. Его использование полезно для развития как интереса к математике, так и творческих способностей школьников.
. Материал, предложенный для занятия нельзя назвать популярным в школьной математике, но он интересен и вполне доступен для большинства учащихся, позволяет продемонстрировать единство алгебры и геометрии. Его использование полезно для развития как интереса к математике, так и творческих способностей школьников.








 Избранные вопросы математики (программа элективного курса) (40.69 КB)
Избранные вопросы математики (программа элективного курса) (40.69 КB)
 0
0 589
589 94
94 Нравится
0
Нравится
0




