СПЕЦИФИКАЦИЯ
итоговой диагностической работы по математике
для учащихся 5-х классов общеобразовательных учреждений
1. Назначение диагностической работы
Диагностическая работа проводится в конце учебного года с целью определения уровня подготовки обучающихся 5-х классов общеобразовательных учреждений в рамках мониторинга достижений планируемых результатов освоения основной образовательной программы для образовательных учреждений, участвующих в переходе на ФГОС ООО.
Диагностическая работа охватывает содержание, включенное в массовые учебно-методические комплекты по математике, используемые в 5-х классах.
2. Структура диагностической работы
Работа состоит из 2 частей. Учащиеся на конец учебного года должны продемонстрировать
знания, умения, навыки : складывать, вычитать, делить, умножать десятичные дроби, решать текстовые задачи на нахождение нескольких процентов от числа; находить часть от числа, решать уравнения, решать задачи с помощью уравнений; находить среднее арифметическое нескольких чисел, знать виды углов, знать формулу пути, строить углы заданной градусной меры, решать текстовые задачи на вычисление части угла.
Часть 1 данной работы содержит 9 заданий базового уровня;
Часть 2 данной работы содержит 3 задания повышенного уровня;
Каждый вариант диагностической работы состоит из 12 заданий: шести с выбором одного правильного ответа (ВО), двух заданий с кратким ответом (КО), одного задания на установление соответствия(УС) и трех заданий с развернутым ответом (РО).
В каждом варианте представлены как задания базового уровня сложности, так и задания повышенного уровня сложности
3. Время выполнения работы
На выполнение всей диагностической работы отводится 40 минут.4. Система оценивания отдельных заданий и работы в целом Верное выполнение каждого из заданий 1 – 9 оценивается в 1 балл. Задание 10-12 оценивается 0, 1 или 2 баллами (см. критерии оценивания). Максимальный первичный балл за выполнение всей работы – 15 баллов. Задание с кратким ответом или с выбором ответа считается выполненным, если записанный ответ совпадает с эталоном. Задание с развернутым ответом оценивается экспертом (учителем) с учетом правильности и полноты ответа в соответствии с критериями оценивания. Задание, оцениваемое в 2 балла, считается выполненными верно, если ученик выбрал правильный путь решения и в письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется 2 балла. Если в решении допущена ошибка , не имеющая принципиального характера и не влияющая на общую правильность хода решения, то выставляется 1 балл. 0 баллов получит ученик, если не получен верный ответ и неверный ход рассуждения. За выполнение диагностической работы образовательное учреждение может выставить обучающимся отметки по пятибалльной шкале после выполнения диагностической работы.
Для получения отметки «5» достаточно набрать 11 и более баллов.
Для получения отметки «4» достаточно набрать 8-10 баллов
Для получения отметки «3» достаточно набрать 5-7 баллов
Оценка «2» ставится, если ученик набрал меньше 5 баллов.
| № | Часть работы | Тип заданий | Количество заданий | Максимальный первичный балл |
| 1 | Часть 1 | С кратким ответом в виде одной цифры, которая соответствует номеру правильного ответа | 6 | 1 |
| 2 | Часть 1 | В виде числа, последовательности цифр | 3 | 1 |
| 3 | Часть2 | С развернутым ответом | 3 | 2 |
| ИТОГО |
| 12 | 15 | |
Обобщенный план варианта диагностической работы
| № п/п | Основные проверяемые требования к математической подготовке | Уровень сложности | Максимальный балл | Тип задания |
| 1 | Уметь выполнять деление и вычитание десятичных дробей | Б | 1 | ВО |
| 2 | Уметь располагать десятичные дроби в порядке возрастания | Б | 1 | ВО |
| 3 | Уметь решать задачи с обыкновенными дробями | Б | 1 | ВО |
| 4 | Уметь округлять десятичные дроби. | Б | 1 | ВО |
| 5 | Уметь выполнять умножение и деление дробей на 10, 100, 0,1, 0,001 ит.д. | Б | 1 | КО |
| 6 | Уметь решать уравнение | Б | 1 | ВО |
| 7 | Уметь решать задачу на проценты | Б | 1 | КО |
| 8 | Уметь установить соответствие между рисунком и величиной угла | Б | 1 | УС |
| 9 | Уметь находить среднее арифметическое нескольких чисел | Б | 1 | ВО |
| 10 | Уметь решать задачи на движение | П | 2 | РО |
| 11 | Уметь решать задачи с помощью уравнения | П | 2 | РО |
| 12 | Уметь находить градусную меру угла. | П | 2 | РО |
1 ВАРИАНТ
1. Найдите значение выражения: 0,4 + 1,85 : 0,5
1) 4,5 2) 4,1 3) 3,7 4) 0,77
2. Расположите в порядке возрастания числа: 1,275; 0,128; 1,281; 12,82; 1,027
1) 1,275; 0,128; 1,281; 12,82; 1,027
2) 0,128; 1,281; 1,275; 1,027; 12,82
3) 0,128; 1,027; 1,275; 1,281; 12,82
4) 0,128; 1,275; 1,027; 1,281; 12,82
3. Задача: От веревки длиной 120 см отрезали 1/3 часть. Какова длина оставшейся веревки?
А) 180 см Б) 80 см В) 40 см Г) 60 см
4. Округлите 2,34798 до десятых.
| 1) 2,4 | 2) 2,34 | 3) 2,35 | 4) 2,3 |
5. Выполните умножение и деление
121,39 · 0,01 = ………
17,45 · 1000 = ………
314,51 :100 = ………
0,27 : 0,1 = ……………
6. Решите уравнение : 1,5х+1,2=4,8
| 1) 4 | 2) 50 | 3) 2,4 | 4) 2,04 |
Ответ: …………
7 .Задача. В яблоневом саду собрали 8400 кг яблок. На долю антоновских яблок приходится 45% всего урожая. Сколько килограммов антоновских яблок собрали в саду?
Ответ: …………
8. Установите соответствие.

Ответ: 1…… 2…… 3 ……4 ……
9. На спортивных соревнованиях трое судей оценили выступление гимнаста оценками 5,7; 5,5; 5,6. Найдите среднюю арифметическую оценку гимнаста.
| 1) 5,6 | 2) 5,5 | 3) 5,7 | 4) 5,55 |
Задания №10, №11, №12 решить с записью полного решения.
10. Собственная скорость лодки 5 км/ч, а скорость течения реки 2,2 км/ч. Сначала лодка прошла 1,2 ч против течения, а затем 0,8 ч по течению. Какой путь лодка прошла за всё это время?
11. Решите задачу с помощью уравнения. Два поля занимают площадь 156,8 га. Одно поле на 28,2 га больше другого. Найдите площадь каждого поля.
12. Начертите угол MKN, равный140°. Лучом KP разделите этот угол на два угла так, чтобы угол PKN был равен 55°. Вычислите градусную меру угла MKP.
Вариант 2.
1. Найдите значение выражения: 6,54 – 3,24 : 1,5
1) 2,2 2) 2,16 3) 3,3 4) 4,38
2. Расположите в порядке убывания числа: 1,583; 1,045; 1,451; 0,407; 1,513.
1) 1,583; 1,045; 1,451; 0,407; 1,513
2) 1,583; 1,513; 1,451; 1,045; 0,407
3) 1,513; 1,583; 1,451; 0,407; 1,045
4) 0,407; 1,045; 1,451; 1,513; 1,583
3. Задача :Надо отремонтировать 210 км дороги. В первую неделю отремонтировали 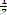 дороги. Сколько километров дороги осталось отремонтировать?
дороги. Сколько километров дороги осталось отремонтировать?
А) 30км Б) 180 км В) 60 км Г) 160 км
4.Округлите 5,24752 до сотых.
| 1) 5,25 | 2) 5,248 | 3) 5,24 | 4) 5,23 |
5. Выполните деление и умножение
87.54 : 10 = …………
87,54 : 0,001 = ………
3,84 * 1000 = ………
0,47 * 0,1 = ………
6. Решите уравнение: 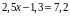 .
.
| 1) 8,5 | 2) 3,4 | 3) 2,36 | 4) 6 |
Ответ: …………
7. Задача .В старших классах 120 учащихся. Из них 85% работали летом на ферме. Сколько учащихся старших классов работали летом на ферме?
Ответ: …………………
8. Установите соответствие.
| 1. 12° | А) тупой угол |
| 2. 91° | Б) острый угол |
| 3. 90° | В) прямой угол |
| 4. 180° | Г) развернутый угол |
Ответ: 1 …… 2 …… 3 …… .4……
9. Купили трёх поросят массой 27,3 кг, 30,5 кг, 18,7 кг. Найдите среднюю массу купленных поросят.
| 1) 27,3 | 2) 25,5 | 3) 30,5 | 4) 38,25 |
Задания №10, №11, №12 решить с записью полного ответа.
10. Лодка шла по течению 0,8 ч и против течения 0,3 ч. Собственная скорость лодки 3,8 км/ч , а скорость течения 1,3 км/ч. Какой путь прошла лодка за это время?
11. Решите задачу с помощью уравнения. Два поля занимают площадь 79,9 га. Площадь первого поля в 2,4 раза больше второго. Какова площадь каждого поля?
12. Начертите угол MOK, равный 155°. Лучом OD разделите этот угол так, чтобы получившийся угол MOD был равен 103°. Вычислите градусную меру угла DOK.
Ответы
| Номер задания | Вариант 1 | Вариант 2 |
| 1 | 2 | 4 |
| 2 | 3 | 2 |
| 3 | 2 | 3 |
| 4 | 1 | 1 |
| 5 | 1,2139, 17450, 3,1415, 2,7 | 8,754, 87540, 3840, 0,047 |
| 6 | 3 | 2 |
| 7 | 3780 | 102 |
| 8 | 1-Б, 2-А, 3-В, 4-Г | 1-Б, 2-А, 3-В, 4-Г |
| 9 | 1 | 2 |
| 10 | 9,12км | 4,83км |
| 11 | 64,3га, 92,5га. | 23,5га, 56,4га. |
| 12 | 85 | 52 |
1 вариант
Решение задачи № 10
5-2,2=2,8(км/ч)- скорость лодки против течения реки.
5+2,2=7,2(км/ч)- скорость лодки по течению реки.
2,8*1,2=3,36 (км) прошла лодка против течения
7,2*0,8=5,76 (км) прошла лодка по течению реки
3,36+5,76=9,12(Км) прошла лодка всего/
Ответ: 9,12км
Решение задачи № 11
х (га)-площадь 1 поля
х+28,2(га)- площадь 2 поля
Два поля занимают площадь 156,8 га.
х+х+28,2=156,8
2х=156,8-28,2
2х=128,6
Х=128,6:2
Х=64,3 (га) площадь 1 поля
Если х=64,3, то 64,3+28,2=92,5(га) площадь 2 поля
Ответ: 64,3га, 92,5га.
Решение задачи № 12
MKP = 140-55= 85
2 вариант
Решение задачи № 10
3,8-1,3=2,5(км/ч)- скорость лодки против течения реки.
3,8+1,3=5,1(км/ч)- скорость лодки по течению реки.
2,5*0,3=0,75 (км) прошла лодка против течения
5,1*0,8=4,08 (км) прошла лодка по течению реки
0,75+4,08=4,83(Км) прошла лодка всего.
Ответ: 4,83км
Решение задачи № 11
х (га)-площадь 1 поля
2,4х (га)- площадь 2 поля
Два поля занимают площадь 79,9 га.
х+2,4х=79,9
3,4х=79,9
х=79,9 :3,4
Х=23,5
Х=23,5 (га) площадь 1 поля
Если х=23,5, то 79,9-23,5=56,4 (га) площадь 2 поля
Ответ: 23,5га, 56,4га.
Решение задачи № 12
DOK = 155-103=52

 Получите свидетельство
Получите свидетельство Вход
Вход











 Итоговая контрольная работа, 5 класс (42.8 KB)
Итоговая контрольная работа, 5 класс (42.8 KB)
 0
0 940
940 75
75 Нравится
0
Нравится
0




