Визитная карточка проекта: «Весь мир – числа»
| Автор проекта | ||||
| Фамилия, имя отчество | Четырина Зоя Владимировна | |||
| Регион | Тамбовская область | |||
| Населенный пункт, в котором находится школа/ОУ | с. Малиновка | |||
| Номер и/или название школы/ОУ | МБОУ «Горельская СОШ», филиал в селе Малиновка | |||
| Описание проекта Часто математика в школе многим из нас дается с трудом, кажется «сухой» и очень сложной. А может быть посмотреть на это с другой, более увлекательной стороны? Тогда и учение станет в радость. Вопрос «Говорят, что числа правят миром. А верно ли это?» является основополагающим для данного проекта. Он рассчитан на учащихся 5-9 классов, родителей и всех неравнодушных к математике как науке, развивающей интеллект, логическое мышление, смекалку, самостоятельность, терпение, силу воли. Работа в проекте коснется как сильных, так и слабых учеников, придав им уверенность в своих силах, ведь этот проект групповой. На протяжении всего времени работы в проекте ребятам представится возможность систематизировать и самостоятельно получить новые знания, применить их к реальной жизни, проверить истинность различных положений, представить оформленные материалы во время защиты работ по окончании проекта. Стимулом к выполнению заданий будет оценивание не только со стороны организатора проекта, но и оценивание внутри группы, а также со стороны товарищей, родителей, гостей при защите работ. | ||||
| Название темы вашего учебного проекта | ||||
| Весь мир - числа | ||||
| Краткое содержание проекта | ||||
| В учебниках по математике в разных местах дается краткая информация о разных видах чисел. Нам захотелось изучить этот вопрос глубже и обобщить все имеющиеся сведения. Число - важнейшее математическое понятие. Проект направлен на знакомство с числами, имеющими особое значение в развитии человечества. | ||||
| Предмет(ы) | ||||
| Искусство, биология, математика | ||||
| Класс(-ы) | ||||
| 7-8 классы | ||||
| Приблизительная продолжительность проекта | ||||
| 2 недели | ||||
| Основа проекта | ||||
| Образовательные стандарты | ||||
| формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов; развитие познавательных интересов, интеллектуальных и творческих способностей; воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса. | ||||
| Дидактические цели / Ожидаемые результаты обучения | ||||
| Дидактические цели проекта: формирование компетентности в сфере самостоятельной познавательной деятельности, формирование навыков самостоятельной работы с большими объемами информации, умение видеть проблему и наметить пути ее решения, формирование критического мышления, навыков работы в команде. воспитание средствами математики культуры личности, воспитание понимания значимости математики для научно-технического прогресса, воспитание отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики. Методические задачи учебного проекта развивать логическое мышление. учить обобщать, систематизировать, анализировать, полученные знания. учить делать выводы. приобрести навыки проектной деятельности. После завершения проекта учащиеся смогут: работать с дополнительными источниками и Интернет-ресурсами (самостоятельно находить нужную информацию, анализировать, обобщать ее и представлять в виде оформленного результата деятельности), знать о наличии закономерностей в природе, описываемых замечательными числами, сформулировать такие качества как: ответственность и адаптивность, межличностное взаимодействие и сотрудничество, креативность и любознательность, критическое и системное мышление. | ||||
| Вопросы, направляющие проект | ||||
| Основополагающий вопрос | Роль чисел в окружающем нас мире | |||
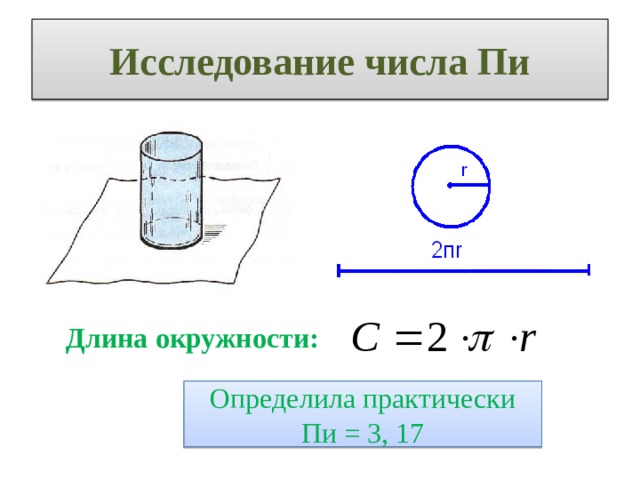
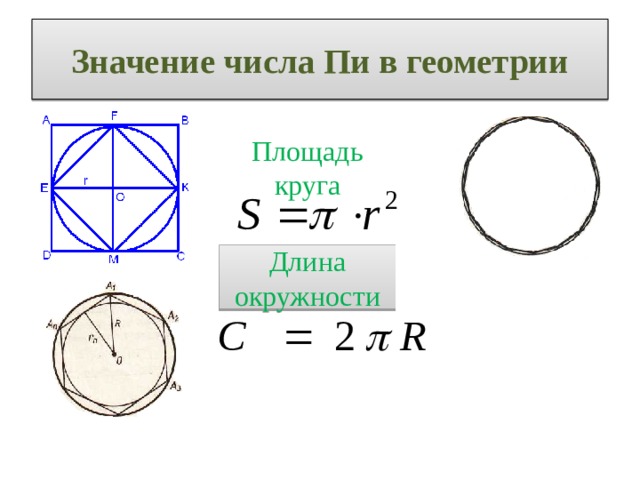
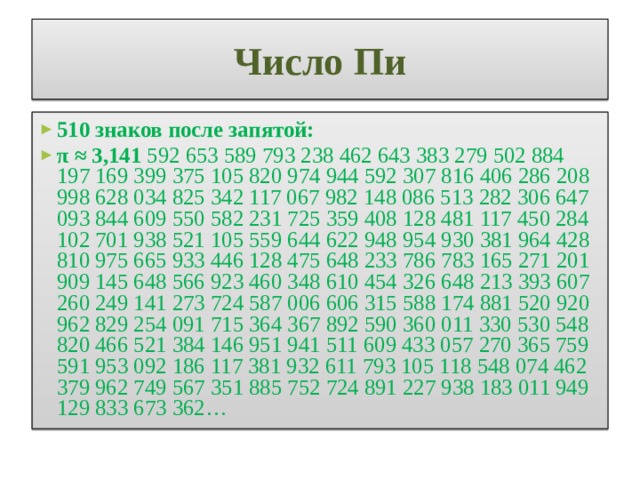
| Проблемные вопросы учебной темы | История возникновения чисел Числа Фибоначчи Число пи | |||
| Учебные вопросы | 1.История возникновения чисел 2.Числа Фибоначчи 2.1.Числа Фибоначчи в природе 2.2.Числа Фибоначчи в искусстве 3.Число пи 3.1.История исследования числа пи 3.2.Число пи в истории развития общества | |||
| План оценивания | ||||
| График оценивания | ||||
| До работы над проектом | Ученики работают над проектом и выполняют задания | После завершения работы над проектом | ||
| Вопросы; обсуждение; составление плана работы; формирование групп; распределение заданий; стартовая презентация учителя; критерии оценивания итогового продукта
| Собирание материала; выявление основных понятий; систематизация собранного; выпуск публикации; создание презентации; критерии самооценки работы в командах. |
Итоговое самооценивание качества работы в команде;
| ||
| Описание методов оценивания | ||||
| Вхождение в проект начинается с повторения сведений о числах, с которыми уже знакомы учащиеся (презентация учителя), объяснения темы и целей проекта, деления учащихся на группы В начале проектной деятельности проводится анкетирование, беседа, далее выполнение собственных проектов и их защита и обсуждение. | ||||
| Сведения о проекте | ||||
| Необходимые начальные знания, умения, навыки | ||||
| Знания курса биологии, искусства, математики на уровне 7 и 9 класса; обработка источников информации и Интернет – ресурсов; | ||||
| Учебные мероприятия | ||||
| 1. Формулирование темы проекта, его целей, задач.
| ||||
| Материалы для дифференцированного обучения | ||||
| Ученик с проблемами усвоения учебного материала (Проблемный ученик) |
Для проблемных учеников будет выделено дополнительное время для занятий. Поставить его под шефство другого, сильного лидера в классе. Поручить посильное задание, в выполнении которого группа верит и ждет результатов. Доброжелательное расположение и внимание, возможность показать ему самому, как много у него положительных качеств, за что его стоит уважать. | |||
| Ученик, для которого язык преподавания не родной |
Нерусскоязычные учащиеся в ходе проекта выполняют доступные задания, четко сформулированные учителем. Они имеют возможность получать индивидуальные консультации, пользоваться помощью других участников, использовать иллюстративные тексты. Эти ребята должны не только почувствовать себя вовлеченными в общую деятельность, но и понять, что они справляются с заданием. | |||
| Одаренный ученик |
Одаренные ученики самостоятельно проводят исследования, приводят доказательства и оформляют свои результаты в виде презентации, веб-сайта и др. Учащиеся этой категории выполняют задания, направленные на | |||
| Материалы и ресурсы, необходимые для проекта | ||||
| Технологии – оборудование (отметьте нужные пункты) | ||||
| Фотоаппарат Лазерный диск Принтер Сканер
| ||||
| Технологии – программное обеспечение (отметьте нужные пункты) | ||||
| Электронные таблицы, программы обработки изображений, текстовые редакторы, программы электронной почты, мультимедийные системы. | ||||
| Материалы на печатной основе | Учебники, методические пособия, хрестоматии, лабораторные пособия, справочный материал и т.д. Босова Л.Л. Информатика: учебник 6 класса, глава «Материал для любознательных» Г.И.Гейзер. История математики в школе. Пособие для учителей. – М.: Просвещение, 1981.. И. Депман. Мир чисел. Рассказы о математике. Ленинград "Детская литература" 1988. И.Я.Депман. Н.Я.Виленкин. За страницами учебника математики. Пособие для учащихся 5-6 классов. Издательство"Просвещение" 1989. Алгебра 9 класс под ред. Макарычева М.Н..Глейзер Г. И. «История математики в школе», М: Просвещение,1982 г. А.Н.Крылов. Числа и меры. Математика/ Прил. К газете "Первое сентября"№7 1994 | |||
| Другие принадлежности |
Журнал «Математика» №8, 1 сентября, с. 48. Кордемский Б.А., Ахадов А.А. «Удивительный мир чисел»: Кн. Для учащихся, - М.: Просвещение, 1986.
| |||
| Интернет-ресурсы | Список веб-адресов, необходимых для проведения проекта http://www.vokrugsveta.ru http://www.posm.ru http://selnov.ru
| |||
| Другие ресурсы | Кого нужно пригласить и что нужно организовать для успешного проведения проекта в процессе (экскурсии, эксперименты, гости, наставники, другие ученики/классы, эксперты, родители и т.д.) Родителей, учителей,администрацию школы. | |||

 Получите свидетельство
Получите свидетельство Вход
Вход

























































 Исследовательская работа "Весь мир числа" (3.35 MB)
Исследовательская работа "Весь мир числа" (3.35 MB)
 0
0 736
736 16
16 Нравится
0
Нравится
0






