Использование свойств планиметрии при решений задач №16 на ЕГЭ по математике

15

Использование свойств планиметрии при решений задач №16 на ЕГЭ по математике

Для многих учеников геометрия (особенно 2 часть) на ЕГЭ вызывает большие опасения, скорее всего из-за широчайшего диапазона взаимосвязей между элементами фигур и их комбинаций. Предмет очень глубокий и требует большего размаха мышления, объемных и систематизированных знаний.

В экзаменационную работу включена планиметрическая задача №16. Она более сложная, чем №14, и при проверке ее выполнения предполагалось более тщательное отношение к доказательной составляющей решения.

В данной статье я решила рассмотреть некоторые свойства многоугольников и их особенности при решении задач, а также показать применение полученных в школе знания на практике.

Цель: систематизация свойства геометрических фигур, их особенностей при решении задач, а также разбор решаний задания ЕГЭ типа №16.

Для достижения поставленной цели были определены следующие задачи:

• изучить учебную и научно-методическую литературу по рассматриваемой проблеме;

• решить геометрические задачи 2 части ЕГЭ;

• систематизировать решённые задачи, выявить те, для решения которых наиболее эффективно применить метод координат, составить алгоритм решения таких задач.

Актуальность исследования: многие учащиеся затрудняются при решении задачи №16 на ЕГЭ, отказываются от решения этих задач.

Новизна: В своей статье я рассмотрела как свойства многоугольников применяются на практике при решении задач №16 из ЕГЭ. Можно сказать, что многоугольник является универсальной фигурой, так как он применяется во многих задачах и обладает множеством интересных свойств. Многоугольники находят своё применение в самых разных науках. Из этого следует ценность многоугольника как фигуры.

Школьный курс геометрии занимает важное место в математическом образовании учащихся. В ходе изучения геометрии у школьников развивается пространственное воображение, логическое мышление. Они приобретают навыки использования линейки, циркуля, прямого угла. Учащиеся убеждаются, что теоретические положения, изучаемые ими, являются отражением реальной действительности и находят отражение в практической деятельности людей.

В курсе геометрии 7-9 классов изучаются геометрические фигуры на плоскости, причём основное внимание уделяется изучению многоугольников и их свойств.

В ходе изучения темы "Многоугольники" вводится много новых понятий, изучаются теоремы, вводятся понятие теоремы обратной данной, решение задач требует от школьника актуализации имеющихся теоретических знаний.

Этот раздел школьного курса геометрии выполняет и определенные мировоззренческие функции.

Многими математическими знаниями люди пользовались уже в глубокой древности – тысячи лет назад. Эти знания были необходимы древним купцам и строителям храмов, дворцов и пирамид, воинам и землемерам, жрецам и путешественникам.

Знания постепенно накапливались и систематизировались. Около 4 тыс. лет назад возникла наука об измерении расстояний, площадей и объёмов, о свойствах различных фигур. Так как речь в основном шла о земельных участках, то древние греки, узнавшие об этой науке от египтян, назвали её геометрией (по-гречески «гео» - земля, а «метрео» - измеряю. Значит, «геометрия» буквально означает «землемерие». Греческие учёные узнали много новых свойств геометрических фигур, и уже тогда геометрией стали называть науку о геометрических фигурах, а для науки об измерении Земли ввели другое название – «геодезия» (происходит от греческих слов «деление земли»).

Древние люди знали, что немаловажное значение имеют такие фигуры как многоугольники. Например, древнегреческие математики (Антифон, Бризон, Архимед и др.) использовали правильные многоугольники для вычисления числа π. Они вычисляли площади вписанных в окружность и описанных вокруг неё многоугольников, постепенно увеличивая число их сторон и получая таким образом оценку площади круга.

Полное правильное решение задачи №16 оценивается 3 баллами. Оценка выполнения задач второй части проводится экспертами на основе специально разработанной системы критериев, базирующейся на следующих требованиях. Метод и форма записи решения могут быть произвольными, но решение должно быть математически грамотным, полным и обоснованным. При этом оцениваются продвижения выпускника в решении задачи. При решении задачи можно использовать без доказательств и ссылок любые математические факты, содержащиеся в учебниках и учебных пособиях, допущенных или рекомендованных Министерством образования и науки РФ.

Гипотезой стала мысль о том, что классификация по видам, классификация свойств, составление задач поможет быстрее научиться решать задачи на ЕГЭ.

Предмет исследования: свойства геометрических фигур при изучении планиметрии.

Исследованием охвачены: программа геометрии 7-9 классов, задачи из экзаменационных тестов ЕГЭ.

• ЕГЭ 2012, Математика, Решение задачи С4, Гордин Р.К.

• ЕГЭ 2013. Математика. Тематические тренировочные задания. Уровень В, С. Лаппо Л.Д., Попов М.А.

• ЕГЭ 2013 Типовые тестовые задания - Под ред. А.Л. Семенова, И.В. Ященко.  — М.: Издательство «Экзамен», 2013.

• Гордин Р. К. ЕГЭ 2011. Математика. Задача С4. Геометрия. Планиметрия / Под ред. А. Л. Семенова и И. В. Ященко. — М.: МЦНМО, 2011.

• Клово А. Г. Математика: интенсивный курс подготовки к ЕГЭ / А. Г. Клово. — Ростов н/Д: Феникс, 2011.

• А так же Интернет ресурсы:

http://nsportal.ru/nachalnaya-shkola/psikhologiya/kak-podgotovitsya-k-vypusknym-ekzamenam

http://reshuege.ru:89/expert?task=4

hthttp://tutor4you.ru/s4.pdf

hthtp://live.mephist.ru/show/mathege-solutions/C4

http://sch273.edusite.ru/DswMedia/agkoryanov-aaprokof-evzadachas4egyematematika2012.pdf

http://webmath.exponenta.ru/ege_11/index_C4.html

Геометрия полна приключений, потому что

за каждой задачей скрывается приключение мысли.

Решить задачу – это значит пережить приключение.

(В. Произволов) 

I. Теоретическая часть

Обучение решению планиметрических задач является одной из важнейших составляющих практики преподавания математики. Задачи используются как материал, способствующий развитию математического мышления, геометрической интуиции, творческой активности учащихся, формированию умения применять теоретические знания на практике.

Задачи С4 по планиметрии вызывают у учащихся наибольшее затруднения и опасения.

Поэтому есть несколько полезных психологических советов учащимся (Приложение 1, стр. I).

Обычно, приступая к решению задачи по планиметрии, учитель предлагает выполнить рисунок аккуратно, с четкими обозначениями, выясняет, что известно и что нужно найти. В процессе выполнения рисунка анализируется условие задачи, устанавливается взаимное расположение отдельных элементов геометрической фигуры и взаимосвязь между этими элементами. Выполнение рисунка требует знания свойств геометрических фигур, умения применять эти свойства на практике.

Если в условии задачи оказывается недостаточно данных для решения, тогда возникает вопрос о выполнении дополнительного построения, которое преобразовало бы условие задачи и направило мысль учащихся в нужном направлении.

Также имеется немало задач, процесс решения которых состоит в последовательном уточнении особенностей рассматриваемой конфигурации с соответствующими переделками и изменениями рисунка, так что окончательный вид рисунок принимает лишь одновременно с окончанием решения.

В данной работе я предлагаю несколько планиметрических задач, детальный анализ которых позволит убедиться в реальной и существенной пользе проделанной работы.

Прежде чем начать разбирать основные типы задач С4, необходимо рассмотреть алгоритм их решения и критерии оценивания (Приложение 2, стр. I)

II. Практическая исследовательская часть

1. Задачи на окружности

Поскольку здесь мы имеем дело с окружностями и ее дугами, то является очевидным использование следующих утверждений:

• если две окружности касаются внешне или внутренне, то точка касания и центры этих окружностей лежат на одной прямой;

• расстояние между центрами двух внешне касающихся окружностей равно сумме радиусов этих окружностей, а расстояние между центрами двух внутренне касающихся окружностей равно разности радиусов большей и меньшей окружностей;

• касательная к окружности или ее дуге перпендикулярна к радиусу окружности или ее дуги, проведенному в точку касания.

• И др. (см. Приложение)

Из всего вышесказанного ясно, что эти задачи окажут учащимся двоякую пользу: во-первых, они получат возможность глубже понять и прочнее усвоить тему «Окружность», во-вторых, эти задачи разовьют у учащихся умение быстро и безошибочно выполнять различные алгебраические действия.

Задача 1.1.

Найдите длину отрезка общей касательной к двум окружностям, заключенного между точками касания, если радиусы окружностей равны 23 и 7, а расстояние между центрами окружностей равно 34.

Решение: пусть центры окружностей- точки О₁ и О₂, а А и В — точки касания. Проведем через точку В прямую, параллельную О₁О₂. Точку пересечения этой прямой с О₁А обозначим К. Треугольник КАВ — прямоугольный.

Возможны два случая расположения окружностей и общей касательной.

Случай 1. Окружности лежат по одну сторону от касательной.

Случай 2. Окружности лежат по разные стороны от касательной.

Обозначим радиусы окружностей R и r, расстояние между центрами окружностей l. В первом случае АК=R-r, во втором случае АК=R+r. Из прямоугольного треугольника КАВ находим:

в первом случае ,

во втором случае .

Ответ: 30 или 16.

Проиллюстрируем сказанное выше на наиболее интересных элементарно геометрических задачах на взаимное расположение окружностей и на взаимное расположение прямой и окружности. Решение ниже рассматриваемых задач, как и большого класса других задач на вычисление сводится к последовательному рассмотрению и решению ряда прямоугольных треугольников, с которыми проще всего иметь дело. Но в рисунках ниже рассматриваемых задач их сразу не видно, поэтому необходимо научиться точно и логично мыслить, видеть, чего в рисунке не достает и какие линии надо провести дополнительно, чтобы можно было создать прямоугольные треугольники и с помощью хорошо известной из школьного курса геометрии теоремы Пифагора составить уравнения, из которых будут найдены искомые величины.

З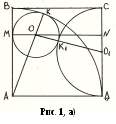адача 1.2.

В квадрате АВСD, сторона которого равна а, из точки А как из центра проведена внутри квадрата дуга через вершины В и D. На стороне DС как на диаметре построена внутри квадрата полуокружность. Найти радиус окружности, касающейся проведенной дуги, полуокружности и одной из сторон квадрата.

Решение:

Поскольку в условии данной задачи конкретно не указано, какой же, именно, сторон квадрата касается искомая окружность, то мы должны рассмотреть три случая, схематически изображенные на рисунке 1(а,б,в).

Случай 1. Рассмотрим сначала случай, когда искомая окружность касается стороне АВ квадрата АВСD (Рис. 1, а)). Обозначим радиус этой окружности через х.

Соединим центр окружности О с центром полуокружности О₁ и с центром дуги А, опустим из центра окружности О перпендикуляры ОМ и ОN на противоположные стороны АВ и СD и рассмотрим полученные при этом построении прямоугольные треугольники.

Из прямоугольного треугольника АМО следует, что неизвестный катет АМ равен, то есть или

Теперь рассмотрим треугольник ОО₁N, в котором гипотенуза

, катет ОN = МN – ОМ = а – х и катет О₁N = DN –D О₁,

где и поэтому

По теореме Пифагора находим OO₁ ² = ОN ² + О₁N ² .

Подставляя найденные выражения для OO₁ , ОN и О₁N в выше написанное уравнение имеем

о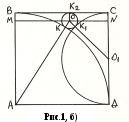ткуда получаем искомый радиус

Случай 2. Пусть теперь искомая окружность касается стороне ВС (Рис. 1, б)). Обозначим радиус этой окружности через у. Сделаем необходимые дополнительные построения и получаем прямоугольные треугольники АОМ и О₁ОN. Из прямоугольного треугольника АОМ по теореме Пифагора найдем катет ОМ.

Он равен

Аналогично найдем из прямоугольного треугольника О₁ОN

к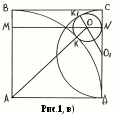атет .

Подставляя найденные значения величин ОМ и ОN в соотношение ВС = ОМ + ОN , получаем . Решая это уравнение, находим

Случай 3. Искомая окружность касается стороне DC (Рис.1, в)).Обозначим радиус этой окружности через z. Опустим из центра О искомой окружности перпендикуляры ОМ и ОN соответственно на стороны АВ и CD квадрата АВСD и соединим центр О с центром полуокружности О₁ и с вершиной А квадрата АВСD . Из полученного при этом построении прямоугольного треугольника ОО₁N по теореме Пифагора имеем .

Следовательно, катет АМ прямоугольного треугольника АМО равен

Из соотношения АO ₂ = АМ ₂ + ОМ ₂ получаем ,

откуда и находится искомый радиус .

Ответ: или , или .

1. Задачи на треугольники

Задача 2.1.

П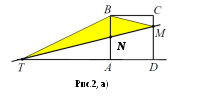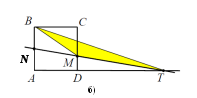рямая, проведенная через середину N стороны AB квадрата ABCD, пересекает прямые CD и AD в точках M и T соответственно и образует с прямой AB угол, тангенс которого равен 4. Найдите площадь треугольника BMT, если сторона квадрата ABCD равна 8.

Решение: Возможны два случая:

Случай 1: точка T лежит на продолжении стороны AD за точку A.

Случай 2: точка T лежит на продолжении стороны AD за точку D.

1) Пусть – угол между прямыми MT и AB.

Рассмотрим первый случай (Рис.2, a)). Заметим, что

S_BMT = S_BNT + S_BMN.

2) AN = 4, поэтому AT = AN*tga = 16. Значит S_BNT =.

Следовательно, S_BMT = 32 +16 = 48.

1) Во втором случае (Рис.2, б)). S_BMT = S_BNT - S_BMN.

2) По-прежнему AT = 16, S_BNT = 32_, S_BMN = 16. Следовательно, S_BMT = 32 -16 = 16.

Ответ: 48 или 16.

1. Задачи на четырехугольники и многоугольники

Задача 3.1.

В параллелограмме ABCD биссектрисы углов при стороне

A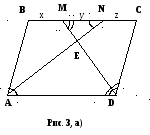D делят сторону BC точками M и N так,

что BM:MN = 1:2.

Найдите BC, если AB=12.

Решение:

Пусть E – точка пересечения биссектрис,

BM = x, MN = y,

NC = z. Так как ,

то точка M лежит между точками B и N.

Возможны два случая.

С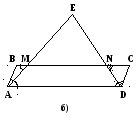лучай 1. Точка E – внутри параллелограмма.

Треугольники ABN и DMC равнобедренные,

, следовательно ; ,

откуда y = 8, z = x = 4, BC= 2x+ y =16.

Случай 2. Точка E – вне параллелограмма.

Тогда x = z = 12, , откуда y=24,

BC= 2x + y = 48.

Ответ: 16 или 48.

Подводя итог, замечу, что ознакомление с предложенными задачами способствует дальнейшему совершенствованию навыков построения и чтения геометрических рисунков и поможет самостоятельно найти решения ряда других, более сложных задач.

Сделаю ещё одно существенное замечание: рассмотрев решение одной-двух задач, изложенных выше, необходимо попытаться решить следующую задачу самостоятельно. Если это не получится, то разобравшись в решении этой задачи, сделать попытку на последующей. Эти попытки не только нужны, но и необходимы, ибо без практики, без тренировки в решении задач С4 невозможно научиться решать аналогичные им задачи.

1. Решение геометрических задач C4 методом координат

Для решения геометрических задач повышенной сложности ЕГЭ во многих случаях можно применить координатный метод, который является наиболее простым и эффективным при решении таких задач. Метод координат не требует больших вычислений, применения различных теорем, сложных дополнительных построений, а также занимает меньше времени, чем традиционные решения задач, что играет немаловажную роль на экзамене. В рамках школьной программы с этим методом знакомятся лишь на базовом уровне, то есть рассматриваются общие теоретические сведения, основные формулы и простые задачи на применение метода координат. Поэтому возникло желание самостоятельно изучить метод координат и рассмотреть решения задач части C ЕГЭ, а именно задачи типа C4, с использованием метода координат. Особенное любопытство вызвало то, что такие задачи можно быстро решать, пользуясь определённым алгоритмом.

З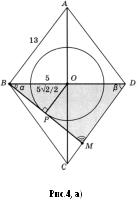адача 4.1.

Дан ромб АВСD с диагоналями АС=24 и ВD=10. Проведена окружность радиусом с центром в точке пересечения диагоналей ромба. Прямая, проходящая через вершину В, касается этой окружности и пересекает прямую CD в точке М. Найдите СМ.

Дано: ABCD – ромб, АС=24 см, BD=10 см, окружность (O;), О – точка пересечения диагоналей и центр окружности, ВМ – касательная к окружности, М Є CD

Найти: СМ

Решение (авторское):

Случай 1.

Пусть точка M лежит между C и D (Рис. 4 а)), P- точка касания прямой BM с данной окружностью, O – центр ромба.

По теореме Пифагора: .

Обозначим . Из прямоугольных треугольников OPB и COD находим, что:

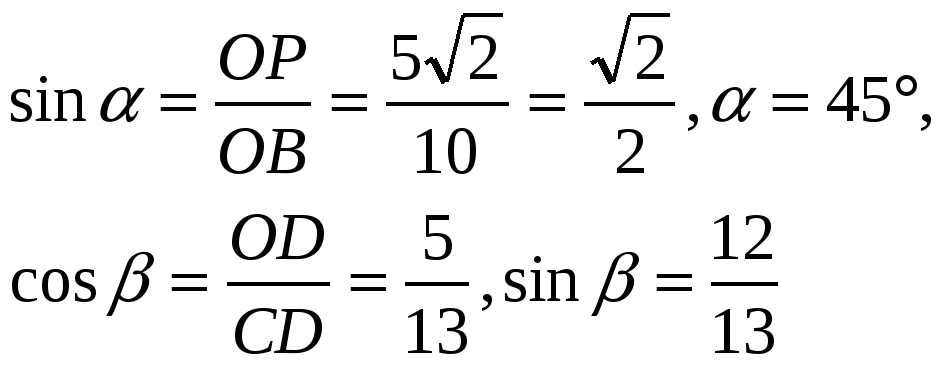
Применяя теорему синусов к треугольнику BMD получим,что , поэтому

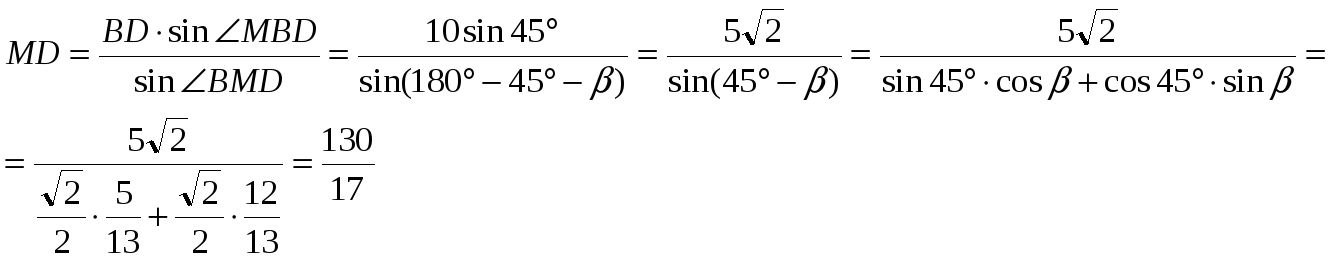
Следовательно, .

Случай 2.

Пусть теперь точка M лежит на продолжении стороны CD за точку D (Рис. 4 б)). Тогда по теореме о внешнем угле треугольника .

Делее, рассуждая аналогично, получим, что

.

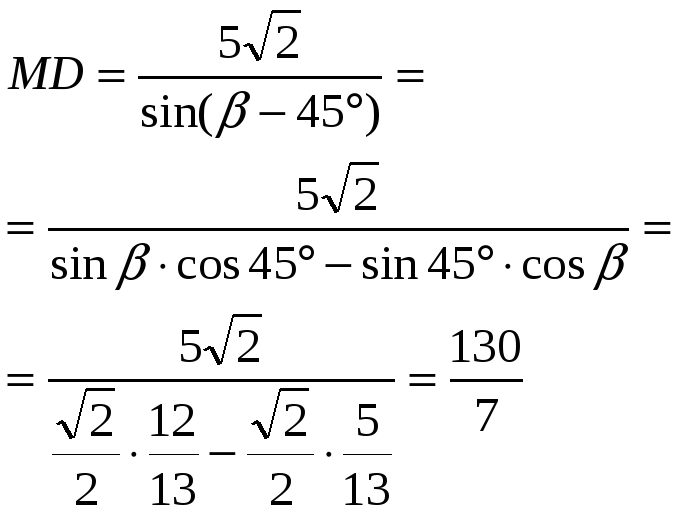Следовательно, .

Решение методом координат:

I случай (М лежит между С и D)

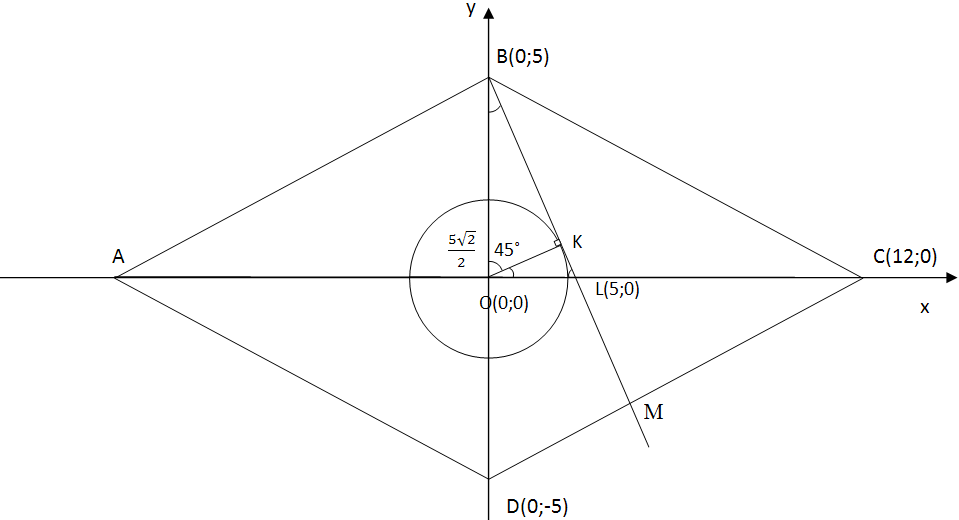
1. (по теореме Пифагора)

(KO – радиус, проведённый в точку касания прямой BL к окружности) ∆BOK – прямоугольный равнобедренный треугольник

, а так как ∆BOL – прямоугольный с острым углом в 45˚, то является ещё и равнобедренным () BO = OL = 5 (BO – половина диагонали BD, равной 10)

1. Введём прямоугольную систему координат с центром в точке О, тогда В(0; 5), L(5; 0), D(0; -5), С(12; 0), О(0; 0)

2. ВL – прямая ее можно задать уравнением вида y = kx + b, тогда

В(0; 5) b = 5

L(5; 0) 5k + 5 = 0; 5k = –5; k = –1

y = 5 – x – уравнение прямой BL

1. DC – прямая ее можно задать уравнением y = x + b, тогда

D (0; -5) b = –5,

С (12; 0) 12k – 5 = 0; 12k = 5; k =

y = х – 5 – уравнение прямой DC

1. Найдем координаты точки пересечения прямых BL и DC – точки М

5 – х = х – 5

1х +х = 10

x =

при х = y = 5 – х = 5 –=–= –= – 2

М (7; –2)

II случай (M лежит на продолжении CD)

1. Введём прямоугольную систему координат в точке О, тогда В(-5;0), L(0;5), D(5;0),

С(-12;0)

1. ВL – прямая её можно задать уравнением y = kx + b

L(0;5) b = 5

B(-5;0) –5k + 5 = 0

k = 1, y = х + 5 – уравнение прямой BL

1. CD – прямая её можно задать уравнением y = kx + b

С(0;-12) b = –12

D(5;0) 5k – 12 = 0; 5k = 12; k =2,4

y = 2,4х – 12 – уравнение прямой CD

1. Найдём координаты точки пересечения BL и CD – точки М

x + 5 = 2,4х – 12; 1,4х = 17; x = = 12; при х = 12; у = 12 + 5 = 17

М(12; 17)

Ответ: или .

Другие задачи по данным темам можно найти в Приложении 3, стр. II

Существует огромное количество конкурсных задач по планиметрии на различные комбинации фигур. В требованиях к этому заданию указано «Умение выполнять действия с геометрическими фигурами, координатами и векторами». В задаче С4 рассматривается конфигурация из двух геометрических фигур на плоскости. Для решения данной задачи нужно хорошо знать теоремы и формулы геометрии. В заданиях С4 предлагаются рисунки с типичными ситуациями расположения объектов: различных сочетаний треугольников, четырехугольников, окружностей. Для решения этих задач необходимо научиться искать стороны, отрезки, углы и площади геометрических фигур до автоматизма. Каждая новая комбинация фигур и данных в условии приносит свои подходы к решению, до которого бывает сложно догадаться. Даже если помнить все теоремы наизусть. Приходится набивать руку на решении большого количества задач. Необходимо научиться умению видеть применимость теорем для каждой конкретной задачи. Как правило, ученики помнят теорему, но часто не могут выявить ее в конкретной ситуации.

Рекомендации при решении задач по геометрии:

- внимательно прочитать условие задачи,

- построить чертеж, соответствующий условию (по возможности, наиболее наглядный),

- дать характеристику фигуре, вспомнить определение, свойства, признаки,

- определить зависимости между элементами,

- рассуждать от вопроса задачи, постепенно используя данные условия.

Таким образом, в результате самостоятельного изучения темы «Метод координат» проведено самостоятельное исследование решения геометрических задач части C ЕГЭ методом координат, позволившее:

• Показать решения разных типов экзаменационных геометрических задач части C методом координат;

• Доказать, что решение геометрических задач части C ЕГЭ методом координат является наиболее эффективным и простым способом, чем решение этих же задач традиционным способом;

• Выработать алгоритм решения задач типа C4.

Алгоритм решения задач типа C4

1. Введи прямоугольную систему координат, предварительно выбрав точку, которая будет являться ее центром.

2. Задай уравнения прямых по двум точкам.

3. Найди точку пересечения двух прямых.

4. Найди длину отрезка по двум известным точкам, одна из которых является точкой пересечения двух заданных уравнениями прямых.

5. Если нужно найти не длину отрезка, а, например, площадь фигуры, то, пользуясь основными формулами метода координат, найди недостающие элементы и вычисли то, что требуется в условии задачи.