Импликация и эквиваленция

Презентация для сопровождения объяснения темы "Логические операции: импликация и эквиаленция". Содержит определения, примеры и задания.

ИМПЛИКАЦИЯ

• это логическая операция, выражаемая связками " если...то… ", " из...следует… ", ".. .влечет. .. ".

) " width="640"

импликация (лат. implico –

тесно связаны) или

логическое следование обозначается знаком → (или = )

Пример:

А - " данный четырехугольник - квадрат"

В - "около данного четырехугольника можно описать окружность".

А → В = ?

Пример:

А - " данный четырехугольник - квадрат"

В - "около данного четырехугольника можно описать окружность".

А → В = "если данный четырехугольник квадрат, то около него можно описать окружность".

В обычной речи связка "если...то" описывает причинно-следственную связь между высказываниями. Но в логических операциях смысл высказываний не учитывается . Рассматривается только их истинность и ложность . Поэтому не надо смущаться "бессмысленностью" импликаций, образованных высказываниями, совершенно не связанными по содержанию. Например, такими: "если президент США - демократ, то в Африке водятся жирафы"

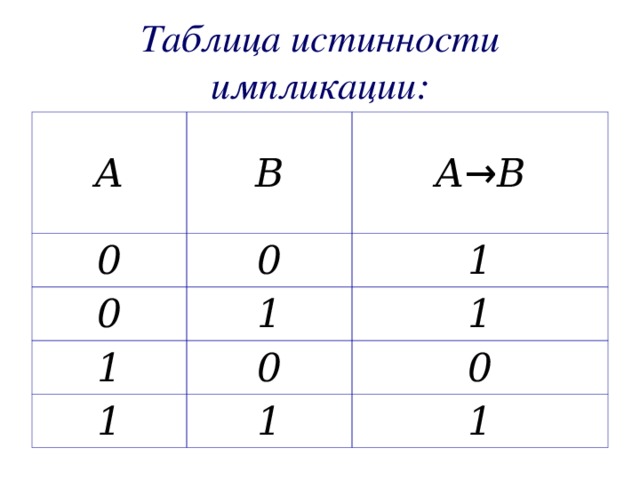
Таблица истинности импликации:

А

В

0

А → В

0

0

1

1

1

1

0

1

1

0

1

ЭКВИВАЛЕНЦИЯ

• это логическая операция, выражаемая связками

"тогда и только тогда", "необходимо и достаточно", "равносильно".

эквиваленция или логическое равенство обозначается знаком ↔ (может также обозначаться знаками ~ или ≡ ).

Высказывание А↔В истинно тогда и только тогда, когда значения А и В совпадают .

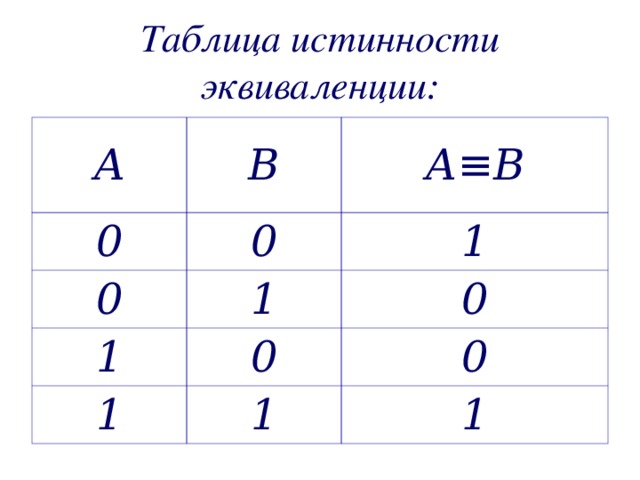
Таблица истинности эквиваленции:

А

В

0

А ≡ В

0

0

1

1

1

0

0

1

1

0

1

Задания: 1. Выделите в сложных суждениях простые и обозначьте их буквами. Представьте эти сложные суждения в виде формул:     а) Число делится на 6 тогда и только тогда, когда оно делится на 2 и на 3.

Число делится на 6 тогда и только тогда, когда оно делится на 2 и на 3. А=«Число делится на 6» В=«Число делится на 2» С=«Число делится на 3»

Ответ : А≡(В·С)

    б).  Если завтра не будет дождя, то мы пойдем купаться на речку или пойдем собирать грибы в лес.

Ответ: Ā→(В+С)

Какой логической формуле соответствует следующее составное высказывание: "Для того чтобы параллелограмм был квадратом, необходимо и достаточно, чтобы он был ромбом и имел прямой угол или был прямоугольником и имел равные смежные стороны". a) (Y · X) + (K · L); b) (Y + X) + (K + L); c) (Y · X) · (K · L).

Алгоритм построения таблицы истинности: - подсчитать количество переменных n в логическом выражении; - определить число строк в таблице, которое равно m = 2n; - подсчитать количество операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество операций; - ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов; - заполнить столбцы входных переменных наборами значений; - провести заполнение таблицы значениями (0 и 1) истинности по столбцам, выполняя логические операции.

Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания ("не"), затем конъюнкция ("и"), после конъюнкции - дизъюнкция ("или") и в последнюю очередь импликация и эквиваленция .

Порядок выполнения логических операций: 1. отрицания ("не"), 2. конъюнкция ("и"), 3. дизъюнкция ("или"), 4. импликация, 5. эквиваленция .

Например, построим таблицу истинности для логического выражения Y= A→B &¬A

Y= A→B &¬A

А

В

0

¬A

0

0

B &¬A

1

1

1

1

0

1

0

A→B &¬A

1

1

0

1

1

0

0

0

0

0

Например, построим таблицу истинности для логического выражения Y=¬(A→(B→C))~(A&B&¬C)

A

B

0

0

0

C

0

B → C

0

0

1

1

0

1

A → (B → C)

1

0

1

1

1

¬(A → (B → C))

0

1

1

0

¬C

0

1

1

1

0

1

1

A&B

0

0

1

A&B&¬C

1

1

0

0

1

1

0

1

1

1

0

0

1

0

0

Y

0

0

1

1

1

0

0

0

0

1

1

0

0

0

1

1

0

1

1

0

0

1

0

1

0

0

1

0

1

0

1

1

1

1

0

1

Построить таблицы истинности для логических выражений: 1).  A+(B+¬B→¬C) 2). A&(B&¬B→C) 3).  A+(B+¬B)&A+(B→C)