Игры с числами
1. Волшебная красота магических квадратов.
Красивы не только они сами, но и приемы их составления. Занимателен такой прием составления магического квадрата 7 × 7 из последовательности натуральных чисел. В отчеркнутую часть квадрата 7 × 7 вписана «диагонально» последовательность нечетных чисел (1, 3, …, 49). Из оставшихся «уголков» скомпонована симметричная фигура, в клетки которой также «диагонально» вписана последовательность четных чисел (2, 4, …, 48). Теперь завершающим этапом конструирования магического квадрата является задача: разъединить вторую фигуру на «уголки» и приставить их к первой фигуре так, чтобы образовался магический квадрат 7 × 7.
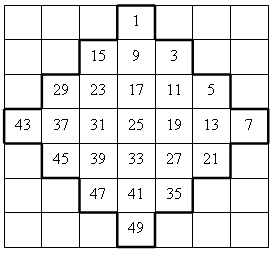
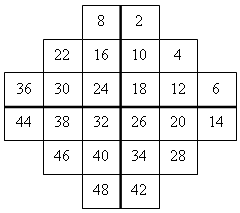
2. Расставьте цифры, помещенные в квадратиках, так, чтобы суммы чисел по любой горизонтали, вертикали и диагонали (из угла в угол большого квадрата) были равны а) 27; б) 6; в) 9; г) 18.
а) 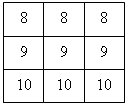 б)
б) 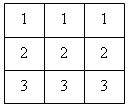
в)  г)
г) 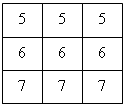
3. Переместите цифры, помещенные в квадратиках, так, чтобы суммы чисел по любой горизонтали, вертикали и диагонали большого квадрата были одинаковы, но притом на каждой из названных прямых не встречались две одинаковые цифры.
| 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 2 | 2 |
| 3 | 3 | 3 | 3 | 3 |
| 4 | 4 | 4 | 4 | 4 |
| 5 | 5 | 5 | 5 | 5 |
4. Числа 1, 2, 3, 4, 5, 6, 7, 8 и 9 требуется разместить в 9 клетках квадрата так, чтобы суммы чисел по любой его горизонтали, вертикали и диагонали были одинаковы и составляли каждый раз число 15.
|
|
|
|
|
|
|
|
|
|
|
|
5. Числа 2, 3, 4, 5, 6, 7, 8, 9 и 10 требуется разместить в 9 клетках квадрата и притом так, чтобы суммы чисел по любой его горизонтали, вертикали и диагонали были одинаковы и составляли число 18.
|
|
|
|
|
|
|
|
|
|
|
|
6. Числа 0, 1, 2, 3, 4, 5, 6, 7 и 8 требуется разместить в 9 клетках квадрата и притом так, чтобы суммы чисел по любой его горизонтали, вертикали и диагонали были одинаковы и составляли число 12.
| | | |
| | | |
| | | |
7. В квадрате расставьте цифры (по одной в каждой клетке) 0, 1, …, 24 включительно так, чтобы суммы чисел по любой горизонтали, вертикали и диагонали были одинаковы и каждая из этих сумм равнялась 60.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. Расположите все цифры, помещенные в данной фигуре, по клеткам закрашенного квадрата так, чтобы суммы чисел по любой горизонтали, вертикали и диагонали были одинаковы и каждая из них была равна 15 (использовать метод террас).
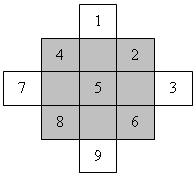
9. Расположите все цифры, помещенные в данной фигуре, по клеткам закрашенного квадрата так, чтобы суммы чисел по любой горизонтали, вертикали и диагонали были одинаковы и каждая из них была равна 65 (использовать метод террас).
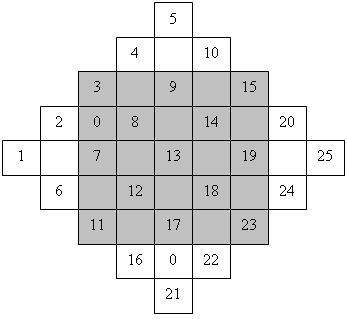
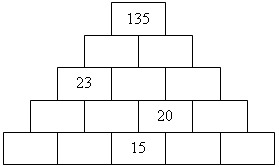
10. Числовые пирамиды.
Известное число – это сумма чисел в двух клетках под ним. Следуя этому правилу и учитывая, что на первом этаже кроме цифры 15 находятся цифры 3, 11, 2, 5, заполните пустые клетки.
11. Каждый кирпичик этой числовой пирамиды является суммой кирпичиков, расположенных сразу под ним. Заполните все клетки пирамиды так, чтобы прийти к числу 217 на ее вершине.

12. Известное число – это разность чисел в двух клеточках под ним. Причем в левой клеточке находится уменьшаемое, в правой – вычитаемое. Следуя этому правилу, заполните пустые клеточки.

13. Известное число – это произведение чисел в двух клеточках под ним. Следуя этому правилу, заполните пустые клеточки.
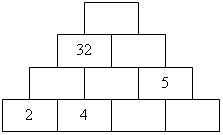
14. Пройдите от вершины пирамиды к ее основанию, переходя из каждой клетки в одну из расположенных под ней, и наберите по дороге заданную сумму (35, 45, 55).
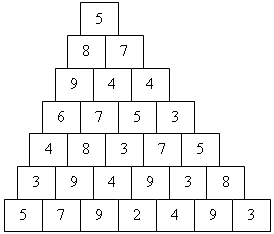
15. Пройдите от вершины пирамиды к ее основанию, переходя из каждой клетки в одну из расположенных под ней, и наберите по дороге заданную сумму (40, 50, 60).

16. Девять кружков образуют вершины 4 малых и больших равнобедренных треугольников. Требуется вписать в эти кружки числа от 1 до 9 так, чтобы суммы чисел, стоящих в вершинах каждого из равнобедренных треугольников, были равны.

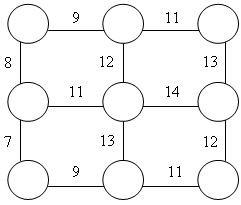
17. Впишите в кружочки цифры от 1 до 9 таким образом, чтобы сумма чисел в любых двух соседних кружочках равнялась числу, написанному между этими кружочками.
18. Разделите изображенную на рисунке двухрядную полоску на четыре конгруэнтные части так, чтобы сумма чисел в клетках была равна 34.
| 1 | 9 | 16 | 7 | 12 | 5 | 4 | 3 |
| 8 | 15 | 10 | 2 | 13 | 6 | 11 | 14 |
19. В квадрате записаны цифры. Найдите такой путь от цифры 1 в верхнем левом углу до цифры 9 в нижнем правом углу, чтобы сумма всех чисел была равна 75. Двигаться можно только вправо и вниз. Затем, соблюдая эти же правила, наберите в сумме 100. Двигаясь в трех направлениях (вправо, влево, вниз), наберите в сумме 120, 180.
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
| 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 |
| 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
20. Числовой треугольник.
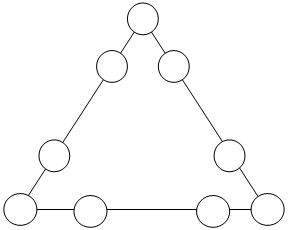
а) Расставьте числа от 1 до 9 в треугольнике так, чтобы суммы чисел в четырех кружках для каждой стороны треугольника были равны 17.
б) Расставьте числа от 116 до 916 в треугольнике так, чтобы суммы чисел в четырех кружках для каждой стороны треугольника были равны 20.
21. Магическая звезда.
а) Расставьте числа от 1 до 12 в шестиконечной числовой звезде так, чтобы суммы чисел в четырех кружках для каждой стороны звезды были равны.
б) Расставьте числа от 1 до 12 в шестиконечной числовой звезде так, чтобы суммы чисел в четырех кружках для каждой стороны звезды были равны 26, сумма чисел на концах искомой звезды равна 26, а сумма же всех чисел звезды равна 78.
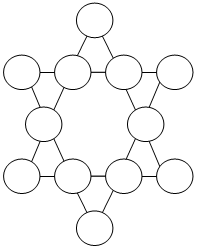
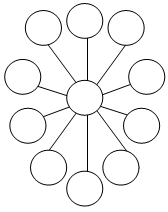
22. Числовое кольцо.
Цифры от 1 до 9 разместите в кольце так, чтобы одна цифра была в центре кольца, прочие – у концов каждого диаметра и чтобы сумма трех чисел каждого ряда составляла 15.
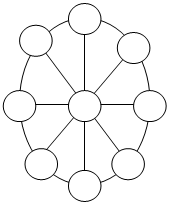
23. Восьмиконечная звезда.
Числа от 1 до 16 расставьте в точках пересечения линий фигуры так, чтобы сумма чисел на стороне каждого квадрата была 34, и сумма их на вершинах каждого квадрата также составляла 34.
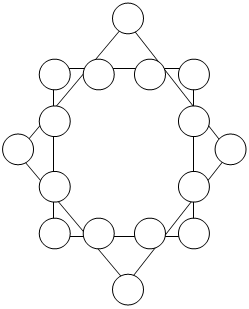
24. Куб.
Расставьте цифры 1, 2, 3, 4, 5, 6, 7, 8 в вершинах куба так, чтобы суммы цифр, стоящих в каждой грани, были равны.
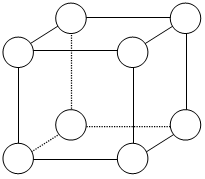
25. Расстановка цифр.
Цифры от 1 до 8 расставьте в восьми кружках фигуры так, чтобы никакие два последовательных числа не стояли в кружках, соединенных друг с другом «напрямик». Например, если в самом верхнем кружке стоит цифра 5, то ни в одном из трех кружков (B, C, D) следующего ряда уже нельзя вписать цифру 4 или 6, потому что каждый из этих кружков соединяется с верхней линией. Существует единственное решение задачи (решения, переходящие друг в друга при поворотах и отражениях, различными не считаются), но найти его простым подбором, без анализа, довольно трудно.

26. Начертите квадрат и разделите его на 16 клеток (4 × 4). Впишите в клетки квадрата числа от 1 до 16 так, чтобы сумма чисел по горизонтали, вертикали и по диагоналям равнялась 34.
27. Арифметическая спираль.
Расставьте знаки в пустых клетках так, чтобы получить в результате 5.
| 7 |
| 4 |
| 3 |
|
| 9 |
| 5 |
|
| 5 |
| 1 |
| 6 |
|
|
|
|
|
|
28. Разместите на кружках фигуры числа от 1 до 12 так, чтобы сумма чисел в кружках каждого заштрихованного квадрата равнялась 30.

29. Числа 1, 2, 3, 4, 5, 6, 10, 12, 15, 20 и 30 разместите так, чтобы произведение любых чисел, лежащих в трех кружках на прямой линии, было равно 60.
30. Одинаковые суммы.
Найдите по два квадрата (2 × 2), в каждом из которых суммы чисел равны 18, 19, 2 и 25, и по два квадрата (3 × 3), в каждом из которых суммы чисел равны 41 и 45.
| 2 | 1 | 9 | 5 | 4 | 6 |
| 3 | 4 | 8 | 3 | 7 | 8 |
| 6 | 5 | 6 | 2 | 1 | 5 |
| 7 | 3 | 4 | 3 | 2 | 7 |
| 8 | 6 | 7 | 8 | 4 | 6 |
| 9 | 4 | 1 | 9 | 3 | 8 |
31. Поиск магических квадратов.
В таблице много разных чисел, но среди них есть числа, образующие два магических квадрата: один квадрат (4 × 4 клеток), в котором сумма чисел по горизонтали, вертикали и диагонали равна 34, другой (5 × 5 клеток), в котором сумма чисел равна 65. Требуется найти эти квадраты.
| 8 | 37 | 54 | 31 | 24 | 19 | 8 | 6 | 21 | 31 |
| 6 | 39 | 7 | 9 | 11 | 14 | 12 | 5 | 3 | 7 |
| 9 | 1 | 16 | 10 | 13 | 7 | 1 | 16 | 10 | 13 |
| 7 | 9 | 12 | 24 | 16 | 4 | 6 | 11 | 13 | 10 |
| 5 | 25 | 10 | 3 | 11 | 9 | 15 | 2 | 8 | 11 |
| 3 | 6 | 3 | 20 | 12 | 24 | 21 | 53 | 17 | 12 |
| 1 | 15 | 22 | 9 | 1 | 18 | 18 | 9 | 22 | 15 |
| 2 | 4 | 16 | 13 | 25 | 7 | 6 | 3 | 20 | 24 |
| 6 | 23 | 10 | 2 | 19 | 11 | 18 | 23 | 11 | 14 |
| 0 | 17 | 14 | 21 | 8 | 5 | 17 | 6 | 3 | 20 |
32. Магический треугольник.
Расставьте числа от 1 до 9 в треугольнике так, чтобы суммы чисел в четырех кружках для каждой стороны треугольника были равны а) 20 и 126, б) по внутренним треугольникам – 25 и 159, в) суммы чисел в пяти кружках равны 25.
33. Дано число 123456789101112131415 … 9899100. Вычеркните 100 цифр так, чтобы оставшееся число было наибольшим.
34. Постройте магический квадрат из одних простых чисел.
|
|
|
|
|
|
|
|
|
|
|
|
35. Из девяти цифр от 1 до 9 составьте три простых числа так, чтобы их сумма была минимальной. Каждую цифру разрешается использовать только один раз. Например, числа 941, 827 и 653 простые и удовлетворяют последнему требованию, но их сумма (2421) не минимальна.
36. Найдите составное число среди следующих чисел:
31, 331, 3331, 33331, 333331, 3333331, 33333331, 333333331.
37. Укажите четыре простых числа среди следующих шести чисел:
10 001; 14 159; 76 543; 77 377; 123 456 789;
909 090 909 090 909 090 909 090 909 090.
38. Существует такой случай умножения двух чисел: 48 × 159 = 7632. Он замечателен тем, что в нем участвуют по одному разу все девять значащих цифр. Найдите еще несколько таких примеров. Сколько их, если они существуют?
39. В свободные клетки впишите такие числа, чтобы по всем горизонталям, вертикалям и двум диагоналям в сумме получилось одно и то же число.
| 55 |
|
|
|
|
| 60 |
| 75 | 50 |
|
40. В свободные клетки впишите такие числа, чтобы по всем горизонталям, вертикалям в сумме получилось 60.
| 16 |
|
|
| 16 |
|
| 16 |
| 16 |
|
|
|
| 16 |
|
|
|
| 16 |
| 16 |
|
| 16 |
|
|
| 16 |
41. Найдите наименьшее натуральное число, которое оканчивается на 56, делится на 56 и имеет сумму цифр, равную 56.
42. Расставьте в кружочки цифры от 1 до 8 так, чтобы в горизонтальных рядах получились числа, являющиеся квадратами, а сумма чисел, расположенных в центрально-симметричных кружках, была одна и та же.
43. Магический треугольник.
Используя основные константы, составьте магический треугольник из чисел 1 – 6 и 13 – 15, уплотненный магический треугольник из чисел 7 – 12 так, чтобы сумма внешнего треугольника равнялась 23, для внутреннего треугольника – 27; используя дополнительные константы, получите суммы: 29, 18, 24, 30, 41, 23 и 40.
44. Размещенные в треугольничках рисунка десять четных чисел переставьте таким образом, чтобы суммы каждых четырех чисел в больших треугольниках (левом, правом, нижнем и центральном) были между собой одинаковы и равнялись 50.
45. Размещенные в треугольничках рисунка десять четных чисел переставьте с таким расчетом, чтобы суммы каждых четырех чисел в больших треугольниках (левом, правом, нижнем) были между собой одинаковы и равнялись 25.
46. Расставьте числа от 1 до 10 так, чтобы сумма трех чисел, расположенных на углах каждого треугольника звезды, составляла а) 14, б) 16.
47. Расставьте числа от 1 до 8 в кружки фигуры так, чтобы сумма чисел на каждой окружности была одной и той же.
48. Переставьте числа в кружках этой фигуры так, чтобы сумма чисел любой из сторон большого треугольника равнялась 11, а сумма чисел в каждом из малых треугольников была равна 10.
49. Расставьте числа от 1 до 12 так, чтобы по двум центральным, вертикальным и горизонтальным рядам, а также в четырех кругах, квадратах и треугольниках сумма цифр была равна 26.
50. Числа в две строки.
Первые 8 чисел можно расставить в две строки так, что сумма чисел в нижней строке будет равна сумме чисел в верхней строке, а суммы чисел в столбцах также равны между собой.
| 1 | 7 | 6 | 4 |
| 8 | 2 | 3 | 5 |
Можно ли подобным образом расставить:
1) первые 12 чисел?
2) первые 16 чисел?

 Получите свидетельство
Получите свидетельство Вход
Вход












 Игры с числами по информатике в рамках внеурочной деятельности (212.6 KB)
Игры с числами по информатике в рамках внеурочной деятельности (212.6 KB)
 0
0 608
608 5
5 Нравится
0
Нравится
0


