Евклид (Эвклид)

Евклид (Эвклид)

Годы жизни: примерно 325 год до н. э. – 265 год до н. э.

Сфера деятельности: Наука, Математика, Геометрия

Достижение: Стал автором Евклидовой Геометрии и учебника Элементы, который использовался вплоть до XIX века.

Биография Евклида

• Евклид родился в середине 3-го века до нашей эры и жил в Александрии, на территории Египта; пик его творческой деятельности пришелся на время правления Птолемея I (323-283 до н.э), а его имя Евклид означает «известный, славный». В некоторых источниках он также упоминается, как Евклид Александрийский.
• Вероятно, Евклид работал с командой математиков в Александрии, и он получил степень при помощи его математических работ. Некоторые историки считают, что работы Евклида, возможно, были результатом нескольких авторов, но большинство согласны с тем, что один человек – Евклид – был главным автором.
• Вполне вероятно, что Евклид учился в Академии Платона в Афинах, и большая часть его знаний пришла оттуда. Именно там он впервые познакомился с математикой, а именно с одной ее частью – геометрией.
• О личной жизни математика неизвестно – почти все время он посвящал науке.

Постулаты Евклида

• Его главная книга «Элементы» (первоначально написанная на древнегреческом языке) стала базовой работой важных математических учений. Она разделена на 13 отдельных книг.
• Книги от первой до шестой посвящены геометрии плоскости.
• Книги семь-девять имеют дело с теорией чисел
• Книга восьмая о геометрической прогрессии
• Книга десятая посвящена иррациональным числам
• Книги одиннадцать-тринадцать представляют собой трехмерную геометрию (стереометрию).
• Гений Евклида состоял в том, чтобы взять в оборот множество разнообразных элементов математических идей и объединить их в один логический, последовательный формат.

Ватиканский манускрипт

Ватиканский манускрипт (XI, Предложения, 31—33) Классический труд Евклида, написанный в 3 веке до н.э., посвященный , прежде всего, аксиоматическому построению геометрии, а также включавший основы теории чисел, общей теории отношений величин и методов нахождения площадей и объемов с элементами теории пределов. Этот трактат служил учебником геометрии более 1000 лет и современные учебники во многом опираются на заложенные в нем идеи. В свою очередь, Евклид использовал труды Гиппократа, Евдокса, Архита и Теэтета.

Алгоритм Евклид

• Используя лемму Евклида, эта теорема утверждает, что каждое целое число больше единицы либо само по себе простое число, либо произведение простых чисел и что существует определенный порядок простых чисел.
• «Если два числа, умножая одно на другое, составляют некоторое число, и любое число, которое делится на их произведение, также будет делиться на каждое из исходных чисел».
• Евклидов алгоритм — эффективный метод вычисления наибольшего общего делителя (НОД) двух чисел, наибольшего числа, которое делит их оба, не оставляя остатка.

Геометрия Евклида

Евклидова геометрия — это геометрическая теория, основанная на системе аксиом, которая была впервые изложена в третьем веке до нашей эры великим древнегреческим математиком Евклидом в грандиозном научном труде «Начала».

• В «Началах» Евклид представил следующую аксиоматику:
• От всякой точки до всякой точки можно провести прямую.
• Ограниченную прямую можно непрерывно продолжать по прямой.
• Из всякого центра всяким раствором может быть описан круг.
• Все прямые углы равны между собой.
• Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых.

Система аксиом Евклида.

В современной трактовке система аксиом Евклида может быть разделена на пять групп:

• Аксиомы сочетания. Во-первых, через каждые две точки можно провести прямую и притом только одну. Во-вторых, на каждой прямой лежат по крайней мере две точки. При этом существуют хотя бы три точки, которые не лежат на одной прямой. В-третьих, через каждые три точки, не лежащие на одной прямой, можно провести плоскость и притом только одну. В-четвертых, на каждой плоскости есть по крайней мере три точки, а также существуют хотя бы четыре точки, не лежащие в одной плоскости. В-пятых, если две точки данной прямой лежат на данной плоскости, значит и сама прямая лежит на этой плоскости. В-шестых, если две плоскости имеют общую точку, то, следовательно они имеют и общую прямую.
• Аксиомы порядка. Во-первых, если точка В лежит между А и С, то все три лежат на одной прямой. Во-вторых, для каждых точек А, В существует такая точка С, что В лежит между А и С. В-третьих, из трёх точек прямой только одна лежит между двумя другими. В-четвертых, если прямая пересекает одну сторону треугольника, значит она пересекает при этом и другую его сторону или проходит через вершину (отрезок AB определяется как множество точек, лежащих между А и В; аналогично определяются стороны треугольника).
• Аксиомы движения. Во-первых, движение ставит в соответствие точкам точки, прямым прямые, плоскостям плоскости, сохраняя принадлежность точек прямым и плоскостям. Во-вторых, два последовательных движения вновь дают движение, и для всякого движения есть обратное. В-третьих, если даны точки А, A’ и полуплоскости A, A‘, ограниченные продолженными полупрямыми а, а’, которые исходят из точек А, A’, то существует единственное движение, переводящее А, а, A в A’, a’, A’ (полупрямая и полуплоскость легко определяются на основе понятий сочетания и порядка).
• Аксиомы непрерывности. Во-первых, как гласит аксиома Архимеда, всякий отрезок можно перекрыть любым отрезком, откладывая на первом его достаточное количество раз (откладывание отрезка осуществляется движением). Во-вторых, согласно аксиоме Кантора: если дана последовательность отрезков, вложенных один в другой, то все они имеют хотя бы одну общую точку.
• Аксиома параллельности Евклида: через точку А вне прямой а в плоскости, проходящей через А и а, можно провести лишь одну прямую, не пересекающую а

АКСИОМЫ ЕВКЛИДА

• 1. Равные одному и тому же равны и между собой. 2. И если к равным прибавляются равные, то и целые будут равны. 3. И если от равных отнимаются равные, то остатки будут равны. 4. И если к неравным прибавляются равные, то и целые не будут равны. 5. И удвоенные одного и того же равны между собой. 6. И половины одного и того же равны между собой. 7. И совмещающиеся друг с другом равны между собой. 8. И целое больше части. 9. И две прямые не содержат пространства.

Лобачевский Николай Иванович (1792-1856)

Русский математик, создатель неевклидовой геометрии Заменив V постулат Евклида на аксиому, Лобачевский Н.И. пришел к выводу, что можно построить другую геометрию, отличную от евклидовой.

• Геометрия Лобачевского (гиперболическая геометрия) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского. Евклидова аксиома о параллельных гласит: Через точку, не лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её. В геометрии Лобачевского, вместо неё принимается следующая аксиома: Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её. Широко распространено заблуждение, что в геометрии Лобачевского параллельные прямые пересекаются. Геометрия Лобачевского имеет обширные применения как в математике, так и в физике. Историческое её значение состоит в том, что её построением Лобачевский показал возможность геометрии, отличной от евклидовой, что знаменовало новую эпоху в развитии геометрии, математики и науки вообще.

• Евклидова геометрия — геометрическая теория, основанная на аксиомах, впервые изложенной в «Началах» Евклида (III век до н. э.). «Начала состоят из 15 книг. В I книге изучаются свойства треугольников и параллелограммов; эту книгу венчает знаменитая теорема Пифагора для прямоугольных треугольников. Книга II, восходящая к пифагорейцам, посвящена так называемой «геометрической алгебре». В III и IV книгах излагается геометрия окружностей, а также вписанных и описанных многоугольников; при работе над этими книгами Евклид мог воспользоваться сочинениями Гиппократа Хиосского. В V книге вводится общая теория пропорций, построенная Евдоксом Книдским, а в VI книге она прилагается к теории подобных фигур. VII—IX книги посвящены теории чисел и восходят к пифагорейцам; автором VIII книги, возможно, был Архит Тарентский. Остальные книги связаны с алгеброй. Евклидову геометрию называют элементарной геометрией.

«Чем отличается геометрия Лобачевского от геометрии Евклида?»

• Евклидова аксиома о параллельных прямых: через точку, не лежащую на данной прямой, проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающие её.
• Аксиома Лобачевского о параллельных прямых: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
• ВЫВОД: Геометрия Лобачевского отличается от евклидовой лишь в одной аксиоме — пятой. Но главное различие кроется в понимании самой природы пространства.

• Фридрих Бернхард Риман (1826-1866) Немецкий математик, создатель новой геометрии, которая обобщает как геометрию Евклида, так и геометрию Лобачевского.

• Давид Гильберт (1862-1942) Немецкий математик, написал «Основания геометрии», в которых рассматриваются проблемы непротиворечивости, полноты и независимости систем аксиом, определяющих ту или иную геометрию.

Феликс Христиан Клейн (1849—1925)

Немецкий математик и педагог. Автор Эрлангенской программы. Первым строго доказал непротиворечивость геометрии Лобачевского. Внёс значительный вклад в общую алгебру (особенно в теорию групп и теорию непрерывных групп), теорию эллиптических и автоморфных функций. Член Берлинской академии наук (1913), иностранный член-корреспондент Петербургской академии наук (1895). Первый председатель Международной комиссии по математическому образованию

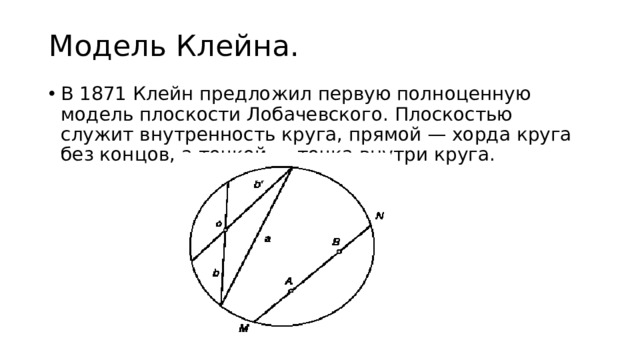
Модель Клейна.

• В 1871 Клейн предложил первую полноценную модель плоскости Лобачевского. Плоскостью служит внутренность круга, прямой — хорда круга без концов, а точкой — точка внутри круга.

Помимо геометрии, Евклид исследовал и другие отрасли математики. Однако стоит признать, что вклад Евклида в науку огромен – без него, наверно, математика не смогла бы настолько продвинуться перед учеными. Его имя неразрывно связано с геометрией, изучением пространства.