Екі (үш) жүйелі теңдеуді Крамер формуласы бойынша шешу.
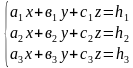 – үшінші ретті сызықтық теңдеу жүйесі.
– үшінші ретті сызықтық теңдеу жүйесі.
Теңдеулер жүйесінің үйлесімді болуының жеткілікті шарты
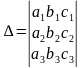
анықтауышының нөлге тең болмауы. Бұл жағдайда жүйенің шешуін төмендегі формула арқылы табады:
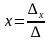
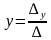
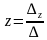
Мысал. 1) Сызықтық теңдеулер жүйесiн шешу.
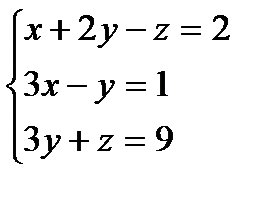
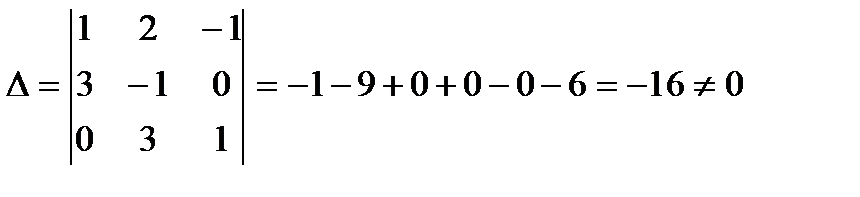
Шешуi:
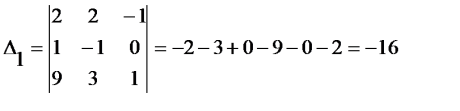
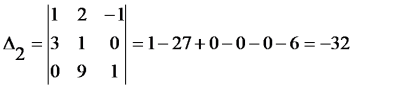
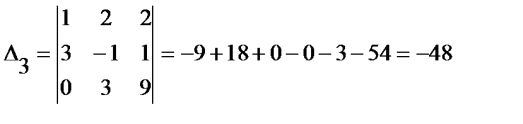
Демек берiлген жүйе шешуi:
![]()
![]()
![]()
Теңдеулер жүйесiн шешiңдер:
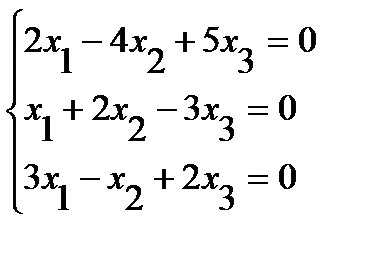
Шешуi. Жүйенiң анықтауышын табайық:
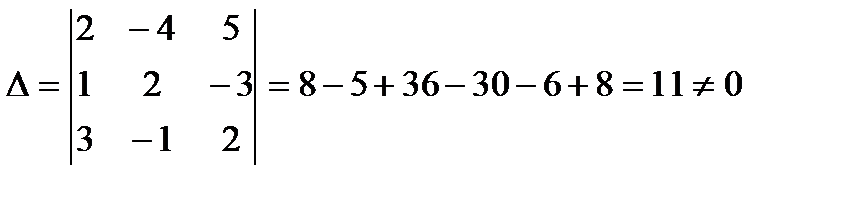
Демек берiлген теңдеулер жүйесiнiң тек бiр шешуi болады. Ол нөлдiк шешу: x1=x2=x3=0
Кері матрица.
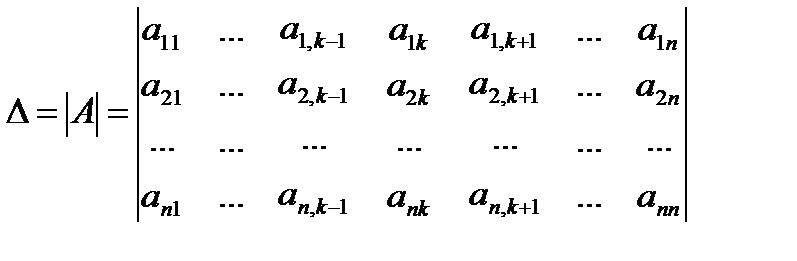 (1)
(1)
Берілген (1) жүйені кері матрица әдісімен шешу үшін осы жүйенің төмендегі матрицаларын қарастырайық:
A = 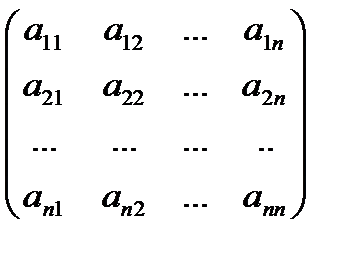 ; Х =
; Х = ![]() ; B =
; B = ![]() ;
;
Мұндағы 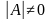 болсын, Х – белгісіз n
болсын, Х – белгісіз n 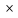 1 өлшемді матрица.
1 өлшемді матрица.
Матрицаларға қолданылатын амалдарға сүйене отырып, А мен Х матрицаларының көбейтіндісі (1) жүйенің сол жағындағы өрнектен анықталған матрицаға тең деп аламыз. Алдымен А мен Х матрицаларының көбейтіндісін анықтайық:
А*Х = 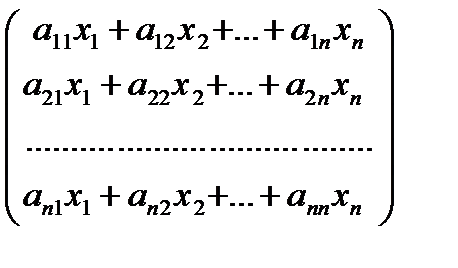
А*Х пен В матрицаларының теңдігінен мына теңдеуді аламыз:
А*Х = В; (4)
Мұндағы, Х – белгісіз n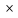 1 матрица және
1 матрица және 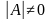 (4) теңдеу (1) жүйенің матрица түріндегі теңдеуі деп аталады.
(4) теңдеу (1) жүйенің матрица түріндегі теңдеуі деп аталады.
Берілген жүйенің матрицасы ерекше емес матрица, сондықтан оның кері матрицасы бар.
Енді (4) теңдеудің шешімін табу үшін осы теңдеуді солдан оңға қарай А матрицасының кері матрицасына көбейтейік:
А-1*А*Х=А-1*В
Мұндағы, А-1*А=Е және Е*Х=Х. Олай болса
Х=А-1*В (5)
болады, мұндағы А-1*В – көбейтіндісі бар.
Топпен жұмыс:
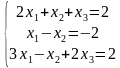
Жеке тапсырмалар:
1)

 Получите свидетельство
Получите свидетельство Вход
Вход












 Екі (үш) жүйелі теңдеуді Крамер формуласы бойынша шешу. (181.73 KB)
Екі (үш) жүйелі теңдеуді Крамер формуласы бойынша шешу. (181.73 KB)
 0
0 513
513 0
0 Нравится
0
Нравится
0


