1. Тип 1 № 13560 ![]()
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длине этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | П8 | |
| П1 | 15 | 20 | 18 | |||||
| П2 | 15 | 25 | ||||||
| П3 | 25 | 24 | 22 | |||||
| П4 | 20 | 12 | ||||||
| П5 | 13 | 16 | 17 | |||||
| П6 | 24 | 13 | 15 | |||||
| П7 | 12 | 16 | ||||||
| П8 | 18 | 22 | 17 | 15 |
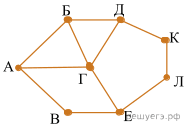
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину дороги из пункта Е в пункт Л. В ответе запишите целое число.
2. Тип 2 № 29109 ![]()
Логическая функция F задаётся выражением ((z → w) ∨ (y ≡ w)) ∧ ((x ∨ z) ≡ y). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| ? | ? | ? | ? | F |
|---|---|---|---|---|
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | ||
| 0 | 1 | 1 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
3. Тип 3 № 37494 ![]()
В файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц.
3.xlsx
Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой декады июня 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок, шт. занесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Заголовок таблицы имеет следующий вид.
| ID операции | Дата | ID магазина | Артикул | Тип операции | Количество упаковок,шт. | Цена,руб./шт. |
Таблица «Товар» содержит информацию об основных характеристиках каждого товара. Заголовок таблицы имеет следующий вид.
| Артикул | Отдел | Наименование | Ед. изм. | Количествов упаковке | Поставщик |
Таблица «Магазин» содержит информацию о местонахождении магазинов. Заголовок таблицы имеет следующий вид.
| ID магазина | Район | Адрес |
На рисунке приведена схема указанной базы данных.
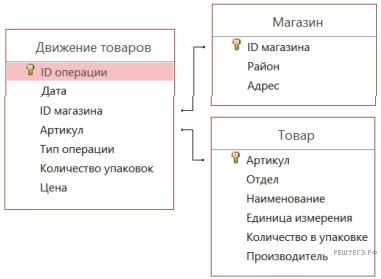
Используя информацию из приведённой базы данных, определите, сколько рублей выручили магазины Заречного района от продажи соды пищевой за период с 1 по 10 июня включительно.
В ответе запишите только число.
4. Тип 4 № 16434 ![]()
По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, Н, Р, Т. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Г — 110, И — 01, Т — 10. Какое наименьшее количество двоичных знаков потребуется для кодирования слова БАРАБАН?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
5. Тип 5 № 16033 ![]()
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу:
а) если N чётное, в конец числа (справа) дописывается сначала ноль, а затем единица.
б) если N нечётное, справа дописывается сначала единица, а затем ноль.
Например, двоичная запись 100 числа 4 будет преобразована в 10001, а двоичная запись 111 числа 7 будет преобразована в 11110.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа R — результата работы данного алгоритма.
Укажите минимальное число R, которое больше 102 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.
6. Тип 6 № 58246 ![]()
Исполнитель Цапля действует на плоскости с декартовой системой координат. В начальный момент Цапля находится в начале координат, её клюв направлен вдоль положительного направления оси ординат, клюв опущен. При опущенном клюве Цапля оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует три команды: Вперёд n (где n — целое число), вызывающая передвижение Цапли на n единиц в том направлении, куда указывает её клюв; Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке; Дуга r, a, b, α (где r, a, b, α — целые числа), вызывающая передвижение Цапли из текущей точки с координатами (x, y) по дуге окружности с центром в точке с координатами ![]() и радиусом r, градусная мера дуги равна α, движение по дуге идёт по часовой стрелке.
и радиусом r, градусная мера дуги равна α, движение по дуге идёт по часовой стрелке.
Запись Повтори k [Команда 1 Команда 2 ... Команда S] означает, что последовательность из S команд повторится k раз.
Цапле был дан для исполнения следующий алгоритм:
Направо 180 Вперёд 2 Направо 90 Вперёд 40 Направо 90 Вперёд 2 Повтори 4 [Дуга 5, 5, 0, 180].
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
7. Тип 7 № 35896 ![]()
В информационной системе хранятся изображения размером 1024 × 768 пикселей. Методы сжатия изображений не используются. Каждое изображение дополняется служебной информацией, которая занимает 640 Кбайт. Для хранения 2048 изображений потребовалось 2 Гбайт. Сколько цветов использовано в палитре каждого изображения?
8. Тип 8 № 7986 ![]()
Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв З, И, М, А? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
9. Тип 9 № 59833 ![]()
Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия:
— в строке есть только два равных числа, остальные 4 различны;
— среднее арифметическое повторяющихся чисел меньше, чем среднее арифметическое остальных чисел строки.
В ответе запишите только число.
Задание 9
10. Тип 10 № 36023 ![]()
Определите, сколько раз в тексте произведения А. С. Грибоедова «Горе от ума», не считая сносок, встречается слово «батюшка» или «Батюшка». Другие формы слова «батюшка», такие как «батюшке», «батюшки» и т. д., учитывать не следует. В ответе укажите только число.
Задание 10
11. Тип 11 № 18589 ![]()
Каждый сотрудник предприятия получает электронный пропуск, на котором записаны личный код сотрудника, код подразделения и некоторая дополнительная информация. Личный код состоит из 13 символов, каждый из которых может быть одной из 16 допустимых заглавных букв или одной из 10 цифр. Для записи личного кода используют посимвольное кодирование, все символы кодируют одинаковым минимально возможным количеством бит. Код подразделения состоит из двух натуральных чисел, не превышающих 100, каждое из которых кодируется как двоичное число и занимает минимально возможное целое число бит. Личный код и код подразделения записываются подряд и вместе занимают минимально возможное целое число байт. Всего на пропуске хранится 32 байт данных. Сколько байт выделено для хранения дополнительных сведений об одном сотруднике? В ответе запишите только целое число — количество байт.
12. Тип 12 № 9764 ![]()
Исполнитель Редактор получает на вход строку цифр и преобразует её.
Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 127 идущих подряд цифр 9? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (333) ИЛИ нашлось (999)
ЕСЛИ нашлось (333)
ТО заменить (333, 9)
ИНАЧЕ заменить (999, 3)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
13. Тип 13 № 18588 ![]()
В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая — к адресу самого узла в этой сети. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого места — нули. Обычно маска записывается по тем же правилам, что и IP-адрес, — в виде четырёх байтов, причём каждый байт записывается в виде десятичного числа. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске.
Например, если IP-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.
Узлы с IP-адресами 98.162.71.151 и 98.162.71.155 находятся в разных сетях. Чему равно наименьшее количество возможных единиц в масках этих сетей?
14. Тип 14 № 47218 ![]()
Операнды арифметического выражения записаны в системе счисления с основанием 15:
123x515 + 1x23315.
В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 14. Для найденного значения x вычислите частное от деления значения арифметического выражения на 14 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
15. Тип 15 № 18566 ![]()
Для какого наименьшего целого неотрицательного числа A выражение
(3m + 4n 66) ∨ (m ≤ A) ∨ (n A)
тождественно истинно при любых целых неотрицательных m и n?
16. Тип 16 № 40732 ![]()
Обозначим остаток от деления натурального числа a на натуральное число b как a mod b.
Алгоритм вычисления значения функции F(n), где n — целое неотрицательное число, задан следующими соотношениями:
F(0) = 0;
F(n) = F(n − 1) + 1, если n 0 и при этом n mod 3 = 2;
F(n) = F((n − n mod 3) / 3), если n 0 и при этом n mod 3
Укажите наименьшее возможное n, для которого F(n) = 6.
17. Тип 17 № 45251 ![]()
В файле содержится последовательность натуральных чисел. Элементы последовательности могут принимать целые значения от 1 до 100 000 включительно. Определите количество пар последовательности, в которых хотя бы одно число делится на минимальный элемент последовательности, кратный 21. Гарантируется, что такой элемент в последовательности есть. В ответе запишите количество найденных пар, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
17.txt
Ответ:
18. Тип 18 № 27666 ![]()
Квадрат разлинован на N×N клеток (1 N
Задание 18
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 35 и 15.
19. Тип 19 № 27805 ![]()
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или четыре камня либо увеличить количество камней в куче в пять раз. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 19 или 75 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 63.
Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 63 или больше камней. В начальный момент в куче было S камней; 1 ≤ S ≤ 62.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, то есть не являющиеся выигрышными независимо от игры противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
20. Тип 20 № 27806 ![]()
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или четыре камня либо увеличить количество камней в куче в пять раз. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 19 или 75 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 63.
Победителем считается игрок, сделавший последний ход, то емть первым получивший кучу, в которой будет 63 или больше камней. В начальный момент в куче было S камней; 1 ≤ S ≤ 62.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, то есть не являющиеся выигрышными независимо от игры противника.
Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.
21. Тип 21 № 27807 ![]()
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или четыре камня либо увеличить количество камней в куче в пять раз. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 19 или 75 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 63.
Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 63 или больше камней. В начальный момент в куче было S камней; 1 ≤ S ≤ 62.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, то есть не являющиеся выигрышными независимо от игры противника.
Найдите минимальное значение S, при котором одновременно выполняются два условия:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
22. Тип 22 № 47598 ![]()
В файле 22_17.xlsx содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы — время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:
| ID процесса B | Время выполнения процесса B (мс) | ID процесса(ов) A |
|---|---|---|
| 1 | 4 | 0 |
| 2 | 3 | 0 |
| 3 | 1 | 1;2 |
| 4 | 7 | 3 |
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 — через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
23. Тип 23 № 18570 ![]()
Исполнитель РазДваТри преобразует число на экране.
У исполнителя есть три команды, которым присвоены номера.
1. Прибавить 1.
2. Умножить на 2.
3. Умножить на 3.
Первая команда увеличивает число на экране на 1, вторая умножает его на 2, третья умножает на 3.
Программа для исполнителя РазДваТри — это последовательность команд. Сколько существует программ, которые преобразуют исходное число 1 в число 50, и при этом траектория вычислений содержит число 14 и не содержит числа 16?
Траектория вычислений — это последовательность результатов выполнения всех команд программы. Например, для программы 312 при исходном числе 3 траектория будет состоять из чисел 9, 10, 20.
24. Тип 24 № 33494 ![]()
Текстовый файл содержит только заглавные буквы латинского алфавита (ABC…Z). Определите символ, который чаще всего встречается в файле сразу после буквы E.
Например, в тексте EBCEEBEDDD после буквы E два раза стоит B, по одному разу — E и D. Для этого текста ответом будет B.
Для выполнения этого задания следует написать программу. Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.
Задание 24
25. Тип 25 № 33104 ![]()
Назовём нетривиальным делителем натурального числа его делитель, не равный единице и самому числу. Например, у числа 6 есть два нетривиальных делителя: 2 и 3. Найдите все натуральные числа, принадлежащие отрезку [289123456; 389123456] и имеющие ровно три нетривиальных делителя. Для каждого найденного числа запишите в ответе его наибольший нетривиальный делитель. Ответы расположите в порядке возрастания.
Например, в диапазоне [5; 16] ровно три различных натуральных делителя имеет число 16, поэтому для этого диапазона вывод на экране должна содержать следующие значения:
16 8
Ответ:
26. Тип 26 № 40742 ![]()
Во многих компьютерных системах текущее время хранится в формате «UNIX-время» — количестве секунд от начала суток 1 января 1970 года.
В одной компьютерной системе проводили исследование загруженности. Для этого в течение месяца с момента UNIX-времени 1633046400 фиксировали и заносили в базу данных моменты старта и финиша всех процессов, действовавших в этой системе.
Вам необходимо определить, какое наибольшее количество процессов выполнялось в системе одновременно на неделе, начавшейся в момент UNIX-времени 1633305600, и в течение какого суммарного времени (в секундах) выполнялось такое наибольшее количество процессов.
Входные данные.
Задание 26
Первая строка входного файла содержит целое число N — общее количество процессов за весь период наблюдения. Каждая из следующих N строк содержит 2 целых числа: время старта и время завершения одного процесса в виде UNIX-времени. Все данные в строках входного файла отделены одним пробелом.
Если в качестве времени старта указан ноль, это означает, что процесс был активен в момент начала исследования. Если в качестве времени завершения указан ноль, это означает, что процесс не завершился к моменту окончания исследования.
При совпадающем времени считается, что все старты и завершения процессов происходят одновременно, в начале соответствующей секунды. В частности, если время старта одного процесса совпадает с временем завершения другого и других стартов и завершений в этот момент нет, то количество активных процессов в этот момент не изменяется.
В ответе запишите два целых числа: сначала максимальное количество процессов, которые выполнялись одновременно на неделе, начиная с момента UNIX-времени 1633305600, затем суммарное количество секунд, в течение которых на этой неделе выполнялось такое максимальное количество процессов.
Ответ:
27. Тип 27 № 35916 ![]()
В текстовом файле записан набор натуральных чисел, не превышающих 108. Гарантируется, что все числа различны. Из набора нужно выбрать три числа, сумма которых делится на 3. Какую наименьшую сумму можно при этом получить?
Входные данные.
Файл A
Файл B
Первая строка входного файла содержит целое число N — общее количество чисел в наборе. Каждая из следующих N строк содержит одно число.
Пример входного файла:
4
5
8
14
11 В данном случае есть четыре подходящие тройки: 5, 8, 11 (сумма 24); 5, 8, 14 (сумма 27); 5, 14 11 (сумма 30) и 8, 14, 11 (сумма 33). В ответе надо записать число 24.
Вам даны два входных файла (A и B), каждый из которых имеет описанную выше структуру. В ответе укажите два числа: сначала значение искомой суммы для файла A, затем для файла B.
Ответ:

 Получите свидетельство
Получите свидетельство Вход
Вход











 ЕГЭ 2025. Март Информатика Вариант 5 (76.22 KB)
ЕГЭ 2025. Март Информатика Вариант 5 (76.22 KB)
 1
1 280
280 1
1





ЕГЭ по инфороматике