Градусная и радианная меры угла. Вращательное движение.Синус, косинус, тангенс и котангенс.

Тригонометрия

Градусная и радианная меры угла. Вращательное движение. Синус, косинус, тангенс и котангенс.

Единицы измерения углов

Градусы

Радианы

Градусная мера угла

 =1 

1  – цена одного деления окружности, разделенной на 360 частей

Углом в 1 0 (один градус) называют центральный угол в окружности, опирающийся на круговую дугу, равную 1/360 части окружности.

На рисунке изображен угол β, равный 50 0 то есть этот угол опирается на круговую дугу размером 50/360 длины окружности.

Вся окружность состоит из 360 «кусочков» круговых дуг, или угол, описываемый окружностью, равен 360 0 .

R=1

R=1

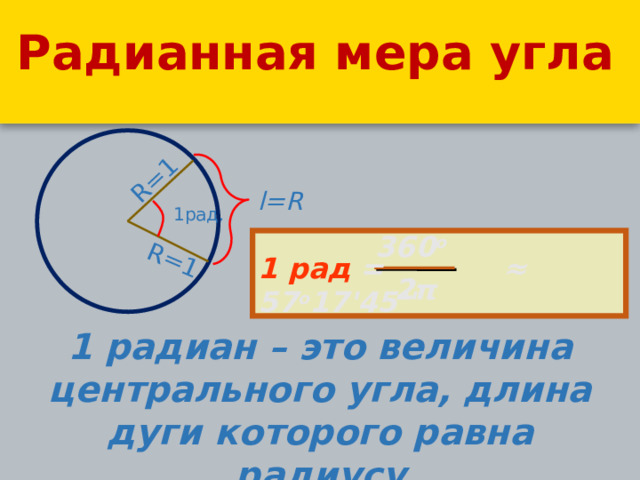
Радианная мера угла

l=R

1рад.

360 о

1 рад = ≈ 57 о 17'45''

2π

1 радиан – это величина центрального угла, длина дуги которого равна радиусу

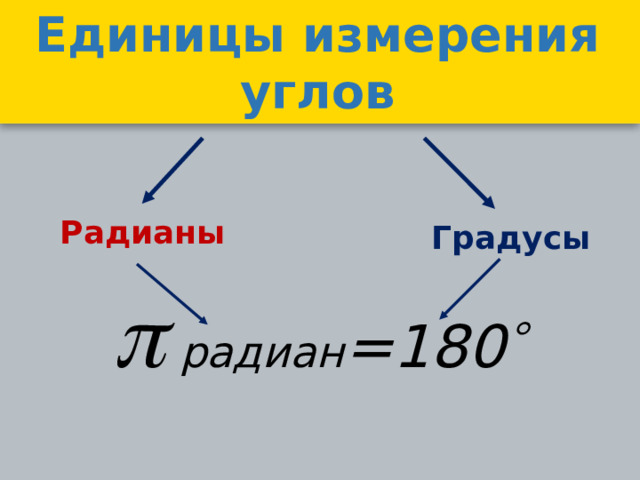
Единицы измерения углов

Радианы

Градусы

 радиан =180 

Перевод из градусной меры в радианную:

 радиан =180 



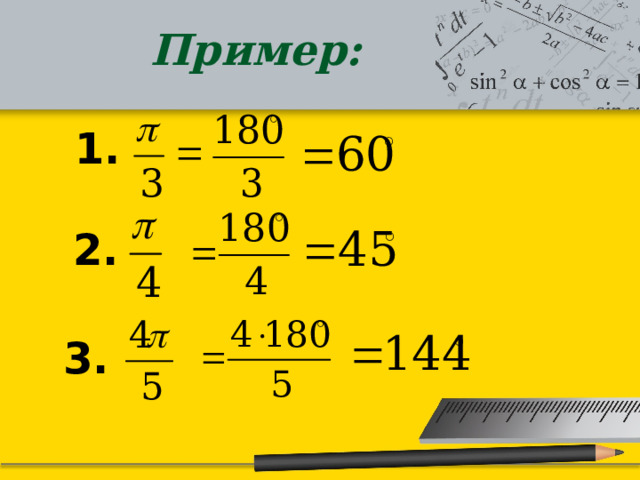
Пример:

1.

2.

3.

Перевод из радианной меры в градусную:

 радиан =180 



Пример:

1.

2.

3.

Окружность с радиусом, равным 1называется   единичной .

Данная окружность построена в декартовой системе координат. Радиус окружности равен единице, при этом центр окружности лежит в начале координат, начальное положение радиуса-вектора зафиксировано вдоль положительного направления оси x (в нашем примере, это радиус AB).

Единичная окружность r = 1

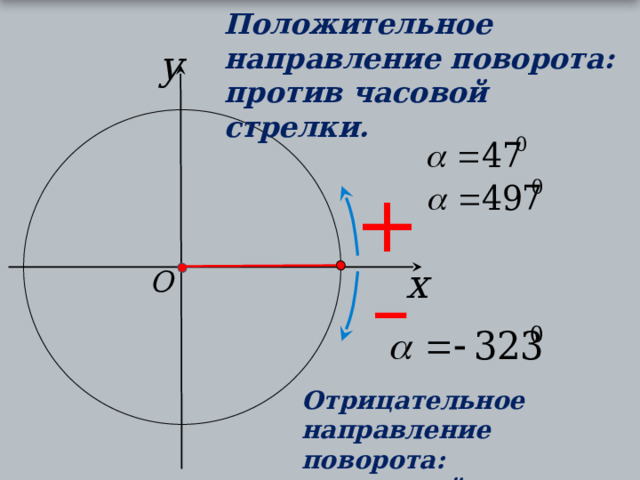
Положительное направление поворота:

против часовой стрелки.

y

+

x

–

O

.

Отрицательное направление поворота:

по часовой стрелке.

12

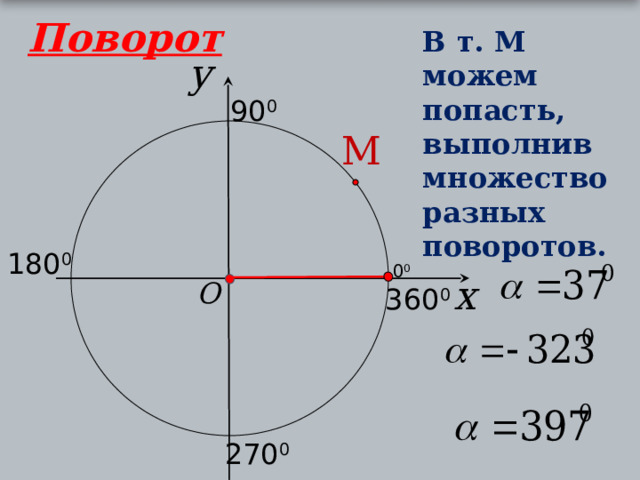
Поворот

В т. М можем попасть, выполнив множество разных поворотов.

y

90 0

M

180 0

0 0

x

O

360 0

.

270 0

13

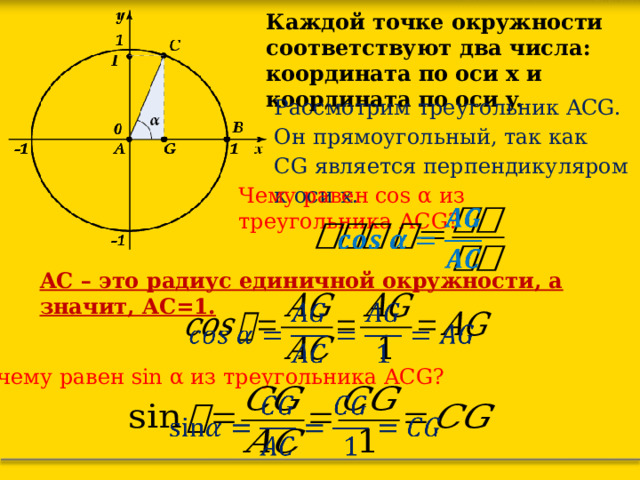
Каждой точке окружности соответствуют два числа: координата по оси x и координата по оси y.

Рассмотрим треугольник ACG. Он прямоугольный, так как CG является перпендикуляром к оси x.

Чему равен cos α из треугольника ACG?

AC – это радиус единичной окружности, а значит, AC=1.

А чему равен sin α из треугольника ACG?

А можно сказать, какие координаты имеет точка C, принадлежащая окружности?

А если сообразить, что cos α и sinα - это просто числа? Какой координате соответствует  sinα ?

Ну, конечно, координате x ! А какой координате соответствует  cos α ?

Все верно, координате y ! Таким образом, точка  C(x;y)=C(cosα;sinα).

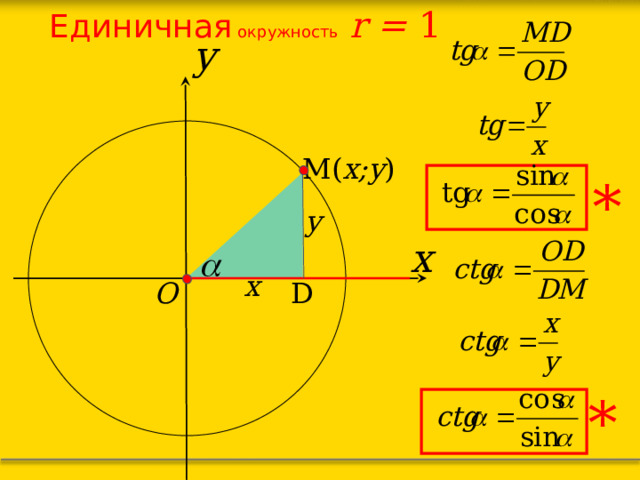
Единичная окружность r = 1

y

M( x;y )

*

y

x

x

D

O

*

16

Cинусом угла называется ордината y точки М, а косинусом угла – абсцисса x точки М.

x

cos

a

a

=

y;

sin

=

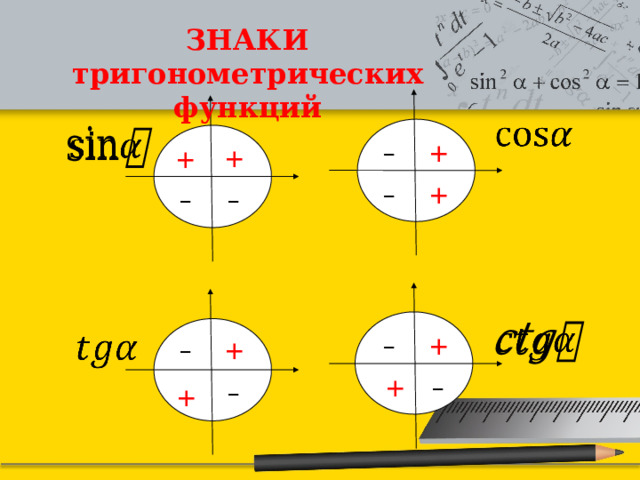
ЗНАКИ тригонометрических функций

–

+

+

+

–

+

–

–

+

–

–

+

+

–

–

+