Геометрическая прогрессия

Костромитина С. В.

«МАТЕМАТИКУ УЖЕ ЗАТЕМ НАДО УЧИТЬ, ЧТО ОНА УМ В ПОРЯДОК ПРИВОДИТ»

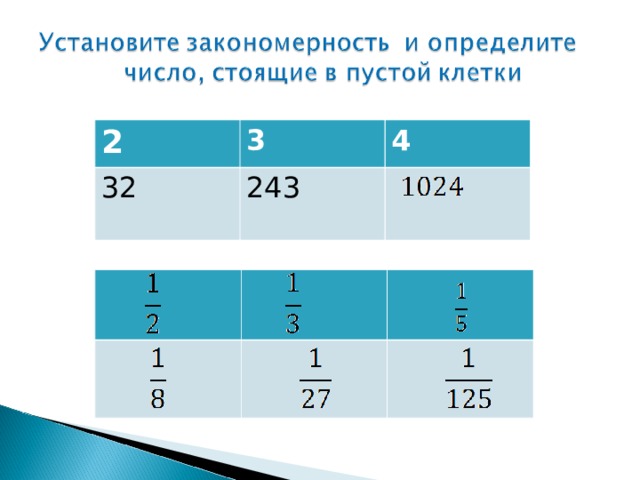
2

3

32

4

243

геометрическая

тоже

одно

член

второго

равен

число

каждый

отличных

которой

это

прогрессия

числовая

последовательность

члену

умноженному

на

от

предыдущему

со

начиная

нуля

и

чисел

1) Числовая последовательность 1,6; 0,8; … является геометрической прогрессией. Найти первый член прогрессии и знаменатель геометрической прогрессии.

Ответ: b 1 = 0,8 q = 2.

3) (b n ) – геометрическая прогрессия b 5 = 11; b 7 = =99. Найти знаменатель геометрической прогрессии.

Ответ: 9.

1) ( b n ) – геометрическая прогрессия. Найти b 4 , если b 1 = 2;

q = 3. (Д)

2) ( b n ) – геометрическая прогрессия. Найти b 2 , если b 1 =128 q= . (Е)

3) ( b n ) – геометрическая прогрессия. Найти b 1 , если b 5 = ;

q = . (А)

4 ) ( b n ) – геометрическая прогрессия. Найти следующий член прогрессии 0,2; 0,8; … . (Х)

5) ( b n ) – геометрическая прогрессия. Найти q, если b 2 = 32;

b 1 = 16. ( Р)

6) Поставьте между числами 3 и 81 два числа, чтобы вместе с данными числами получилась геометрическая прогрессия.

(И; М)

Древнегреческий ученый

неоднократно возвращался

к вопросу о вычислении

сумм прогрессий. В трактате

«О квадратуре параболы»

он рассматривает задачу

эквивалентную задаче о

нахождении суммы бесконечной убывающей прогрессии

Пусть (b n ) – геометрическая прогрессия.

S n = b 1 + b 2 + b 3 + … + b n |· q

S n · q = b 1 q + b 2 q + … + b n q

S n · q = b 2 + b 3 + … + b n q

S n · q – S n = ( b 2 + b 3 + … + b n q ) – ( b 1 + b 2 + b 3 + … + b n )

S n ( q – 1) = b 2 + b 3 + … + b n q – b 1 – b 2 – b 3 – … – b n

S n ( q – 1) = b n q – b 1)

Формула суммы n – первых членов геометрической прогрессии.

Формула суммы n – первых членов геометрической прогрессии.

Дано: Решение

(b n ) – геом. пр. S n = ; S 64 =

b 1 = 1

q = 2 = 18446744073709551615

S 64

18446744073709551615 зерен

Л.Н. Толстой, заинтересованный

этой легендой, подсчитал,

что данное количество

зерен соответствует

230584300921369 пудам

Такое количество зерен еще

не собранно человечеством

до нашего времени

Поднимает руки класс-это раз,

Повернулась голова-это два,

Руки вниз, вперед смотри – это три,

Руки в стороны пошире развернули -на четыре

С силой их к плечам прижать -это пять,

Всем ребятам надо сесть –это шесть.

1) Найти сумму шести первых членов геометрической прогрессии (b n ), в которой b 1 = 3; q = 2.

2) Найти сумму пяти первых членов геометрической прогрессии 1,5; – 3 … .

=

;

Дано: Решение

(b n ) – геом. пр. S n = ;

b 1 = 3 S 6 = = = 3 ∙ 63 =

= 189

q = 2

S 6 – ? Ответ: 189

1) Верно ли, что каждый член геометрической прогрессии равен предыдущему члену умноженному на одно и то же число?

2) Верно ли, что – формула n – го члена геометрической прогрессии?

3) Верно ли, что модуль любого члена геометрической прогрессии равен среднему геометрическому предыдущего и последующего членов?

4) Верно ли, что q = – формула знаменателя геометрической прогрессии?

5) Верно ли, что геометрическую прогрессию можно рассматривать как показательную функцию заданную на множестве натуральных чисел?

6) Верно ли, что – формула суммы n – первых

членов геометрической прогрессии?

7) Верно ли, что числовая последовательность

является геометрической прогрессией?

1) да

2) нет

3) да

4) да

5) да

6) нет

7) да

Устная работа

Зашифрованное задание

Решение задач

Верные и неверные утверждения

Итоговая оценка

Человек не знающий математики, не способен ни к каким другим наукам, более того он даже не способен оценить уровень своего невежества.

• На «3» №17.25в; №17.26в; № 17.28в,г
• На «4» +17.30
• На «5» + сочинение на тему: « Геометрическая прогрессия в природе и технике»