Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности

Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности

9 класс

Садовская Надежда Павловна

Устная работа

• Какой многоугольник называется правильным?
• Как найти угол правильного многоугольника?
• Сформулируйте следствия из теорем.
• Что вы понимаете под словами центр правильного многоугольника?
• Как найти площадь треугольника, зная радиус вписанной окружности?

Поверка домашнего задания

Дано:

Решение :

• ABCDE - правильный,
• ВО= 2
• Найти : А B

• Угол ЕАВ равен 108 ⁰, значит угол АВЕ равен 36⁰.
• Угол BAD равен 36⁰.
• Воспользуемся теоремой синусов: ВО/ sinA=AB/sinO из треугольника АВО.
• АВ=2*0.95:0.59=3.2

В

2

С

А

Ответ: 3.2

о

E

D

Вывод формулы площади правильного многоугольника

• Р - периметр многоугольника,
• r- радиус вписанной окружности

Основные формулы

Сторона правильного многоугольника

Радиус вписанной окружности

n=6

n=8

Запомните!

Работа в группах

• 1 группа Дано: R , n=3 . Найти а.
• 2 группа Дано : R, n=4. Найти а.
• 3 группа Дано : R, n=6. Найти а.
• 4 группа Дано : R , n=3 . Найти а.
• 5 группа Дано : R, n=4. Найти а.
• 6 группа Дан о: R, n=6. Найти а.

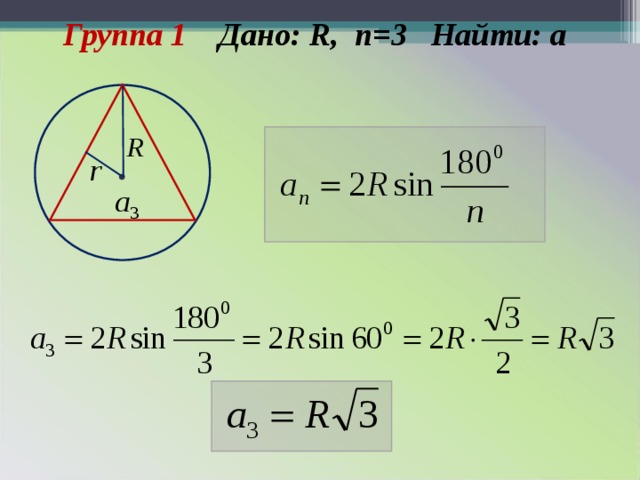
Группа 1 Дано: R , n =3 Найти: а

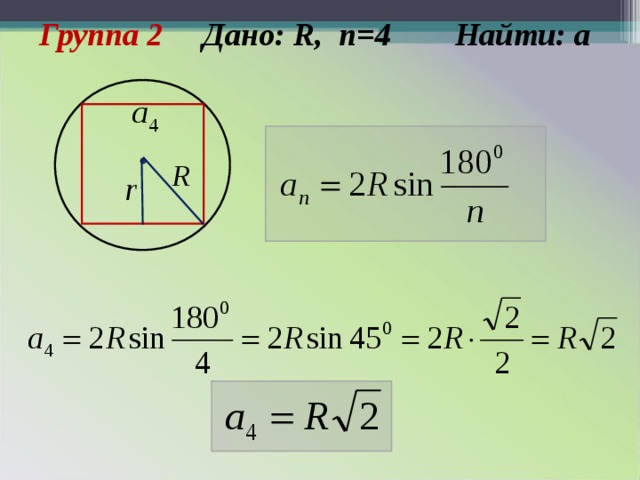
Группа 2 Дано: R , n =4 Найти: а

Группа 3 Дано: R , n =6 Найти: а

Новые формулы

Новые формулы

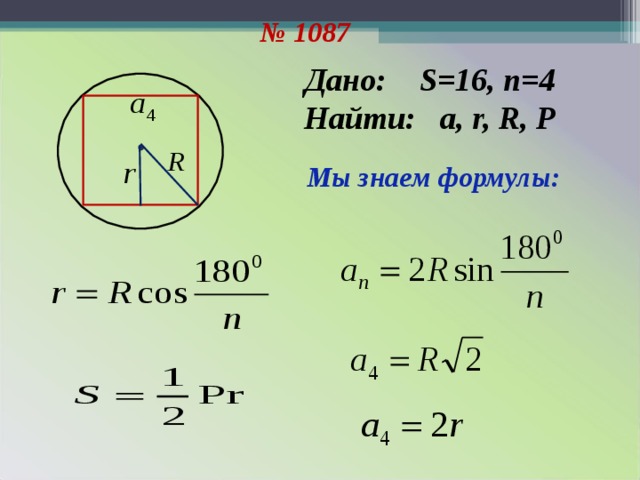
№ 1087

Дано: S=16 , n =4

Найти: a, r, R, P

Мы знаем формулы:

№ 1087 (1,2,3)

N

1

R

2

r

3

a 4

4

6

2

P

S

№ 1088( 5 )

Дано: P=6 , n = 3

Найти: R, a, r, S

Мы знаем формулы:

Подготовка к ОГЭ

• В треугольнике ABC угол А=40 ⁰, внешний угол при вершине В равен 102⁰. Найдите угол С.
• Средняя линия трапеции равна 25, а меньшее основание равно 17. Найдите большее основание.

Подведем итог

Мы знаем формулы:

• п.105-108 повторить;
• выучить формулы;
• № 1090, 1091, 1087(3)