| ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ТВЕРСКОЙ КОЛЛЕДЖ СЕРВИСА И ТУРИЗМА» _________________________________________________________________ 170037, г. Тверь, пр-т Победы, д. 49/21, тел/факс(4822) 58-52-80, e-mail: [email protected]
Методическая разработка
«Формирование системы развития метапредметных познавательных умений студентов средствами учебной дисциплины ПД. 01 Математика»
Преподаватель математики Нюхлякова Н.А.
г. Тверь 2018 г.
|
Содержание
| № | Оглавление | Стр. |
| 1 | Пояснительная записка | 3-4 |
| 2 | Методическое обеспечение формирования метапредметных познавательных умений по математике | 4-6 |
|
| 2.1 Задачи с практической направленностью | 4-5 |
|
| 2.2 Методы формирования метапредметных познавательных умений на уроках математики | 5 |
|
| 2.3 Приёмы для формирования метапредметных познавательных умений на уроках математики | 5-6 |
|
| 2.4 Образовательные технологии для формирования метапредметных познавательных умений на уроках математики | 6 |
| 3 | Этапы для формирования метапредметных познавательных умений на уроках математики | 6-7 |
| 4 | Результаты формирования метапредметных познавательных умений по математике | 7 |
| 5 | Система развития метапредметных познавательных умений средствами учебной дисциплины ПД.01 Математика | 7-10 |
| 6 | Проектная деятельность как средство формирования метапредметных познавательных умений по математике | 10-14 |
Пояснительная записка
В ФГОС нового поколения особое внимание уделено метапредметным познавательным умениям, поскольку именно они обеспечивают качественную подготовку студентов к самостоятельному решению проблем, с которыми встречается каждый человек на разных этапах своего жизненного пути в условиях быстро меняющегося общества. Метапредметный подход позволяет сформировать целостную личность студента, а так же обеспечить преемственность всех ступеней образования.
Познавательные УУД - включают действия исследования, поиска, отбора и структурирования необходимой информации, моделирование изучаемого содержания.
В познавательные универсальные действия выделяют общеучебные действия, логические, действия постановки и решения проблем (поисково-исследовательские)
Общеучебные:
формулирование познавательной цели;
поиск и выделение информации;
знаково-символические
моделирование
Логические:
обобщение
выделение главного
систематизация
классификация
сравнение
анализ с целью выделения признаков (существенных, несущественных)
синтез как составление целого из частей, восполняя недостающие компоненты;
установление причинно-следственных связей;
построение логической цепи рассуждений;
доказательство;
выдвижение гипотез и их обоснование.
Поисково-исследовательские:
исследовательские умения
Изучение математики направлено на достижение следующих целей в метапредметном направлении:
формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности.
Методическая разработка включает методическое обеспечение формирования метапредметных познавательных умений и их систему развития средствами учебной дисциплины «ПД.01 Математика».
Данную разработку могут использовать преподаватели при проведении практических занятий по математике и при разработке внеаудиторной самостоятельной работы.
2. Методическое обеспечение формирования метапредметных познавательных умений по математике
2.1 Задачи с практической направленностью.
Одним из направлений применения метапредметных познавательных умений в математике является усиление прикладной направленности, т.е. появление целого пласта задач практической направленности. Такого рода задачи появились в итоговых контрольно-измерительных материалах по математике (ЕГЭ), это задачи на умение использовать приобретённые математические знания в повседневной жизни. Данные задания позволяют развить метапредметные познавательные умения, показать связь математики с жизнью, что обуславливает усиление мотивации к изучению самого предмета.
Примеры классов задач такого рода.
Задачи по теме «Энергосбережение». В них нужно посчитать сумму оплаты семьи за израсходованную электроэнергию. В условиях предлагаются текущие и прошлые показания счётчика, а также стоимость одного киловатта электроэнергии. Причём в задачах ЕГЭ разграничивается тариф на дневной и ночной.
Задачи на тему покупок. В них нужно посчитать: количество объектов, при заданной сумме имеющихся денег и цене товара, количество объектов при возрастании или снижении цены на определённое количество процентов.
Задачи на нахождение количества лекарства необходимого выпить больному, когда известна ежедневная доза необходимая больному.
Задачи статистического характера о нахождение группы жителей, по известному количеству всех жителей и процентному составу различных групп.
Задачи экономического характера о банковских вкладах или кредитах с известной процентной ставкой.
Задачи на умение использовать графики зависимостей в повседневной жизни (читать графики). Обычно такие графики строятся с использованием наблюдений за погодой, статистических наблюдений за продажами на фондовом рынке, зависимости пропорциональных физических величин, а также ходе химических реакций.
Задачи маркетингового характера. В них необходимо из предложенных вариантов, выбрать самый оптимальный. Это задачи связанные и с продуктовыми корзинами, и с покупкой определённых строительных товаров, и рейтингом бытовых приборов.
Прикладные задачи с физическим или экономическим смыслом. В этих задачах дана не графическая интерпретация некоторых зависимостей одной величины от другой, а показана функциональная зависимость этих величин. Например, в них нужно отыскать месячный объём производства при известных затратах и сумме прибыли, или найти время движения объекта по известному закону движения и т.д.
2.2 Методы формирования метапредметных познавательных умений на уроках математики:
Метод проблемного изложения. Сначала совместно со студентами обозначается проблемная ситуация, затем студентом аргументируется каждый шаг к решению проблемы.
Эвристическая беседа – это система логически взаимосвязанных вопросов преподавателя и ответов студентов. Она способствует непроизвольному формированию памяти и навыков анализа и преобразования понятий, а также желания общаться, быть причастным к решению задач, работе всего коллектива.
Исследовательский метод. Используется при организации практических занятий по математике, на обобщающих уроках, когда студенты достаточно хорошо знают материал, что позволяет им поставить задачу и найти ее решение.
2.3 Приёмы для формирования метапредметных познавательных умений на уроках математики:
Групповая работа. Заключается в следующем: преподаватель разбивает класс на малые группы, при этом не проводится четкого распределения ролей, студенты выбирают их сами.
Уточнение выбора роли означает дальнейшее повышение ответственности за свой выбор, так как результат работы зависит от каждого.
Участие студента в работе группы должно быть добровольным и сознательным.
При использовании групповой работы формируются навыки построения внутри коллективных отношений.
Самой интересной формой групповой работы является мозговой штурм. Основная задача приёма – сбор как можно большего числа идей, в результате чего участники обсуждения освобождаются от инерции мышления и стереотипов.
Работа в парах. Работа в парах – это форма организации деятельности студента на уроке, которая обучает учебному сотрудничеству. Используя этот приём, преподаватель вместе со студентами определяет правила работы в паре для эффективного взаимодействия. При этом студенты учатся слушать друг друга, совместно вырабатывая общее решение.
2.4 Образовательные технологии для формирования метапредметных познавательных умений на уроках математики:
уровневая дифференциация
ИКТ
проектная деятельность
проблемное обучение
технологии критического мышления
обучение в сотрудничестве
3. Этапы для формирования метапредметных познавательных умений на уроках математики
1-этап - вводно - мотивационный.
Чтобы студент начал «действовать», необходимы определенные мотивы. На уроках математики необходимо создать проблемные ситуации, где студент проявляет умение комбинировать элементы для решения проблемы. На этом этапе студенты должны осознать, почему и для чего им нужно изучать данную тему, и изучить, какова основная учебная задача предстоящей работы. (Используется технология проблемного обучения)
2- этап - открытие математических знаний.
На данном этапе решающее значение имеют приемы, требующие самостоятельных исследований, стимулирующие рост познавательной потребности.
3- этап - формализация знаний.
Основное назначение приемов на этом этапе - организация деятельности студентов, направленная на всестороннее изучение установленного математического факта.
4- этап - обобщение и систематизация.
На этом этапе применяются приемы, которые устанавливают связь между изученными математическими фактами, приводят знания в систему. Формирование всех составляющих учебно-познавательной компетентности происходит в процессе осуществления учебно-познавательной деятельности, соотносится с этапами ее формирования, т.е. носит деятельностный характер.
4. Результаты формирования метапредметных познавательных умений по математике
Результатом формирования метапредметных познавательных умений будет являться умение студента:
выделять тип задач и способы их решения
осуществлять поиск необходимой информации, которая нужна для решения задач
различать обоснованные и необоснованные суждения
обосновывать этапы решения учебной задачи
производить анализ и преобразование информации
проводить основные мыслительные операции (анализ, синтез, классификации, сравнение, аналогия и т.д.)
устанавливать причинно-следственные связи
владеть общим приемом решения задач
создавать и преобразовывать схемы необходимые для решения задач
осуществлять выбор наиболее эффективного способа решения задачи исходя из конкретных условий
5. Система развития метапредметных познавательных умений средствами учебной дисциплины ПД.01 Математика
Метапредметные познавательные умения по математике развиваются на протяжении всего курса изучения учебной дисциплины. На практических занятиях по математике задачи подбираются таким образом, чтобы уровень сложности возрастал по мере изучения нового материала, а метапредметные познавательные умения развивались в течение всего учебного курса.
Приоритетные метапредметные познавательные умения по учебной дисциплине ПД.01 Математика:
Умение сравнивать
Умение проводить доказательство
Умение проводить исследование
В приложенной таблице указано, как познавательные умения развиваются на протяжении всего учебного курса на примерах математических задач.
| Математика Умение | Начало учебного курса | Середина учебного курса | Завершение учебного курса |
| Умение сравнивать | Умение сравнивать числовые значения выражений. | Умение сравнивать значения тригонометрических функций. | Умение сравнивать значения производных функций в заданной точке. |
| Задание (Действительные числа, I курс) Сравнить числовые значения выражений: 1. 2.
| Задание (Тригонометрические функции, I курс) Используя свойство возрастания и убывания тригонометрических функций, сравнить числа: 1. cos 2. sin(- 3. tg(- | Задание (Производная и её геометрический смысл, II курс) Сравнить значения производных функций в заданной точке x0: 1. f(x)=-x3+x2 f(x)=x3-2x x0=2 2. f(x)=2x- f(x)= x0=1 3. f(x)=cos( f(x)=sin( | |
| Умение сравнивать площади многогранников. | Умение сравнивать площади круглых тел. | Умение сравнивать объёмы многогранников и круглых тел. | |
| Задание (Многогранники, I курс) Ребро куба и ребро правильного икосаэдра равны 10 см. Площадь поверхности какого многогранника будет больше? | Задание (Цилиндр, конус, шар, I курс) Прямоугольный треугольник с катетами 3 см и 4 см в первый раз вращается вокруг большего катета, а во второй – вокруг меньшего. Сравните площади боковых поверхностей получающихся при этом конусов. | Задание (Объёмы тел, I курс) Равнобочная трапеция с основаниями 12 см и 24 см и высотой 8 см в первый раз вращается около меньшего основания, а во второй – около большего. Сравните объёмы тел вращения. | |
| Умение проводить доказательство | Умение доказывать свойства непериодических функций. | Умение доказывать свойства периодических функций. | Умение доказывать свойства любых функций с использованием производной. |
| Задание (Показательная функция, I курс) Доказать, что графики функций | Задание (Тригонометрические функции, I курс) Доказать, что функция y=f(x) является периодической с периодом Т. 1. 2. 3. 4.
| Задание (Применение производной к исследованию функций, II курс) Доказать, что функция | |
| Умение доказывать равносильность линейных и квадратных уравнений и неравенств. | Умение доказывать равносильность тригонометрических уравнений. | Умение доказывать равносильность дифференциальных уравнений. | |
| Задание (Степенная функция, I курс) Доказать равносильность уравнений: 1. 2. Доказать равносильность неравенств: 1. 2.
| Задание (Тригонометрические уравнения, I курс) Доказать равносильность тригонометрических уравнений: 1. 2. 3. | Задание (Производная и её геометрический смысл, II курс) Доказать равносильность уравнений 1. 2. | |
| Умение проводить исследование
| Умение исследовать свойства степенных, показательных, логарифмических функций. | Умение исследовать свойства тригонометрических и обратных тригонометрических функций. | Умение исследовать свойства любых функций с помощью их производных. |
| Задание (Степенная функция, показательная функция, логарифмическая функция, I курс) Исследовать свойства функций: 1. 2. 3. | Задание (Тригонометрические функции, I курс) Исследовать свойства функций: 1. 2. 3. | Задание (Применение производной к исследованию функций,II курс) Исследовать свойства функций: 1. 2. 3. | |
| Умение исследовать взаимное расположение двух прямых в пространстве. | Умение исследовать взаимное расположение прямой и плоскости. | Умение исследовать взаимное расположение плоскости и круглого тела. | |
| Задание (Параллельность прямых и плоскостей, I курс) Отрезки AB и CD лежат в двух пересекающихся плоскостях α и β. Исследуйте взаимное расположение прямых AD и BC.
| Задание (Перпендикулярность прямых и плоскостей, I курс) Прямая а перпендикулярна к плоскости α и перпендикулярна к прямой в, не лежащей в этой плоскости. Исследуйте взаимное расположение прямой в и плоскости α. | Задание (Цилиндр, конус, шар, II курс) Исследуйте взаимное расположение сферы и плоскости в зависимости от соотношения между радиусом сферы и расстоянием от её центра до плоскости. |
6. Проектная деятельность как средство формирования метапредметных познавательных умений по математике
Метод проектов - способ организации самостоятельной работы студентов, который собирает в себе исследовательские, рефлексивные, проблемные групповые методики работы. Проекты по математике могут быть как небольшими, рассчитанными на один урок, так и достаточно объёмными, требующими от студентов внеурочной подготовки. Как показывает практика, авторы наиболее интересных, неординарных проектов по математике обладают более высокими показателями метапредметных показательных умений. Метод проектов создаёт сильную мотивацию к обучению и самообразованию. Хорошо разрабатываются проекты, связывающие математику с практической деятельностью человека: «Исследование формулы объёма продукции, произведённой за промежуток времени на производстве», «Определение возможностей практического применения логарифмической функции», «Выявление возможностей использования математики в архитектуре».
В процессе проектной деятельности формируется студент, умеющий действовать не только по образцу, но и самостоятельно получающий необходимую информацию из максимально большего числа источников, умеющий ее анализировать, выдвигать гипотезы, строить модели, экспериментировать и делать выводы, принимать решения в сложных ситуациях.
Применение метода проектов имеет большие преимущества.
Во-первых, он способствует успешной социализации выпускников за счет создания адекватной информационной среды, в которой студенты учатся ориентироваться самостоятельно. Выходя за рамки учебных программ, этот метод заставляет студентов обращаться не только к справочной литературе, но и к Интернет-ресурсам, и к электронным источникам. А это приводит к формированию личности, обладающей информационной культурой в целом.
Во-вторых, актуальность тем исследования, возможность ярко, наглядно познакомить с результатами своих поисков широкую аудиторию позволяют организовать процесс познания, поддерживающий деятельностный подход к обучению на всех его этапах. Развиваются творческие способности студентов.
В-третьих, студенты осваивают технологию проведения исследования.
В-четвертых, выбирая проблему исследования и решая конкретную задачу внутри группы, студенты исходят из своих интересов и степени подготовленности. Это создает возможность построения открытой системы образования, обеспечивающей каждому студенту собственную траекторию обучения и самообучения, а также дифференциацию и индивидуализацию образовательного процесса.
В приложенной таблице указано, как метапредметные познавательные умения развиваются на протяжении всей работы над проектом.
Тема проекта «Определение возможностей практического применения логарифмической функции»
| Математика Умение | Начало работы над проектом | Середина работы над проектом | Завершение работы над проектом |
| Умение проводить исследование | Умение исследовать свойства логарифмической функции | Умение исследовать прикладное значение логарифмической функции в следующих областях естествознания: географии, биологии, химии, физике, астрономии. | Умение исследовать прикладное значение логарифмической функции в экономике банковского дела. |
| Умение проводить доказательство | Умение доказать свойства логарифмической функции.
| 1. Умение доказать применение логарифмической функции в географии на примере решения следующих задач: Задача №1 По данным газеты «Зори» от 12 апреля 2011 года из доклада П. Е. Шишкина население в городе Старый Оскол за один год увеличилось с 256100 человек до 257135 человек. Через сколько лет население этого города увеличится в 1,5 раза? Задача №2 Альпинисты, поднимаясь на пик Победы, достигли высоты, где давление было равно 304 мм рт. ст. Вычислить, на какой высоте находились альпинисты. 2. Умение доказать применение логарифмической функции в биологии на примере решения задачи: Задача №3 В начальный момент времени было 8 бактерий, через 2 ч после помещения бактерий в питательную среду их число возросло до 100. Через сколько времени с момента помещения в питательную среду следует ожидать колонию в 500 бактерий? 3. Умение доказать применение логарифмической функции в химии на примере решения следующих задач: Задача №4 На сколько градусов надо повысить температуру для ускорения химической реакции в 59000 раз, если скорость реакции растёт в геометрической прогрессии со знаменателем, равным 3 при повышении температуры на каждые 10 Задача №5 Известно, что соотношение между углеродом C12 и его радиоактивным изотопом C14 во всех живых организмах постоянно. Период полураспада углерода C14 составляет 5760 лет. Определите возраст останков мамонта, найденных в вечной мерзлоте на Таймыре, если относительное содержание изотопа C14 в них составляет 26% от его количества в живом организме. 4. Умение доказать применение логарифмической функции в астрономии на примере решения следующих задач: Задача №6 До какой величины можно увидеть звёзды через телескоп, диаметр объектива которого равен 8 см? Задача №7 Во сколько раз Капелла ярче Денеба? 5. Умение доказать применение логарифмической функции в физике на примере решения следующих задач: Задача №8 Во сколько раз возрастет громкость звука, если вместо одной скрипки будут играть десять?
| 1. Умение доказать применение логарифмической функции в экономике банковского дела на примере решения следующих задач: Задача №9 Пусть вкладчик положил в банк 10000 руб. под ставку 12% годовых. Через сколько лет его вклад удвоится? Задача №10 Некоторая сумма денег в A руб. подвержена приросту в P% годовых. Через сколько лет эта сумма составит S руб.? Задача №11 Пусть в начальный момент времени имелось q единиц некоторого компонента, В некоторый другой момент времени t имеющийся компонент изменился в p раз. Установите, через какой промежуток времени (начиная с начального момента) этот компонент достигнет заданного количества B единиц.
|
Тема проекта «Исследование формулы объёма продукции, произведённой за промежуток времени на производстве»
| Математика Умение | Начало работы над проектом | Середина работы над проектом | Завершение работы над проектом |
| Умение проводить исследование | Умение исследовать формулы объема продукции по известной функции производительности труда и по известной производственной функции. | Умение исследовать прикладное значение формулы объёма продукции. | Умение исследовать, как формула объема продукции позволяет провести экономический анализ задачи |
| Умение проводить доказательство | Умение доказывать формулы объема продукции по известной функции производительности труда и по известной производственной функции. | Умение доказать значимость формулы объёма продукции на примерах решения экономических задач на нахождение объема продукции по известной функции производительности труда. Задача № 1. Пусть f(t)=-3t2+18t — производительность труда. Определить выработку рабочего: а) за весь рабочий день; б) за третий час работы; в) за последний час работы, если продолжительность рабочего дня 6 часов; г) провести экономический анализ задачи. Задача № 2. Изменение производительности производства с течением времени от начала внедрения нового технологического процесса задается функцией где t - время в месяцах. Найти объем продукции, произведенной за третий месяц. Задача № 3. Найти объем продукции выпущенной в течение года, считая количество рабочих дней равным 240, если производительность труда рабочего выражается функцией y=-0,0033x2-0,089x+20,96. Задача № 4. Найти объем продукции, произведенной рабочим за четвертый час рабочего дня, если производительность труда характеризуется следующей функцией: | Умение доказать значимость формулы объёма продукции на примерах решения экономических задач на нахождение объема продукции по известной производственной функции. Задача № 5. Найти объем продукции Q, произведенный за 4 года, если функция Кобба-Дугласа имеет вид: Задача № 6. Дана производственная функция y=2,4 L0,3K0,7, где y - объём товарной продукции в стоимостном выражении; L - фонд заработной платы; K - стоимость основных фондов. Произошло изменение используемых ресурсов: фонд заработной платы L уменьшился на 3 %, стоимость основных фондов K возросла на 5 %.
|
Таким образом, применение проектной деятельности в учебном процессе формирует метапредметные познавательные умения по математике, включающие в себя умение решать постоянно возникающие новые, нестандартные проблемы; соответствовать предъявляемым повышенным требованиям к коммуникационному взаимодействию и сотрудничеству, толерантности.

 Получите свидетельство
Получите свидетельство Вход
Вход



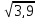 +
+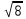 и
и 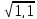 +
+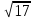
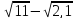 и
и 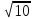 -
-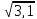
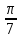 и cos
и cos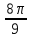
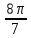 ) и sin(-
) и sin(-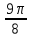 )
)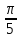 ) и tg(-
) и tg(-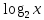 ,
,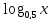 -3x
-3x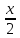 -1)+e3x, x0=2 и
-1)+e3x, x0=2 и 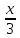 -3)+2x, x0=3
-3)+2x, x0=3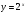 и
и 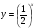 симметричны относительно оси ординат.
симметричны относительно оси ординат.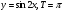
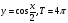
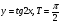
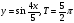
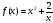 возрастает на промежутке
возрастает на промежутке 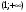 , убывает на промежутках
, убывает на промежутках 








 Формирование системы развития метапредметных познавательных умений студентов средствами учебной дисциплины ПД. 01" Математика" (96.67 KB)
Формирование системы развития метапредметных познавательных умений студентов средствами учебной дисциплины ПД. 01" Математика" (96.67 KB)
 0
0 157
157 1
1 Нравится
0
Нравится
0


