Формализация понятия алгоритма

Формализация понятия алгоритма

Алгоритм

• Алгоритм – это точно определенная инструкция, последовательно применяя которую к исходным данным, можно получить решение задачи.

• Для каждого алгоритма есть некоторое множество объектов, допустимых в качестве исходных данных.

Свойства алгоритма

• Массовость;
• Детерминированность;
• Результативность;
• Определенность.

Массовость

• Массовость - возможность применять многократно один и тот же алгоритм. Алгоритм служит, как правило, для решения не одной конкретной задачи, а некоторого класса задач. Так алгоритм сложения применим к любой паре натуральных чисел.

Детерминированность

• При применении алгоритма к одним и тем же исходным данным должен получаться всегда один и тот же результат, поэтому, например, процесс преобразования информации, в котором участвует бросание монеты, не является детерминированным и не может быть назван алгоритмом.

Результативность.

• Выполнение алгоритма должно обязательно приводить к его завершению. В то же время можно привести примеры формально бесконечных алгоритмов, широко применяемых на практике.

Определенность.

• На каждом шаге алгоритма у исполнителя должно быть достаточно информации, чтобы его выполнить. Кроме того, исполнителю нужно четко знать, каким образом он выполняется. Шаги инструкции должны быть достаточно простыми, элементарными, а исполнитель должен однозначно понимать смысл каждого шага последовательности действий, составляющих алгоритм. Поэтому вопрос о выборе формы представления алгоритма очень важен. Фактически речь идет о том, на каком языке записан алгоритм.

Формы представления алгоритмов.

• Одним из распространенных способов записи алгоритмов является запись на языке блок-схем. Запись представляет собой набор элементов (блоков), соединенных стрелками. Каждый элемент – это «шаг» алгоритма. Элементы блок-схемы делятся на два вида. Элементы, содержащие инструкцию выполнения какого-либо действия, обозначают прямоугольниками, а элементы, содержащие проверку условия – ромбами. Из прямоугольников всегда выходит только одна стрелка (входить может несколько), а из ромбов – две (одна из них помечается словом «да», другая – словом «нет», они показывают, соответственно, выполнено или нет проверяемое условие).

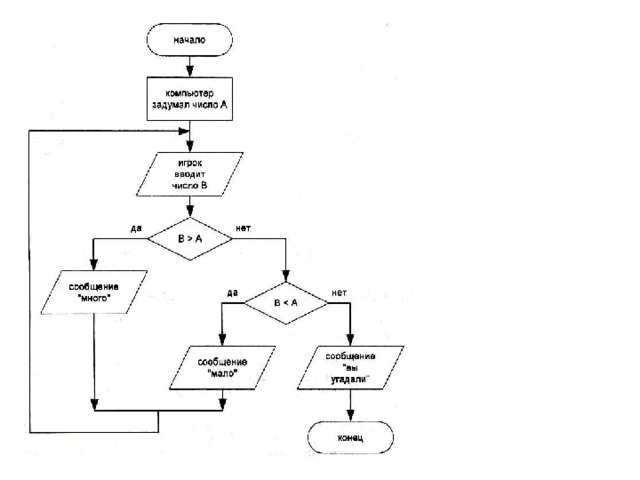
пример

Формализация понятия алгоритма. Теория алгоритмов

• В теории алгоритмов предполагается, что каждый шаг алгоритма таков, что его может выполнить достаточно простое устройство (машина), Желательно, чтобы это устройство было универсальным, т.е. чтобы на нем можно было выполнять любой алгоритм. Механизм работы машины должен быть максимально простым по логической структуре, но настолько точным, чтобы эта структура могла служить предметом математического исследования. Впервые это было сделано американским математиком Эмилем Постом в 1936 (машина Поста) еще до создания современных вычислительных машин и (практически одновременно) английским математиком Аланом Тьюрингом (машина Тьюринга).

Теория алгоритмов (Продолжение)

• История конечных автоматов: машина Поста и машина Тьюринга. Машина Поста – абстрактная вычислительная машина, предложенная Постом (Emil L.Post), которая отличается от машины Тьюринга большей простотой. Обе машины «эквивалентны» и были созданы для уточнения понятия «алгоритм».

Машина поста

• Абстрактная машина Поста представляет собой бесконечную ленту, разделенную на одинаковые клетки, каждая из которых может быть либо пустой, либо заполненной меткой «V». У машины есть головка, которая может перемещаться вдоль ленты на одну клетку вправо или влево, наносить в клетку ленты метку, если этой метки там ранее не было, стирать метку, если она была, либо проверять наличие в клетке метки. Информация о заполненных метками клетках ленты характеризует состояние ленты, которое может меняться в процессе работы машины. В каждый момент времени головка находится над одной из клеток ленты и, как говорят, обозревает ее. Информация о местоположения головки вместе с состоянием ленты характеризует состояние машины Поста.

Машина поста (продолжение)

• Работа машины Поста заключается в том, что головка передвигается вдоль ленты (на одну клетку за один шаг) влево или вправо, наносит или стирает метки, а также распознает, есть ли метка в клетке в соответствии с заданной программой, состоящей из отдельных команд.

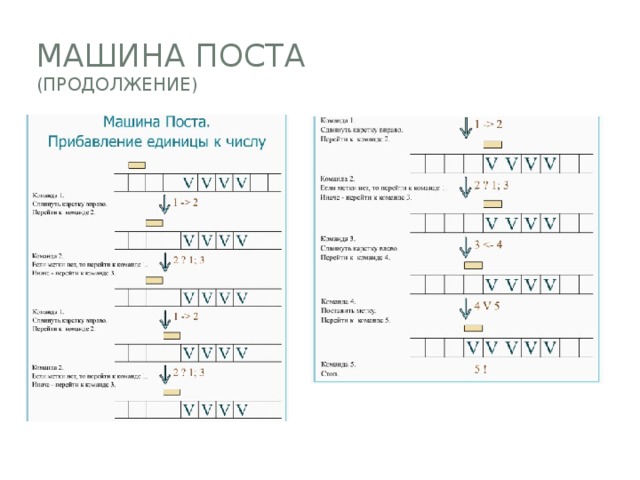
Машина поста (продолжение)

Машина тьюринга

• Машина Тьюринга состоит из счетной ленты (разделенной на ячейки и ограниченной слева, но не справа), читающей и пишущей головки, лентопротяжного механизма и операционного исполнительного устройства, которое может находиться в одном из дискретных состояний q0, q1, …, qs , принадлежащих некоторой конечной совокупности (алфавиту внутренних состояний), при этом q0 называется начальным состоянием. Читающая и пишущая головка может читать буквы рабочего алфавита A = {a0, a1, …, at }, стирать их и печатать.
• Каждая ячейка ленты в каждый момент времени занята буквой из множества А. Чаще всего встречается буква а0 – «пробел».
• Головка находится в каждый момент времени над некоторой ячейкой ленты – текущей рабочей ячейкой.
• Лентопротяжный механизм может перемещать ленту так, что головка оказывается над соседней ячейкой ленты, при этом возможна ситуация выхода за левый край ленты, которая является аварийной (недопустимой), или машинного останова, когда машина выполняет предписание об остановке

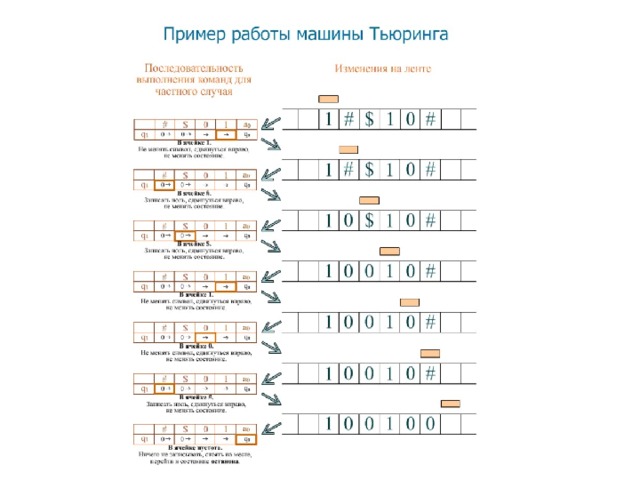
Основные элементы блок-схем

Существует несколько способов записи алгоритмов.

Алгоритм может быть записан на

• естественном языке
• в виде блок-схемы
• на алгоритмическом языке

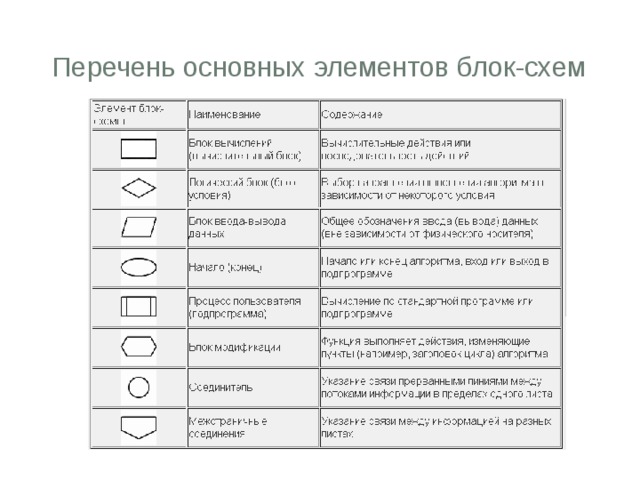
Перечень основных элементов блок-схем

требования к алгоритму

Составление алгоритмов и вопросы их существования являются предметом серьезных математических исследований. Алгоритм должен удовлетворять определенным требованиям. Принято выделять следующие семь:

• Наличие ввода исходных данных.
• Наличие вывода результата выполнения.
• Однозначность (компьютер «понимает» только однозначные инструкции).

требования к алгоритму

• Общность – алгоритм предназначен для решения некоторого класса задач.
• Корректность – алгоритм должен давать правильное решение задачи.
• Конечность – решение задачи должно быть получено за конечное число шагов.
• Эффективность – для решения задачи должны использоваться ограниченные ресурсы компьютера (процессорное время, объем оперативной памяти и т.д.).

Алгоритмическая структура

Суть решения задачи в переходе от исходной модели к прогнозируемому результату, через конечное число действий.

Несмотря на многообразие алгоритмов все они строятся из 3-х типов алгоритмических структур.

Линейным алгоритмом называется алгоритмом, в котором все указанные в последствии действия исполняются и притом только один раз.

Разветвляющимся алгоритмом называется алгоритм, в котором выполняется одна из ветвей действий при заданных значениях параметра.

Циклический алгоритм – алгоритм в котором какая-то совокупность действий повторяется несколько раз при изменяющихся значениях параметра.

Принципы разработки алгоритмов

Типы алгоритмических процессов

По структуре выполнения алгоритмы и программы делятся на три вида:

• Линейные
• Ветвящиеся
• Циклические

Линейный алгоритм

• Линейный алгоритм (линейная структура) – это такой алгоритм, в котором все действия выполняются последовательно друг за другом и только один раз. Схема представляет собой последовательность блоков, которые располагаются сверху вниз в порядке их выполнения. Первичные и промежуточные данные не оказывают влияния на направление процесса вычисления.

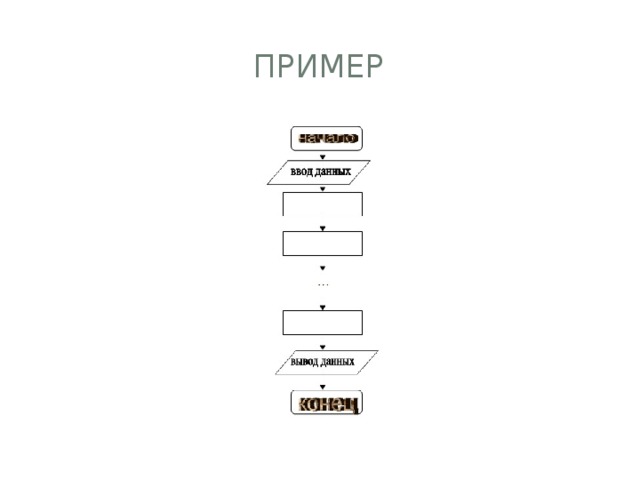
пример

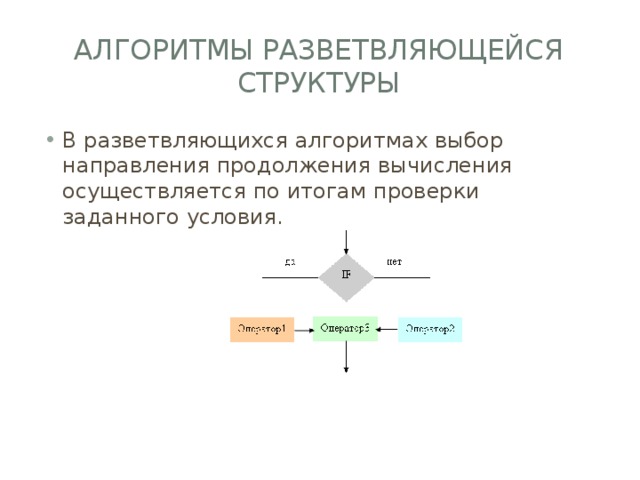
Алгоритмы разветвляющейся структуры

• В разветвляющихся алгоритмах выбор направления продолжения вычисления осуществляется по итогам проверки заданного условия.

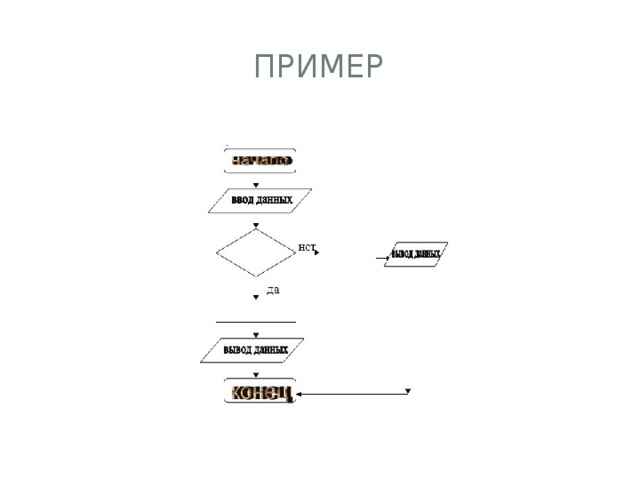
пример

Циклический алгоритм

• Для решения многих задач характерно многократное повторение отдельных участков вычислений. Для решения таких задач применяются алгоритмы циклической структуры (циклические алгоритмы). Цикл – последовательность команд, которая повторяется до тех пор, пока не будет выполнено заданное условие. Циклическое описание многократно повторяемых процессов значительно снижает трудоемкость написания программ. .

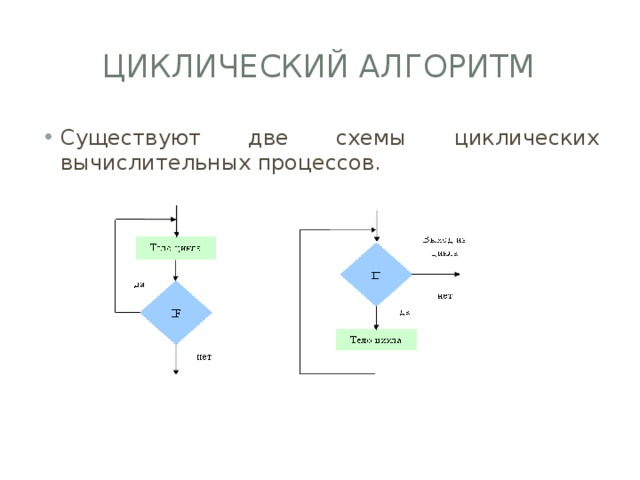
Циклический алгоритм

• Существуют две схемы циклических вычислительных процессов.

Циклический алгоритм

• Особенностью первой схемы является то, что проверка условия выхода из цикла проводится до выполнения тела цикла. В том случае, если условие выхода из цикла выполняется, то тело цикла не выполняется ни разу.
• Особенностью второй  схемы является то, что цикл выполняется хоты бы один раз, так как первая проверка условия выхода из цикла осуществляется после того, как тело цикла выполнено.
• Существуют циклы с известным числом повторений и итерационные циклы. При итерационном цикле выход из тела цикла, как правило, происходит при достижении заданной точности вычисления.

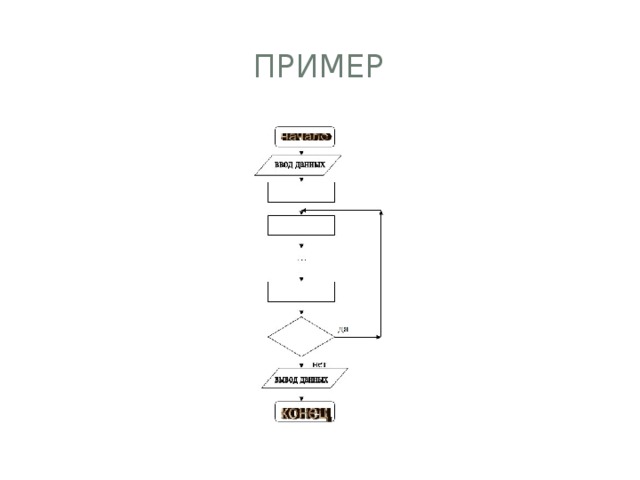
пример

Структуры алгоритма

Алгоритм любой сложности может быть представлен комбинацией трех базовых структур:

• следование;
• ветвление (в полной и сокращенной форме);
• цикл (с предусловием или постусловием).

Характерной особенностью этих структур является наличие у них одного входа и одного выхода.

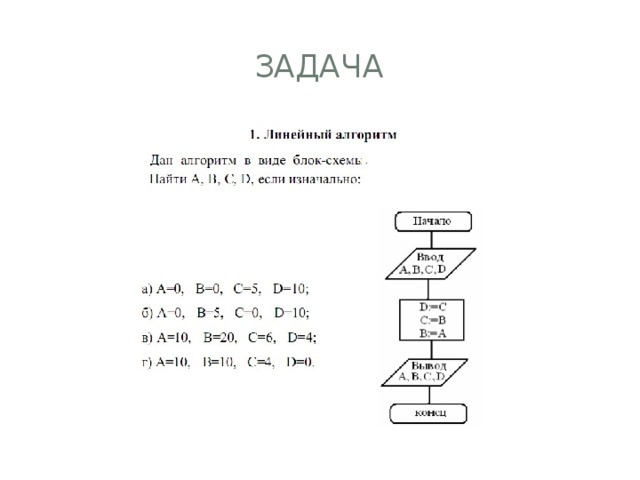
задача

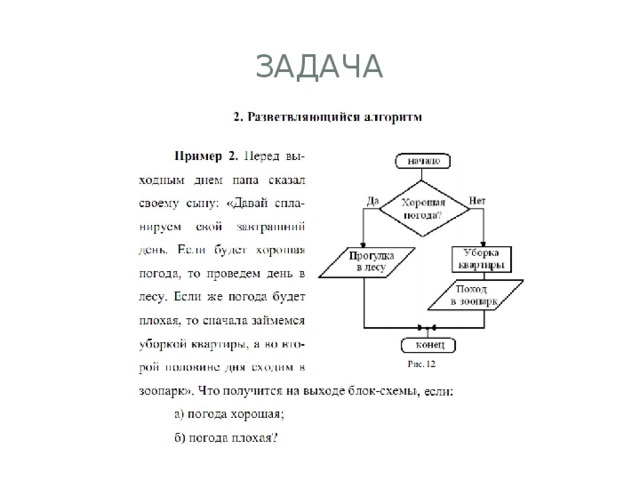
задача

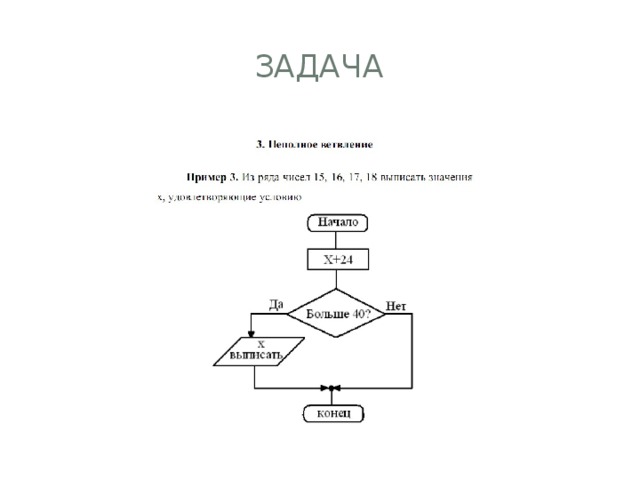
задача

задача

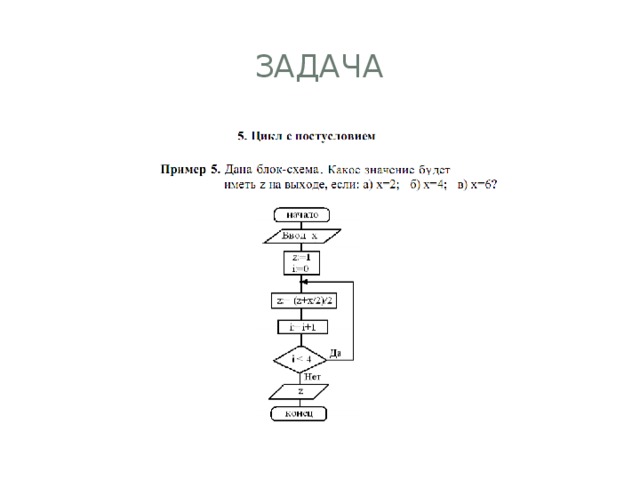
задача

Задачи

• Построить алгоритмы к следующим задачам:

• Даны три точки на плоскости, заданные своими координатами. Определить ближайшие из них.
• Дан ряд чисел a, b, c. Найти сумму отрицательных чисел.
• Даны x, y, z. Вычислить a и b, если a=(x-2)*y, b=(z+x)/y.