Факультативный курс
«Избранные вопросы математики»
Пояснительная записка
Программа курса «Избранные вопросы математики» рассчитана на 34 часа и может быть реализована в общеобразовательных 8-х классах и классах с углубленным изучением математики.
Основная задача обучения математике в школе заключается в обеспечении прочного и сознательного овладения учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому члену современного общества, достаточных для изучения смежных дисциплин и продолжения образования, а также в профессиональной деятельности, требующей достаточно высокой математической культуры.
Данный факультативный курс, строится на основе содержания программного учебного материала алгебраического компонента 8 класса. Он призван способствовать развитию умения рассуждать, доказывать, решать стандартные и нестандартные задачи, формированию познавательного интереса, формированию опыта творческой деятельности, развитию мышления и математических способностей учащихся.
Содержание и технология его усвоения направлены на формирование математической культуры школьников.
Формирование умения рассуждать, доказывать и решать задачи в процессе обучения математике является одной из важнейших педагогических задач. Содержание данного курса предоставляет большие возможности для решения данной задачи.
Алгебраические задачи являются хорошей основой для формирования умения рассуждать. Рассуждения при их выполнении являются, как правило, простыми, и это позволяет эффективно учить учащихся разбираться в структуре логического доказательства.
Решение алгебраических выражений является одним из важнейших элементов учебной деятельности школьника. Алгебраические задачи способствуют мотивации введения понятий, выявлению их свойств, усвоению терминологии и символики; раскрытию взаимосвязи одного понятия с другим. В процессе изучения теорем задачи выполняют такие функции, как выявление закономерностей, отраженных в теоремах; помогают усвоению содержания теоремы; раскрывают взаимосвязь изучаемой теоремы с другими теоремами.
В процессе проведения факультативных занятий следует продумать систему работы, направленную на формирование специальных умений и навыков по данному предмету, отвечающим таким требованиям, как правильность, осознанность, рациональность, обобщенность, автоматизм и прочность.
Важно в процессе работы продолжать формировать у учащихся способности к использованию основных эвристических приемов по поиску решений нестандартных задач.
Цель факультативного курса
- формирование умения рассуждать, доказывать и осуществлять поиск решений алгебраических задач на материале алгебраического компонента 8-ого класса;
- формирование опыта творческой деятельности;
- развитие уровня математического мышления и логического мышления, математических способностей и коммуникативных навыков у школьников.
Задачи факультативного курса
- систематизация, обобщение и углубление учебного материала, изученного на уроках математики 8 класса;
- развитие познавательного интереса школьников к изучению математики;
- формирование процессуальных черт их творческой деятельности;
- развитие логического мышления и интуиции учащихся;
- ознакомление учащихся с общими и частными эвристическими приемами поиска решения стандартных и нестандартных задач;
- расширение сфер ознакомления с нестандартными методами решения алгебраических задач.
Рекомендуемые формы и методы занятий
На занятиях при работе с определениями понятий, теоремами и их доказательствами, стандартными и нестандартными задачами могут использоваться фронтальная, самостоятельная и индивидуальная формы работы.
Важным средством углубления программного учебного материала является формирование математической культуры у школьников. Основными ее компонентами являются: положительная мотивация к математической деятельности; система полноценных знаний, умений и навыков; алгоритмическая, вычислительная, графическая, логическая культура; культура мышления и речи; культура поиска математических решений.
Методика работы на факультативных занятиях отличается от методики работы на уроке. Эти отличия заключаются в следующем:
- во-первых, особое внимание уделяется формированию приемов мыслительной деятельности (наблюдение и сравнение, обобщение и конкретизация, анализ и синтез, нахождение аналогий и их применение, построение гипотез и планирование действий и др.);
- во-вторых, большое место отводится общим и частным рассуждениям;
- в-третьих, систематически формируются умения применять эвристические приемы в различных сочетаниях;
- в-четвертых, постоянно осуществляется диалог учителя с учащимися при изучении теоретического материала и поиска способов решения любой предлагаемой задачи.
Содержание курса
Числа и вычисления. Решение задач по теме «Рациональные числа». Действительные числа и действиями над ними. Числовые закономерности и их использование при решении задач. Доказательство иррациональности чисел.
Выражения и их преобразования. Решение задач по теме «Арифметический квадратный корень». Решение задач повышенного уровня сложности по теме «Корень n-ой степени».
Методы разложения квадратного трехчлена на множители. Решение задач по теме «Квадратные уравнения. Теорема Виета». Задачи на исследование квадратных уравнений. Поиск закономерностей в процессе решения задач с помощью уравнений.
Решение задач по теме «Модуль действительного числа и его свойства».
Методы решения уравнений и неравенств, содержащих переменную под знаком модуля.
Решение задач по теме «Числовые неравенства и их свойства». Методы доказательств неравенств.
Уравнения и неравенства. Решение неравенств, сводящихся к линейным неравенствам. Системы и совокупности линейных неравенств с одной переменной. Методы решения уравнений и неравенств, содержащих переменную под знаком модуля.
Ожидаемые результаты
В результате изучения данного факультативного курса у учащихся будут сформированы прочные представления: о некоторых способах рассуждений и доказательств, о понятии «математическая задача», о различных способах решения задачи.
Учащиеся усовершенствуют такие способности деятельности, как:
- умения производить действия над действительными числами;
- умения выполнять тождественные преобразования выражений, содержащих квадратные корни;
- умения исследовать квадратные уравнения;
- умения решать уравнения, сводящиеся к квадратным уравнениям;
- умения решать уравнения и неравенства, содержащие переменную под знаком модуля;
- умения строить графики квадратных функций;
- умения решать текстовые задачи с помощью составления уравнений.
Изучение данного факультативного курса предполагает повышение уровня:
- познавательного интереса к математике;
- развитие логического мышления и математических способностей;
- получение опыта творческой деятельности;
- приобретение математической культуры;
- развитие способности учиться.
Тематический план
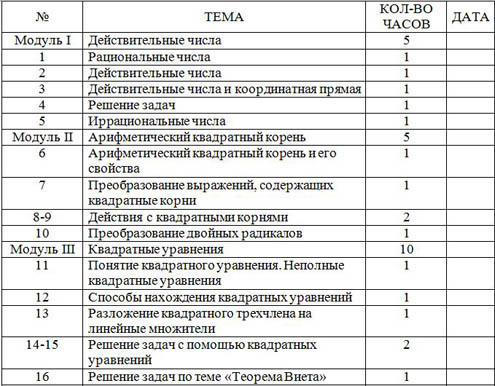
| № | ТЕМА | КОЛ-ВО ЧАСОВ | ДАТА |
| Модуль I | Действительные числа | 5 |
|
| 1 | Рациональные числа | 1 |
|
| 2 | Действительные числа | 1 |
|
| 3 | Действительные числа и координатная прямая | 1 |
|
| 4 | Решение задач | 1 |
|
| 5 | Иррациональные числа | 1 |
|
| Модуль II | Арифметический квадратный корень | 5 |
|
| 6 | Арифметический квадратный корень и его свойства | 1 |
|
| 7 | Преобразование выражений, содержащих квадратные корни | 1 |
|
| 8-9 | Действия с квадратными корнями | 2 |
|
| 10 | Преобразование двойных радикалов | 1 |
|
| Модуль III | Квадратные уравнения | 10 |
|
| 11 | Понятие квадратного уравнения. Неполные квадратные уравнения | 1 |
|
| 12 | Способы нахождения квадратных уравнений | 1 |
|
| 13 | Разложение квадратного трехчлена на линейные множители | 1 |
|
| 14-15 | Решение задач с помощью квадратных уравнений | 2 |
|
| 16 | Решение задач по теме «Теорема Виета» | 1 |
|
| 17 | Задачи на исследование знаков корней приведенного квадратного уравнения | 1 |
|
| 18 | Решение биквадратных уравнений | 1 |
|
| 19 | Решение уравнений, приводящихся к квадратным уравнениям | 1 |
|
| 20 | Задачи на нахождение целых корней многочлена с целыми коэффициентами |
|
|
| Модуль IV | Модуль числа | 8 |
|
| 21 | Модуль действительного числа | 1 |
|
| 22-23 | Метод промежутков при решении уравнений, содержащих переменную под знаком модуля | 2 |
|
| 24-25 | Решение уравнений | 2 |
|
| 26-27 | Метод промежутков при решении неравенств, содержащих переменную под знаком модуля | 2 |
|
| 28 | Решение неравенств | 1 |
|
| Модуль V | Числовые и линейные неравенства | 6 |
|
| 29 | Числовые неравенства и их свойства | 1 |
|
| 30 | Методы доказательства неравенств | 1 |
|
| 31 | Числовые промежутки | 1 |
|
| 32 | Задачи на исследование линейных неравенств | 1 |
|
| 33 | Решение неравенств, сводящихся к линейным неравенствам | 1 |
|
| 34 | Решение задач с использование неравенств | 1 |
|
Список литературы
Галицкий М.Л. и др. «Сборник задач по алгебре для 8-9 классов»; Учебное пособие для учащихся школ и классов с углубленным изучением курса математики: М., «Просвещение», 1992 г.
Березин В.Н. «Сборник задач для факультативных и внеклассных занятий по математике»; М., «Просвещение», 1980 г.
Фирсова Н.И. «Решение некоторых видов уравнений при помощи неравенств»; Математика в школе, 2002 г. №1
Дорофеев Г.В. «Как расположены корни трехчленов?»; «Квант», 1986 г. №7
Дорофеев Г.Ф. «Квадратный трехчлен в задачах»; Учебное пособие для учащихся: М., «Просвещение», 1994 г.
Туманов С.И. «Поиски решения задачи»; М., «Просвещение», 1980 г.
Шарыгин М.Ф. «Факультативный курс по математике. Решение задач»; М., «Просвещение», 1983 г.
Симонов А.Я., Бакаев Д.С. и др. «Система тренировочных задач и упражнений по математике»; М., «Просвещение», 1991 г.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Факультативный курс "Избранные вопросы математики" (83 КB)
Факультативный курс "Избранные вопросы математики" (83 КB)
 0
0 875
875 167
167 Нравится
0
Нравится
0


