Государственное учреждение образования
«Средняя школа №1 г. Осиповичи имени Б.М.Дмитриева»
Могилевской области
Факультативное занятие в 7 классе «Софизмы»
Автор: Лукьяненко Ирина Васильевна,
учитель математики 1 категории,
2020
Оглавление:
1.Введение……………………………………………………………………. 3
2.Основная часть……………………………………………………………...4
3.Литература…………………………………………………………………..8
4.Приложения…………………………………………………………………9
5. Слайды из SMART Notebook 11…………………………………………..
Введение
Исследовать софизмы действительно очень интересно и необычно. Порой сам попадаешься на уловки софиста, на столь безукоризненность его рассуждений. Перед тобой открывается какой-то особый мир рассуждений, которые поистине кажутся верными. Благодаря софизмам и парадоксам можно научится искать ошибки в рассуждениях других, научится грамотно строить свои рассуждения и логические объяснения. Если есть желание, то можно стать искусным софистом, добиться исключительного мастерства в искусстве красноречия или просто на досуге проверить свою смекалку. Факультативное занятие «Софизмы» в 7 классе развивает логическое мышление, помогает сознательному усвоению изучаемого материала, воспитывает вдумчивость, наблюдательность, критическое отношение к тому, что изучается. Кроме того, разбор софизмов увлекателен. Учащиеся с большим интересом будут воспринимать софизмы, чем труднее софизм, тем большее удовлетворение доставляет его разбор. Факультатив был разработан с применением интерактивной доски на программе SMART Notebook 11.
Цели и задачи занятия:
1.Образовательные:
способствовать расширению кругозора учащихся;
применение знаний и умений учащихся при моделировании практических ситуаций;
2.Развивающие
мотивация познавательной деятельности;
развитие у учащихся творческого мышления;
развитие самостоятельности при поиске, способствовать практическому применению умений и навыков, полученных на занятии;
создание условий для развития информационной, учебно-познавательной компетентности;
3.Воспитательные
формирование культуры умственного труда;
формирование научного мировоззрения;
воспитание умения работать в различных организационных формах.
Факультативное занятие «Софизмы»
Цели: Предполагается, что в ходе занятия, учащиеся смогут сформулировать определение софизма, познакомиться с различными видами софизмов, смогут понять, как найти ошибку в софизме.
Ход занятия:
1. Вводное слово учителя.
Здравствуйте ребята, здравствуйте уважаемые коллеги! У меня сегодня прекрасное настроение и надеюсь, что у присутствующих здесь ребят и гостей, через 45 минут оно только улучшиться. Сегодня мы поведем разговор об удивительных понятиях в математике, философии, логике, риторике, которые своими корнями уходит в далекую старину.
Я хочу вас спросить, вас когда-нибудь обманывали? Часто? А вот сегодня, я буду вас обманывать, вводить в заблуждение и пытаться заманить вас в ловушку. Попробуем?
2. Устная работа.
Таблица умножения (спросить учеников) Последний вопрос 2*2?
А я думаю, что 2*2=5 и сейчас это докажу.(Слайд 1,2)
Софизм «Дважды два пять» (демонстрируется на интерактивной доске)
Напишем тождество 4:4=5:5.
Вынесем из каждой части тождества общие множители за скобки, получаем: 4(1:1) = 5(1:1) или (2·2)·(1:1) = 5·(1:1)
Так как 1:1 = 1, то сократим и получим 2 · 2 = 5. Верно? Нет? Тогда где же ошибка? (Выслушать ответы учеников)
Ошибка сделана при вынесении общих множителей 4 из левой части и 5 из правой. Действительно, 4:4 = 1:1, но 4:4 ≠ 4(1:1). Так выносить за скобки нельзя!
Учитель: В математике существует такое понятие как софизм - это умышленно ложное утверждение, которое имеет видимость правильного и ошибка искусно замаскирована.
3. Тема нашего занятия: «Софизмы»
Софизм (от греч. sophisma – уловка, выдумка, головоломка, ухищрение, выдумка) — ложное умозаключение, которое, тем не менее, при поверхностном рассмотрении кажется правильным. (Слайд 3)
Ребята, а как вы думаете, чем мы сегодня будем заниматься? (выслушать ответы учащихся)
В ходе сегодняшнего занятия мне бы хотелось, чтобы вы познакомились с различными видами софизмов, смогли понять, как найти ошибку в софизме и смогли дать свое определение софизма. (Слайд4)
А сейчас внимание на доску, я вам предлагаю познакомиться с арифметическим софизмом.
4. Алгебраический софизм (работаем в парах при обсуждении, поиске ответа) (Слайд 5)
Докажем, что 5 = 6. С этой целью возьмем числовое тождество:
35 + 10 – 45 = 42 + 12 – 54
Вынесем общие множители левой и правой частей за скобки. Получим:
5 * (7 + 2 – 9) = 6 * (7 + 2 – 9)
Разделим обе части этого равенства на общий множитель, заключенный в скобки. Получим 5=6. В чем ошибка?
Ответ: 7 + 2 – 9 = 0, а на 0 делить нельзя!
На партах у вас есть подсказки, как находить ошибки в софизме. Давайте их зачитаем. (Приложение 1)(Слайд 6)
5. Практическое задание «Трубочки и ножницы» (Слайд 7)
Два раза по два (т.е. дважды два) будет не четыре, а три.
Возьмем трубочку и разрежем ее пополам. Это один раз два. Затем возьмем одну из половинок и разрежем ее пополам. Это второй раз два. В результате получилось три части исходной трубочки. Таким образом, два раза по два будет не четыре, а три.
Ответ: В этом рассуждении, так же, как и в предыдущем, смешиваются различные вещи, отождествляется нетождественное: операция умножения на два и операция деления на два – одно неявно подменяется другим, в результате чего достигается эффект внешней правильности и убедительности предложенного «доказательства».
6. Физкультминутка «Веселые частушки» (Слайд 8,9)
Улыбнитесь, как кот. Покажите, как хмурится облако, подсолнух тянется к солнышку.
А теперь все вместе пропоем математические частушки.
1)117, 117,
19, 9, 5!
117, 117,
48, 35!
2)2,15,42,
42,15,
37, 08, 5,
20, 20,20!
3) 7, 14, 105,
2, 00, 13,
37, 08, 5,
20,20,20!
7.Работа по группам. (Слайд10)
1 группа. Один рубль не равен ста копейкам.
Известно, что любые два равенства можно перемножить почленно, не нарушая при этом равенства, т. е. если, а = b и c = d, то ac = bd. Применим это положение к двум очевидным равенствам: 1 рубль = 100 копейкам, 10 рублей = 1000 копеек. Перемножая эти равенства почленно, получим: 10 рублей = 100 000 копеек и, наконец, разделив последнее равенство на 10, получим, что 1 рубль = 10 000 копеек.
Таким образом, один рубль не равен ста копейкам.
Разбор софизма. Ошибка, допущенная в этом софизме, состоит в нарушении правила действий с именованными величинами: все действия, совершаемые над величинами, необходимо совершать также и над их размерностями.
2 группа. Логический софизм.
Что ты не терял, то имеешь. Рога ты не терял. Значит, у тебя рога есть.
Ответ: Если у тебя нет рогов, ты не сможешь их потерять.
8.Геометрический софизм. (Приложение 2)(слайд11)
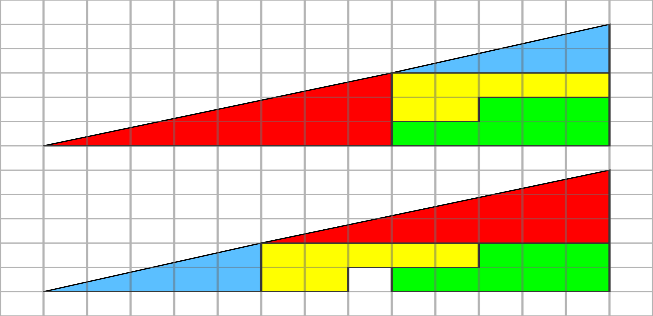
Если начертить на листке бумаги в клетку фигуру, названную «треугольником Керри» в честь её первооткрывателя, и разрезать её вдоль прямых, то переставив части фигуры, изображенную на рис. 2, мы обнаружим, что внизу новой фигуры появилась дырка площадью в 1клетки. Иначе говоря, суммарная площадь частей исходной фигуры при переставлении уменьшилась. Куда исчезла клетка?
9. Заключение. Подведение итогов.
Ребята, а давайте вернемся к началу нашего занятия. Чем мы предполагали заняться? И получилось ли? (выслушать ответы учащихся)
(слайд12, 13)
10. Домашнее задание.
(слайд 14)
1. Составить софизм 2=3
2 .Их было десять чудаков,
Тех путников усталых,
Что в дверь решились постучать
Таверны «Славный малый».
— Пусти, хозяин, ночевать,
Не будешь ты в убытке,
Нам только ночку переспать,
Промокли мы до нитки.
Хозяин тем гостям был рад,
Да вот беда некстати:
Лишь девять комнат у него
И девять лишь кроватей.
Восьми гостям я предложу
Постели честь по чести, -
А двум придется ночь проспать
В одной кровати вместе.
Лишь он сказал, и сразу крик,
От гнева красны лица:
Никто из всех десятерых
Не хочет потесниться.
Как охладить страстей тех пыл,
Умерить те волненья?
Но старый плут хозяин был
И разрешил сомненья.
Двух первых путников пока,
Чтоб не судили строго,
Просил пройти он в номер «А»
И подождать немного.
Спал третий в «Б», четвертый в «В»,
В «Г» спал всю ночь наш пятый,
В «Д», «Е», «Ж», «3» нашли ночлег
С шестого по девятый.
Потом, вернувшись снова в «А»,
Где ждали его двое,
Он ключ от «И» вручить был рад
Десятому герою.
Хоть много лет с тех пор прошло,
Неясно никому,
Как смог хозяин разместить
Гостей по одному.
Иль арифметика стара,
Иль чудо перед нами.
Понять, что, как и почему,
Вы постарайтесь сами…
11. Рефлексия. Продолжите фразу:
Сегодня я… узнал, было трудно…я научился…(слайд 15)
12. Заключительное слово учителя: Самым известным софистом был Зенон из города Ален. До нас дошли 4 его софизма. В одном Зенон утверждает, что для того, чтобы пройти какой-нибудь путь, нужно непременно миновать его середину. Само по себе рассуждение верное. Но далее Зенон рассуждает так: если мы дошли до середины пути, то нам остаётся ещё полпути, у которого тоже есть своя середина. И так без конца. Сколько бы мы ни шли вперед, всегда остается какая-то не пройденная часть пути, у которой есть своя середина. Ну, а я, желаю вам двигаться только вперед, несмотря на трудности, ожидающие вас впереди! Спасибо за работу!
Литература:
1. «Математические софизмы». Книга для учащихся 7-11 классов. Авторы: А.Г. Мадера, Д.А. Мадера. Москва «Просвещение» 2003.
2.«Математическая шкатулка». Автор: Ф.Ф. Нагибин. Государственное учебно-педагогическое издательство министерства просвещения РСФСР 1961.
3.«Математика после уроков». Пособие для учителей. Авторы: М.Б.Балк, Г.Д.Балк. Москва «Просвещение», 1971.5. Обреимов В.И., «Математические софизмы», СПб, 1989;
Приложение 1
Способ нахождения ошибки в софизме
1.Внимательно прочитать условие предложенной вам задачи.
2.Выясните, соблюдены ли все условия применимости теорем, правил, формул, соблюдена ли логичность.
3.Проверяйте результаты преобразования обратным действием.
Приложение 2
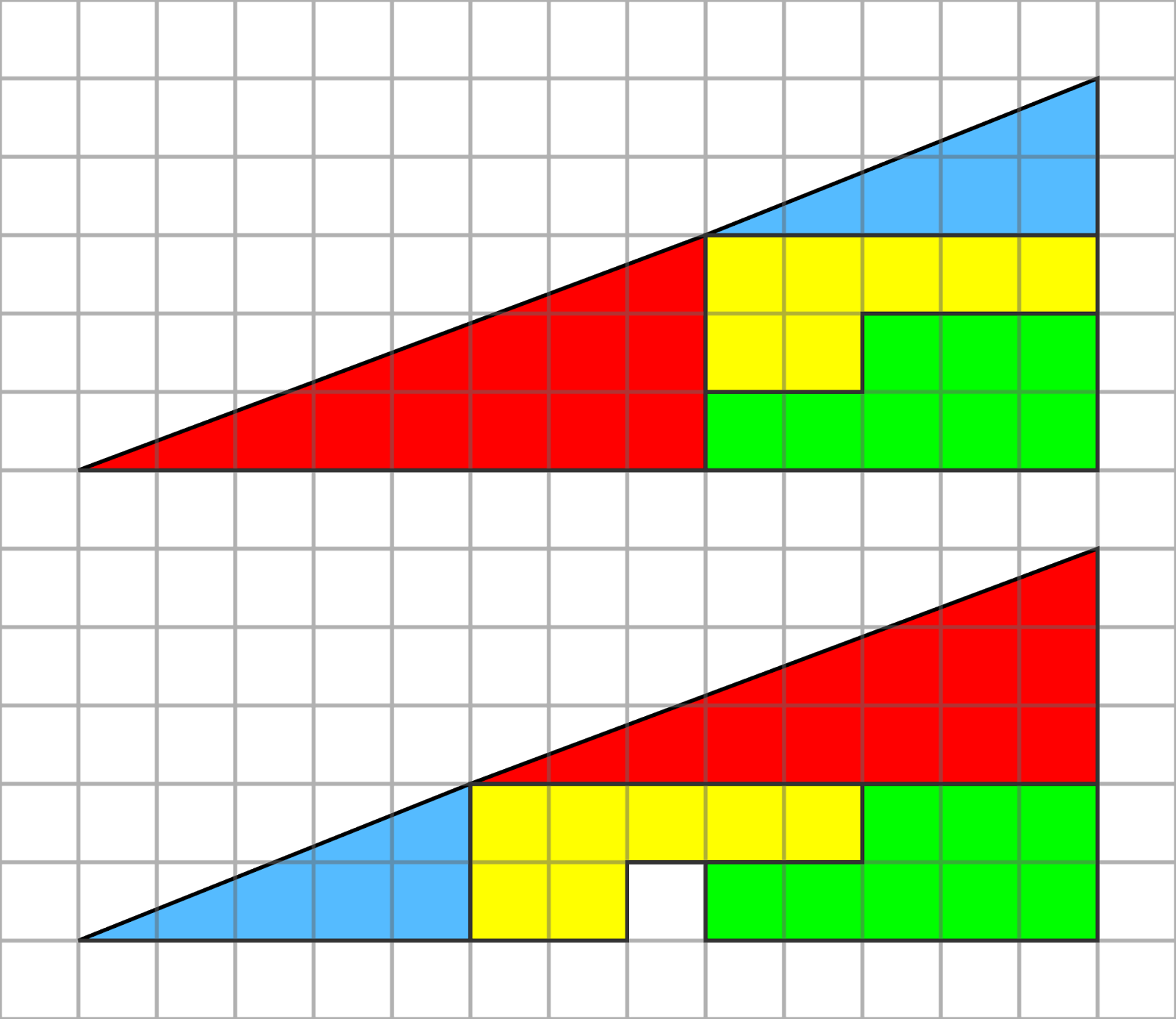
11

 Получите свидетельство
Получите свидетельство Вход
Вход











 Факультативное занятие "Софизмы" (125.75 KB)
Факультативное занятие "Софизмы" (125.75 KB)
 0
0 421
421 21
21 Нравится
0
Нравится
0


