Получите свидетельство
Вход
Элективный курс «Подготовка к ОГЭ»
Автор: учитель первой категории
Кочевых Р. П.
0, b 2) k 3) k 0 4) k 0, b 0 А Б В 1 3 2 " width="640"
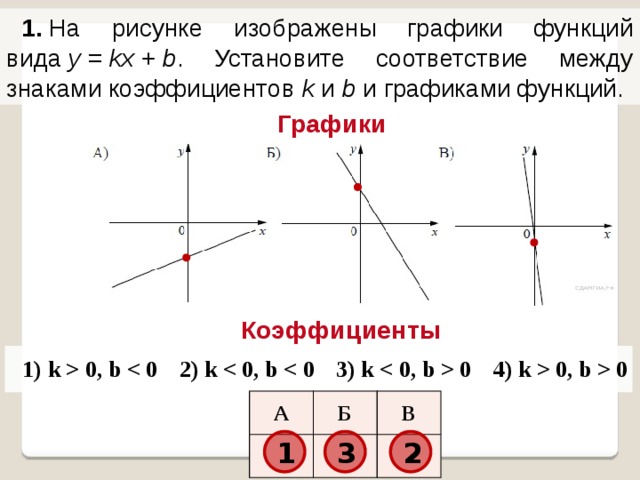
1. На рисунке изображены графики функций вида y = kx + b . Установите соответствие между знаками коэффициентов k и b и графиками функций.
Графики
Коэффициенты
1) k 0, b
2) k
3) k 0
4) k 0, b 0
А
Б
В
1
3
2
0, b 0 В) k 0, b А Б В 3 2 1 " width="640"
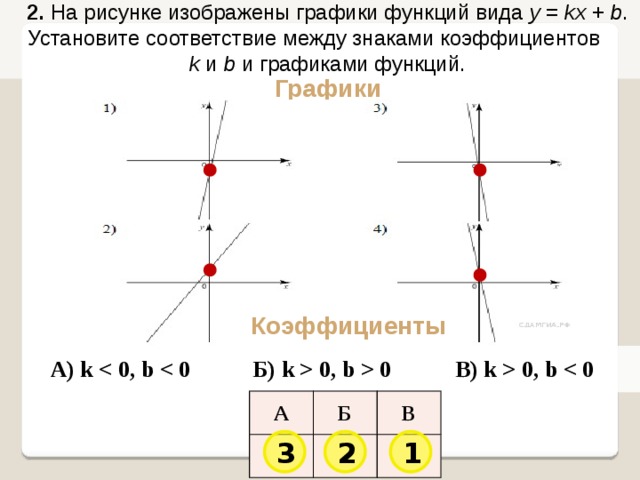
2. На рисунке изображены графики функций вида y = kx + b . Установите соответствие между знаками коэффициентов
k и b и графиками функций.
Графики
Коэффициенты
А) k
Б) k 0, b 0
В) k 0, b
А
Б
В
3
2
1
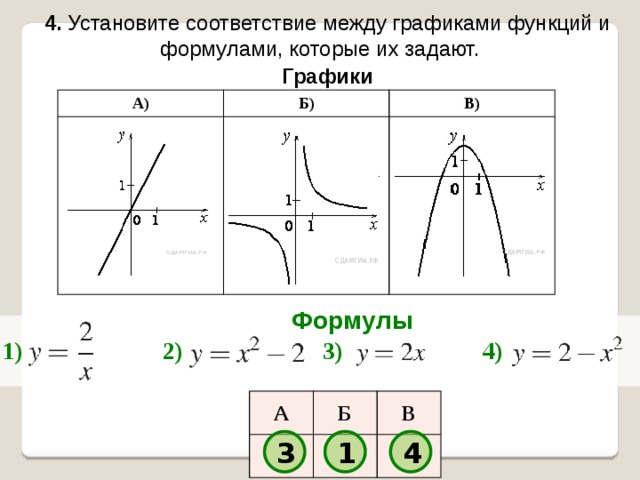
4. Установите соответствие между графиками функций и формулами, которые их задают.
Графики
А)
Б)
В)
Формулы
1)
2)
3)
4)
А
Б
В
3
1
4
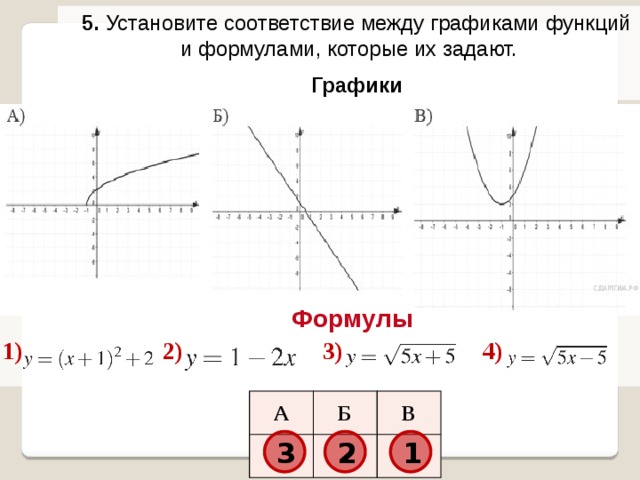
5. Установите соответствие между графиками функций и формулами, которые их задают.
Графики
Формулы
1)
2)
3)
4)
А
Б
В
3
2
1
0 при −1x " width="640"
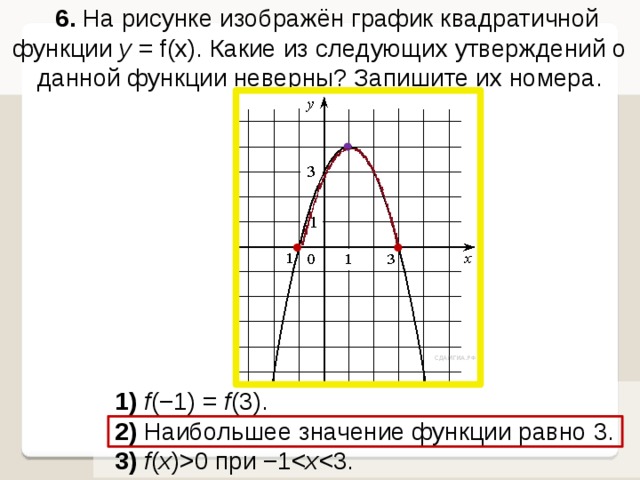
6. На рисунке изображён график квадратичной функции y = f(x). Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f (−1) = f (3).
2) Наибольшее значение функции равно 3.
3) f ( x )0 при −1x
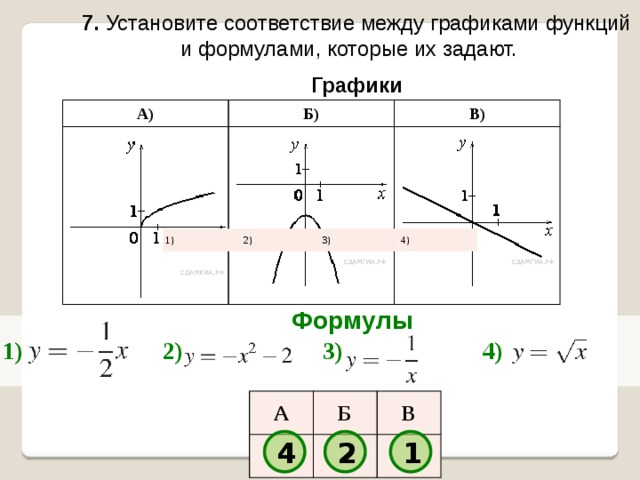
7. Установите соответствие между графиками функций и формулами, которые их задают.
Графики
А)
Б)
В)
1)
2)
3)
4)
Формулы
1)
2)
3)
4)
А
Б
В
1
2
4
![8. На рисунке изображён график функции y = ax 2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру. УТВЕРЖДЕНИЯ А) функция возрастает на промежутке ПРОМЕЖУТКИ Б) функция убывает на промежутке 1) [1;2] 2) [0;2] 3) [-1;0] 4) [-2;3] А Б 3 1](https://fsd.videouroki.net/html/2018/02/10/v_5a7ed91b338ef/img7.jpg)
8. На рисунке изображён график функции y = ax 2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
УТВЕРЖДЕНИЯ
А) функция возрастает на промежутке
ПРОМЕЖУТКИ
Б) функция убывает на промежутке
1) [1;2] 2) [0;2]
3) [-1;0] 4) [-2;3]
А
Б
3
1
0, c 2) a 0 3) a 0, c 0 4) a А Б В Г 4 1 2 3 " width="640"
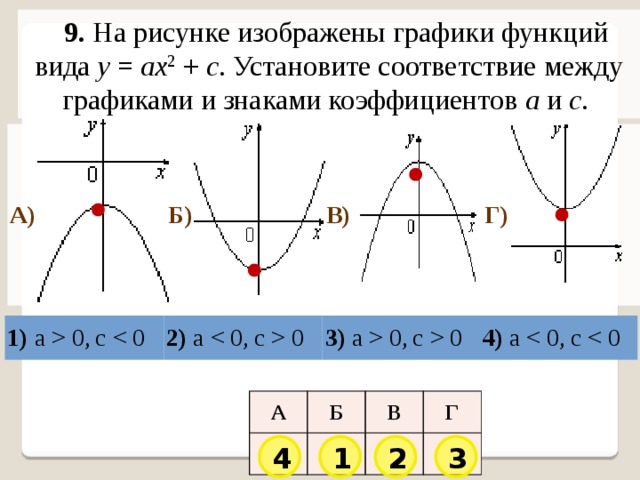
9. На рисунке изображены графики функций вида y = ax 2 + c . Установите соответствие между графиками и знаками коэффициентов a и c .
А)
Б)
В)
Г)
1) a 0, c
2) a 0
3) a 0, c 0
4) a
А
Б
В
Г
4
1
2
3
0, b 0 3) k 0, b 4) k 0 А Б В 2 1 4 " width="640"
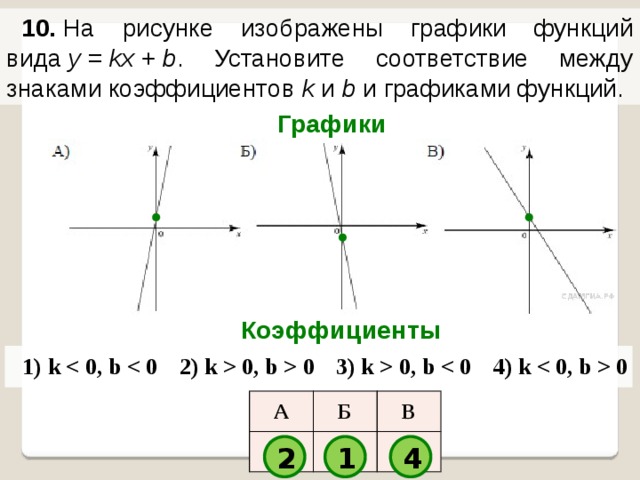
10. На рисунке изображены графики функций вида y = kx + b . Установите соответствие между знаками коэффициентов k и b и графиками функций.
Графики
Коэффициенты
1) k
2) k 0, b 0
3) k 0, b
4) k 0
А
Б
В
2
1
4
Модуль «Геометрия»
Подготовка к ОГЭ
19. Какие из следующих утверждений верны?
1) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.
2) Любые два равнобедренных треугольника подобны.
3) Любые два прямоугольных треугольника подобны.
4) Треугольник ABC , у которого AB = 3, BC = 4, AC = 5, является тупоугольным.
24. Какие из следующих утверждений верны?
1) Площадь многоугольника, описанного около окружности, равна произведению его периметра на радиус вписанной окружности.
2) Если диагонали ромба равна 3 и 4, то его площадь равна 6.
3) Площадь трапеции меньше произведения суммы оснований на высоту.
4) Площадь прямоугольного треугольника меньше произведения его катетов.
23. Какие из следующих утверждений верны?
1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.
2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
3) Треугольник ABC , у которого AB = 5, BC = 6, AC = 7, является остроугольным.
4) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
21. Какие из следующих утверждений верны?
1) Сумма углов выпуклого четырехугольника равна 180°.
2) Если один из углов параллелограмма равен 60°, то противоположный ему угол равен 120°.
3) Диагонали квадрата делят его углы пополам.
4) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.
22. Какие из следующих утверждений верны?
1) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
2) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
3) Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°.
4) Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
20. Какое из следующих утверждений верно?
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Диагонали ромба равны.
3) Тангенс любого острого угла меньше единицы.
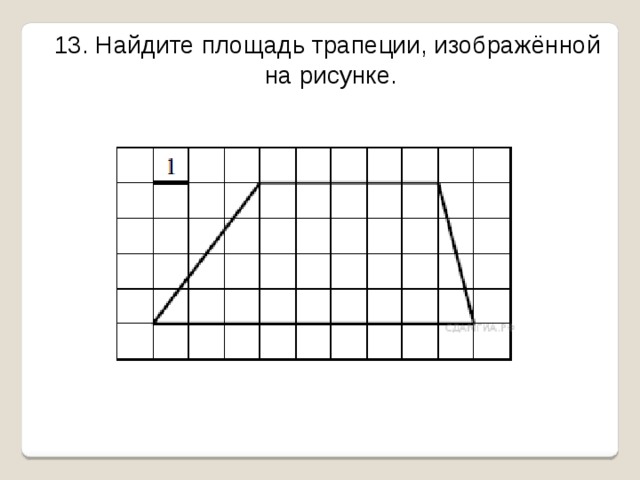
13. Найдите площадь трапеции, изображённой
на рисунке.
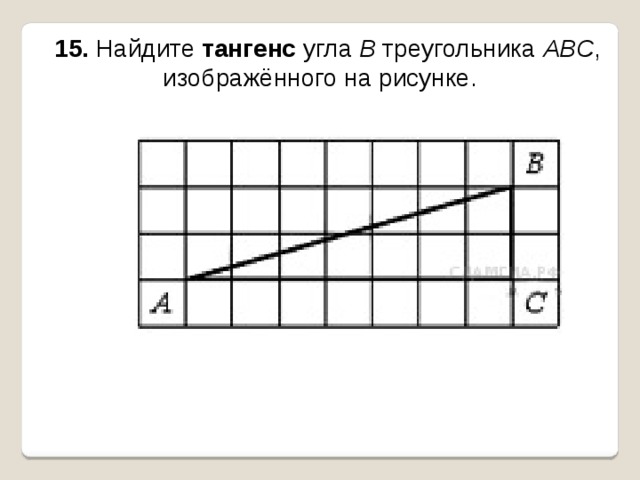
15. Найдите тангенс угла В треугольника ABC , изображённого на рисунке.
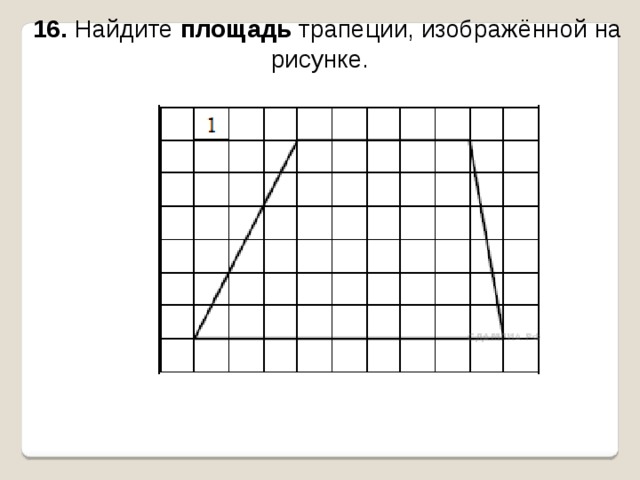
16. Найдите площадь трапеции, изображённой на рисунке.
Элективный курс "Подготовка к ОГЭ" (281.8 KB)
0
954
23
Нравится
0
