Муниципальное бюджетное образовательное учреждение средняя
общеобразовательная школа с углубленным изучением отдельных
предметов № 24г. Волжского Волгоградской области
( МБОУ СОШ с углубленным изучением отдельных предметов №24)
МБОУ СОШ с углубленным изучением отдельных предметов №24)
ОКПО 48045526; ОГРН 1023402001952 ИНН/КПП 3435881053/ 343501001 404121 Волгоградская обл., г.Волжский,
ул.Пушкина,64, тел/факс (8443) 38-36-92; E-mail: shkla24.71 @ mail.ru/ shkla24 @ rambler.ru
УТВЕРЖДАЮ
Директор МБОУ СОШ № 24_
О.А. Баранова
ЭЛЕКТИВНЫЙ КУРС
Подготовка к ЕГЭ
название элективного курса
для обучающихся 11 классов
Количество часов 50
Рассмотрено
на заседании методического совета
МБОУ СОШ №24
Протокол №
от « » 20 г.
Разработчик программы:
учитель математики
МБОУ СОШ №24
Н.В. Мирецкая
Пояснительная записка
Программа элективного курса «Подготовка к ЕГЭ» предназначена для учащихся 11 класса с профильным изучением математики и рассчитана на 50 часов.
Математика- предмет, изучающийся с первого по выпускной класс. Объем содержательных единиц, которые должен знать старшеклассник по математике, чрезвычайно велик. Предлагаемый курс является развитием системы ранее приобретённых знаний, и его цель - углубить теоретический багаж выпускника и сформировать у него прочные навыки применения этих знаний, как в стандартных, так и в изменённых ситуациях. Данный курс позволит учащимся повторить и систематизировать большое количество материала, необходимое для успешной сдачи экзамена.
Целью данного курса является расширение и углубление знаний и умений учащихся для успешной сдачи ЕГЭ.
Задачи:
развитие логического мышления, пространственного воображения, критичности мышления на уровне, необходимом для обучения в высшей школе;
формирование умений применять знания в изменённых ситуациях.
В процессе обучения учащиеся приобретают следующие умения:
решать текстовые задачи
решать тригонометрические, логарифмические, иррациональные, показательные уравнения и неравенства, системы уравнений;
решать уравнения содержащие модуль, параметры, комбинированные уравнения
решать геометрические задачи на комбинацию тел;
решать задания повышенного уровня;
В ходе изучения курса учащиеся овладевают разнообразными способами деятельности, приобретают и совершенствуют опыт самостоятельной работы с источниками информации, обобщения и систематизации.
Организация и проведение аттестации учащихся
Изучение курса предполагается построить в основном в виде уроков – практикумов, на которых можно работать как со всем классом, так и с группами учащихся.
Чтобы оценить динамику усвоения учащимися того или иного раздела будут проведены промежуточные и итоговая аттестации по данному разделу. Промежуточная аттестация по каждому из разделов будет проведена в виде домашних самостоятельных работ. Эта форма контроля выбрана потому что дома ученик не ограничен во времени, а значит может решить большее количество заданий .
Итоговая контрольная работа проводится в формате ЕГЭ
Содержание изучаемого курса.
1.Решение текстовых задач 5ч
Задачи на проценты, смеси и сплавы, движение, работу.
Арифметическая и геометрическая прогрессии.
Цель: Повторить теоретический материал (проценты, пропорции). Повторить методику решения задач на движение, работу, сплавы и смеси. Прогрессии.
2. Выражения и преобразования 5ч.
Тождественные преобразование иррациональных выражений
Степень с рациональным показателем.
Синус, косинус, тангенс, котангенс.
Логарифмы.
Цель: Повторить свойства степени, логарифма, корней п-й степени, свойства синуса, косинуса, тангенса, котангенса.
3. Уравнения и неравенства 11ч.
Общие приемы решения уравнений.
Решение тригонометрических, иррациональных, логарифмических, показательных уравнений, неравенств и систем уравнений. Решение комбинированных уравнений. Решение уравнений содержащих модуль. Отбор корней уравнения.
Цель: рассмотреть основные приемы решения различных уравнений, неравенств и систем уравнений. Классифицировать их, рассмотреть решение комбинированных уравнений.
4. Функции 6ч.
Числовые функции и их свойства. Область определения (значения) сложных функций. Производная ее применение. Первообразная. Площадь криволинейной трапеции.
Цель: рассмотреть различные виды функций их свойства. Область определения, область значения функции. Применение производной. Первообразная, площадь криволинейной трапеции
5. Геометрические фигуры и их свойства 5ч.
Решение задач планиметрии.
Решение задач на комбинацию тел.
Цель: рассмотреть различные задачи планиметрии, задачи стереометрии на комбинацию тел.
6. Решение вариантов ЕГЭ -12ч
7. Пробный ЕГЭ – 6 час.
Тематическое планирование
|
| Тема занятия | Кол-во часов |
|
|
| Решение задач (5ч) |
|
|
| 1 | Решение задач на проценты | 1 | Урок-практикум |
| 2 | Решение задач на смеси и сплавы | 1 | Урок-практикум |
| 3 | Решение задач на прогрессии | 1 | Урок-практикум |
| 4 | Решение задач на движение | 1 | Урок-практикум |
| 5 | Решение задач на работу | 1 | Урок-практикум |
|
|
|
|
|
|
| Выражения и преобразования (5ч) |
|
|
| 6 | Степень с целым показателем | 1 | Урок-практикум |
| 7 | Степень с рациональным показателем й | 1 | Урок-практикум |
| 8 | Тождественные преобразование иррациональных выражений |
|
|
| 9 | Преобразование тригонометрических выражений | 1 | Урок-практикум |
| 10 | Логарифмы. Свойства логарифмов | 1 | Урок-практикум |
|
| Уравнения и неравенства (11ч) |
|
|
| 11 | Решение тригонометрических уравнений и систем уравнений. | 1 | Урок-практикум |
| 12 | Решение тригонометрических уравнений и неравенств | 1 | Групповая работа |
| 13 | Отбор корней тригонометрических уравнений различными способами. |
| Урок-практикум |
| 14 | Решение иррациональных уравнений и систем уравнений, неравенств | 1 | Урок-практикум |
| 15 | Решение логарифмических уравнений и систем уравнений | 1 | Групповая работа |
| 16 | Решение показательных уравнений и систем уравнений, неравенств | 1 | Урок-практикум |
| 17 | Решение уравнений содержащих модуль. | 1 | Урок-практикум |
| 18 | Решение уравнений содержащих модуль. |
| Урок-практикум |
| 19 | Решение комбинированных уравнений, неравенств | 1 | Урок-лекция |
| 20 | Решение комбинированных уравнений, неравенств | 1 | Урок-практикум |
| 21 | Решение систем уравнений. | 1 |
|
|
| Функции (6ч) |
|
|
| 22 | Числовые функции и их свойства. | 1 | Урок-практикум |
| 23 | Нахождение области определения (значения) сложных функций. | 1 | Урок-практикум |
| 24 | Наибольшее и наименьшее значения функций. | 1 | Урок-практикум |
| 25 | Производная. Геометрический и физический смысл производной. |
|
|
| 26 | Производная ее применение | 1 | Урок-практикум |
| 27 | Первообразная. Площадь криволинейной трапеции.. | 1 | Урок-практикум |
|
| Геометрические фигуры и их свойства(5ч) |
|
|
| 28 | Решение задач планиметрии. | 1 | Урок-лекция |
| 29 | Решение задач планиметрии. | 1 | Урок-практикум |
| 30 | Решение задач планиметрии. | 1 | Урок-практикум |
| 31 | Решение задач на комбинацию тел. | 1 | Урок-практикум |
| 32 | Решение задач на комбинацию тел. | 1 | Урок-практикум |
| 33-44 | Решение вариантов ЕГЭ (12ч.) | 12 |
|
| 45-50 | Пробный ЕГЭ | 6 |
|
Список рекомендуемой литературы для учителя и ученика
6.Открытый банк заданий ЕГЭ по математике http://mathege.ru
Приложение
ПРИМЕРНЫЕ САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
К ЭЛЕКТИВНОМУ КУРСУ
«ПОДГОТОВКА К ЕДИНОМУ ГОСУДАРСТВЕННОМУ ЭКЗАМЕНУ»
Домашняя самостоятельная работа №1 по теме
«Решение задач»
1. .Решить задачу
При каком значении n длины сторон n-угольника могут образовывать геометрическую прогрессию со знаменателем q=1,9?
2. Двум рабочим было поручено изготовить партию деталей . Первый рабочий работал в понедельник, среду, пятницу и изготовил 133 детали. Второй работал во вторник и четверг и изготовил 78 деталей. По окончанию работ было замечено, что, начиная со вторника каждый день изготавливалось деталей на один и тот же процент больше, чем в предыдущий. Сколько деталей изготовили в пятницу?
3.500 кг железной руды содержали 30% железа. После удаления некоторого количества примесей содержание железа в руде увеличилось до 50%. Какое количество примесей (в кг ) было удалено из руды.
4. Два спиртовых раствора борной кислоты одинаковой массы слили в один сосуд. Скольки процентный раствор получили в результате, если первый раствор был пятипроцентный (5% кислоты и 95%спирта), а второй однопроцентный.
5.Проехав 120км, что составляло половину всего пути, пассажир лег спать и проспал до тех пор, пока не осталось ехать половину того пути который он проехал спящим. Сколько километров пути пассажир проехал спящим?
Контрольная работа № 1 по теме
«Решение задач»
| Вариант 1 | Вариант 2 |
| 1Решить задачу Если к четырем числам a,b,c,d, составляющим геометрическую прогрессию, прибавить соответственно 4,21,29, и 1, то получится 4 числа, составляющие арифметическую прогрессию. Найдите сумму чисел a, b, c, d. | 1.Решить задачу Если к трем числам a,b,c, составляющим геометрическую прогрессию со знаменателем 3, прибавить соответственно 13,28 и 15, то получится 4 числа, составляющие арифметическую прогрессию. Найдите сумму чисел a, b, c. |
| 2.Решить задачу Начальный капитал акционерного общества составляет 16 миллионов рублей. Ежегодно капитал увеличивается на 50%. Через сколько лет капитал акционерного общества превысит 211 миллионов рублей?
| 2.Решить задачу Известно, что 19 февраля длина световой части дня составила 10 часов. Через сколько суток она увеличится на 6%, если каждый день к световой части суток добавляется 4,5 минуты?
|
Домашняя самостоятельная работа №2 по теме
«Выражения и преобразования»
1.Найти значение выражения 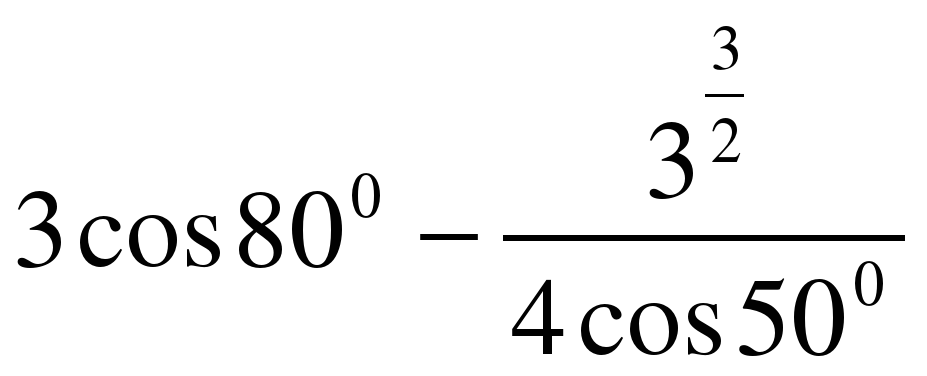 .
.
2.Вычислить ![]() .
.
3. Вычислить а)![]() б)
б)![]() .
.
4 Вычислить ![]() , если
, если ![]()
.5.Упростить![]() .
.
6.Сравните числа ![]() и
и ![]() .
.
Контрольная работа № 2 по теме
«Выражения и преобразования»
| Вариант 1 | Вариант 2 |
| 1.Сократите дробь
| 1.Сократите дробь
|
| 2.Найти значение выражения | 2.Представьте в виде произведения cos3x+sin2xsinx |
| 3.Найти значение выражения
| 3.Найти значение выражения
|
Домашняя самостоятельная работа №3 по теме
«Решение уравнений»
1.Решите уравнение 4cosxctgx+4ctgx+sinx.
2.Решите уравнение ![]() .
.
3.Найдите число целых решений уравнения ![]() .
.
4. Решить неравенство а)![]() б)
б) ![]() .
.
5. Найти сумму решений уравнения ![]()
6.Решите уравнение:![]()
Контрольная работа № 3 по теме
«Решение уравнений»
| Вариант 1 | Вариант 2 |
| 1.Найдите сумму корней уравнения:
| 1.Найдите сумму корней уравнения:
|
| 2.Решите систему уравнений: | 2.Решите систему уравнений: |
| 3.Решите уравнение:
| 3.Решите уравнение:
|
Домашняя самостоятельная работа №4 по теме
«Решение уравнений и неравенств содержащих модуль, комбинированных уравнений »
1.Решите уравнение:
2.Найдите количество действительных корней уравнения:
3.Найдите количество натуральных решений неравенства:
4. Найдите сумму квадратов целых решений неравенства:
5.Найдите среднее арифметическое корней уравнения принадлежащих отрезку -2;2.
6.Найдите все значения р, ![]() при которых уравнение имеет хотя бы один корень.
при которых уравнение имеет хотя бы один корень.
Контрольная работа №4 по теме
«Решение уравнений и неравенств содержащих модуль, комбинированных уравнений »
| Вариант 1 | Вариант 2 |
| 1.Найти сумму корней уравнения: | 1.Найти сумму корней уравнения: |
| 2.Найдите наименьшее натуральное число, являющееся решением неравенства : . | 2.Найдите наименьшее натуральное число, являющееся решением неравенства : . |
| 3. Решите уравнение | 3. Решите уравнение :
|
Домашняя самостоятельная работа №5 по теме
«Функции»![]()
1.Найдите наибольшее значение функции:
2.Найдите произведение всех целых чисел, входящих в область определения функции
3. Найдите площадь фигуры, ограниченной линиями у=4-х², у=0,
4. Найдите множество значений функции:
5.Найдите наименьшее целое t, при котором функция не имеет экстремумов.
Контрольная работа №5 по теме
«Функции»
| Вариант 1 | Вариант 2 |
| 1.Найдите максимум функции: | 1.Найдите максимум функции |
| 2.Найдите наименьшее значение функции: | 2.Найдите наименьшее значение функции: |
| 3. Вычислите площадь фигуры, ограниченной линиями у=1,25х³, у=0, х=0,4. | 3.Вычислить площадь фигуры, ограниченной линиями у=27х², у=0, х=2. |
Домашняя самостоятельная работа №6 по теме
«Геометрические фигуры и их свойства»![]()
1.В равнобедренном треугольнике KLM с основанием KM высоты LP и KB пересекаются в точкеO. Найдите площадь треугольникаKLO, если LO=5, PO=4.
2.В конус, осевое сечение которого - равносторонний треугольник, вписан шар. Найти объем конуса, если объем шара равен 8.
3. Основанием прямой призмы служит равнобедренная трапеция АВСД, в которой АВ=СД=13, ВС=11, АД=21. Площадь диагонального сечения призмы равна 180. Найдите площадь полной поверхности призмы
Контрольная работа №6 по теме
«Геометрические фигуры и их свойства»![]()
| Вариант 1 | Вариант 2 |
| 1 Середина высоты находится на расстоянииот ближайших сторон равностороннего треугольника. Найдите периметр этого треугольника.
| 1.Точка, расположенная внутри равнобедренного треугольника, с углом при основании 30º, находится на одинаковом расстоянии от боковых сторон и на расстоянии10 от основания. Найдите длину боковой стороны треугольника. |
| 2.В основании прямой призмы лежит прямоугольный треугольник АВС. Радиус описанной около него окружности равен 6, катет АС стягивает дугу, равную 60º.Через диагональ боковой грани, проходящей через другой катет ВС, проведена плоскость, перпендикулярная этой грани и образующая с плоскостью основания угол 30º. Определите площадь сечения. | 2. В основании прямой призмы лежит прямоугольный треугольник АВС. Катет ВС стягивает дугу, равную 60º.Через диагональ боковой грани, проходящей через другой катет АС, проведена плоскость, перпендикулярная этой грани и образующая с плоскостью основания угол 30º. Определите радиус описанной около треугольника АВС окружности, если площадь сечения равна 16. |

 Получите свидетельство
Получите свидетельство Вход
Вход













 Элективный курс "Подготовка к ЕГЭ по математике" (221 KB)
Элективный курс "Подготовка к ЕГЭ по математике" (221 KB)
 0
0 1361
1361 251
251 Нравится
0
Нравится
0


