Экономические задачи в ЕГЭ

Экономические задачи в ЕГЭ

Гнатюк И.И.

• Большинство задач, включенных в учебники математики по разным программам, являются задачами с экономическим содержанием.
• Школьная математика должна включать в себя обе ветви современной математики (теоретическую и прикладную). Под прикладной обычно понимается тот раздел математики, в котором демонстрируется применение математической теории в практических ситуациях. В школьном курсе математики при решении прикладных задач естественным этапом является математическое моделирование реальных процессов.

Вкладчик положил в банк 30000 рублей.Банк начисляет ежегодно 8% дохода на сумму вклада, находящуюся на счете вкладчика в начале года. Какая сумма будет на счете через два года?

Задача на «Сложные проценты» по программе 8 класса

После двух последних снижений цен на одно и то же число процентов цена одной упаковки лекарства снизилась с 300 рублей до192руб.На сколько процентов снижалась цена одной упаковки лекарства каждый раз?

Задача 9 класс

В конце года банк начисляет 4% к сумме вклада.Какую сумму получит вкладчик через 5 лет,положив 25000 рублей.(с капитализацией)

Задача.(с экономической формулой)

Вкладчик открыл счет и положил на него сумму в 25000 р. сроком на 4 года под простые (без капитализации) проценты по ставке 11,5 % годовых. Какой будет сумма, которую вкладчик получит при закрытии вклада? На сколько рублей вырастет вклад за 4 года? Чему равен коэффициент наращения (то есть на сколько процентов вырастет сумма вклада)?

В банке получена ссуда в размере 40 тыс. долл. США на 8 лет на следующих условиях: для первых трех лет процентная ставка равна 28% годовых, на следующий год она увеличивается на 2%, и на последующие годы еще на 2,5%. Найдите сумму, которая должна быть возвращена банку по окончании срока ссуды при ежегодных начислениях сложных процентов.

( Сложный процент (или по-другому “процент на процент”) – это такое увеличение капитала, когда накопленная за первый период сумма прибавляется к первоначальной, то есть, говоря экономическим языком, первоначальная сумма капитализируется, и в новом периоде процент будет начисляться уже на новую, увеличенную сумму.)

Решение.

Разобьем весь срок на периоды равной годовой процентной ставки. В первый период идет начисление % годовых, длина периода – лет, потом лет идет начисление годовых, и в третий период продолжительностью года идет начисление и т.д. Тогда за первый период будет начислена следующая сумма:

, за второй и третий соответственно

Значит, по прошествии лет наращенная сумма равна

В нашей задаче три периода. В первый период идет начисление 28% годовых, длина периода – 3 года, потом 1 год идет начисление 30%, и в третий период – 4 года – идет начисление 32,5%. Тогда за первый период будет начислена следующая сумма:

Сумма возврата равна 336,122 тыс. долл. США с точностью до доллара.

Задача №19 ЕГЭ ( вариант №83 )

В банк помещена сумма 3900 тысяч рублей под 50 % годовых.В конце каждого из первых четырех лет хранения после вычисления процентов вкладчик дополнительно вносил на счет одну и ту же фиксированную сумму.К концу пятого года после начисления процентов оказалось,что размер вклада увеличился по сравнению с первоначальным на 725%.Какую сумму вкладчик ежегодно добавил к вкладу?

50%  годовых означает, что каждый год сумма на счету вкладчика увеличивается в 1,5 раза. Будем рассуждать совсем просто. Если вкладчик ничего бы не добавлял к первоначальной  сумме, то через год на его счету было бы  3900·1,5 , через два года -  3900·1,5 2  и так далее.

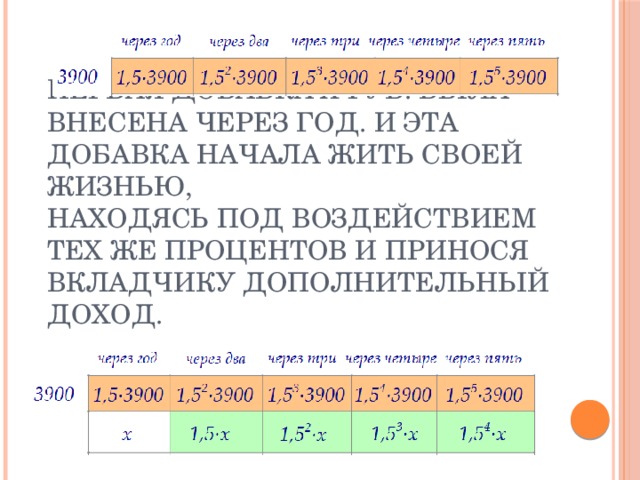
Первая добавка  х  руб. была внесена через год. И эта добавка начала жить своей жизнью,  находясь под воздействием тех же процентов и принося вкладчику дополнительный доход.

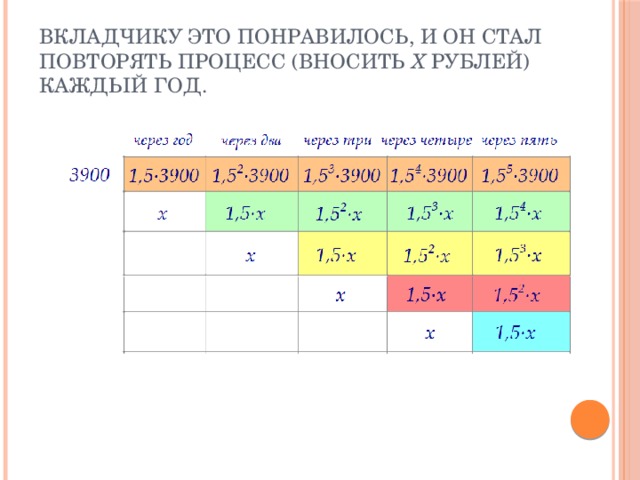
Вкладчику это понравилось, и он стал повторять процесс (вносить  х  рублей) каждый год.

Известно, что размер вклада увеличился по сравнению с первоначальным на  725% .  Это значит, что он стал составлять  825%  от начального, т.е. увеличился в  8,25  раз. Сумма всех слагаемых последнего столбика в  8,25  раз больше, чем  3900  тыс.руб.:

Ответ : 210 тысяч рублей

Задача №19 (вариант№91)

Два брокера купили акции одного достоинства на сумму

3640 р. Когда цена на эти акции возросла, они продали часть акций на сумму 3927 р. Первый брокер продал 75% своих акций, а второй – 80% своих. При этом сумма от продажи акций, полученная вторым брокером, на 140% превысила сумму, полученную первым брокером. На сколько процентов возросла цена одной акции?

Так как сумма от продажи акций, полученная вторым брокером, на 140% больше, то и число проданных вторым брокером акций на 140% больше (цена постоянна).

Обозначим число акций первого брокера (4х), 75% от этого числа равны (3х). Обозначим число акций второго брокера (5y), 80% от этого числа равны (4y).

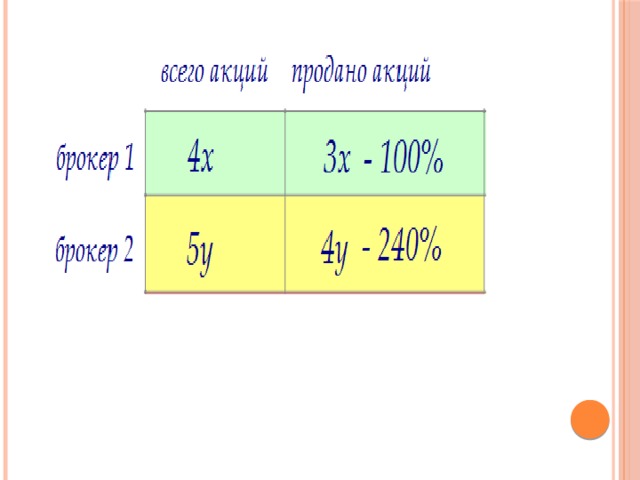
Отсюда легко найти отношение х к y:

Обозначим x = 5t, y = 9t (снова избегаем дробей). Получим:

Можем теперь посчитать общее число купленных и выгодно проданных акций:

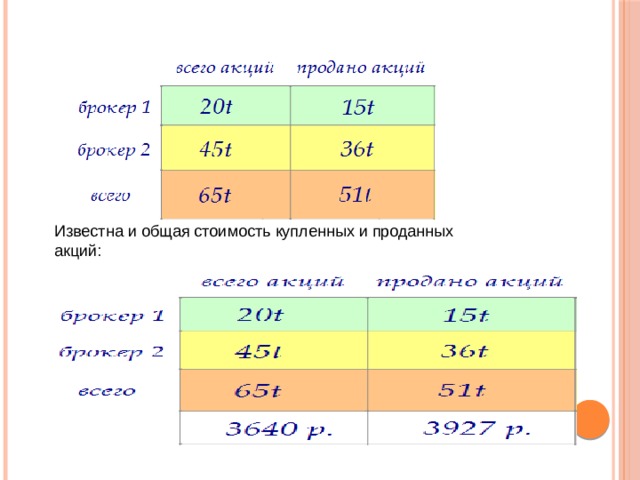
Известна и общая стоимость купленных и проданных акций:

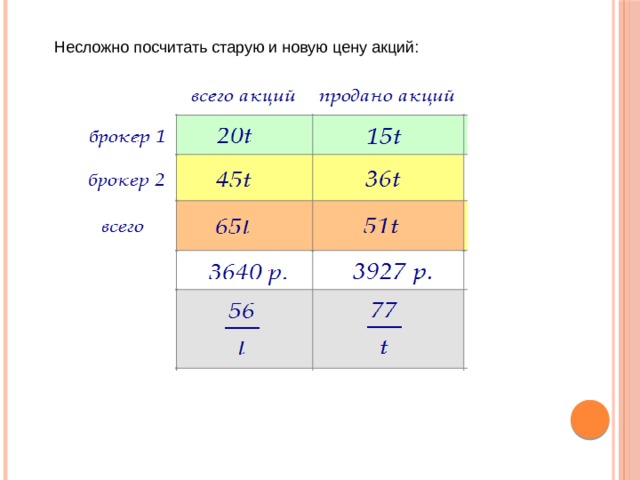
Несложно посчитать старую и новую цену акций:

Задача теперь сводится к такой: на сколько процентов 77 больше 56?

Ответ : 37,5%

Задача №19 (вариант№ 90)

Транснациональная компания "Amoco inc." решила провести недружественное поглощение компании "First Aluminum Company" (FAC) путем скупки акций миноритарных акционеров. Известно, что Amoco inc. было сделано три  предложения владельцам акций FAC, при этом цена покупки одной акции  каждый раз повышалась на 1/3, а общее количество приобретенных  Amoco inc. акций поглощаемой компании увеличивалось на 20%. Определите величину третьего предложения и общее количество  скупленных акций "First Aluminum Company", если начальное  предложение составило $27 за одну акцию, а количество акций,  выкупленных по второй цене, — 15 тысяч.

Уберём лишние слова и сформулируем задачу немного короче:

Было сделано три предложения, при этом цена покупки одной акции каждый раз повышалась на 1/3, а общее количество приобретенных акций увеличивалось на 20%. Начальное предложение составило $27 за одну акцию, а число акций, выкупленных по второй цене, - 15 тыс. Определите величину третьего предложения и общее количество  скупленных акций.

1) Первая цена была равна 27 долларов за одну акцию. 2) Вторая цена на треть больше: 27 + 9 = 36 (долларов). 3) Третья цена ещё на треть больше: 36 + 12 = 48 (долларов) ============================================= Второй раз было куплено 15 тысяч акций, Тем самым общее число акций  увеличилось на 20%. Это значит, что 15 тысяч - это 20% того, что было. Иначе говоря, 15 тыс. - пятая часть числа акций, купленный первый раз. 15 · 5 = 75 (тысяч) - было куплено первый раз.

Теперь общее число акций равно 75 + 15 = 90 (тыс.) В третий раз это число вновь увеличивают на 20%. Значит, в третий раз покупают 90 : 5 = 18 (тыс.) Общее число акций теперь 90 + 18 = 108 (тыс.) Считаем величину третьего предложения: 48 · 18000 = 864000 Ответ : 864000, 108000

Задача №19(вариант №88)

В январе 2000 года ставка по депозитам в банке «Возрождение» составляла  х%  годовых,  тогда как в январе 2001 года -  y%  годовых, причем известно, что  x + y = 30% .  В январе 2000 года вкладчик открыл счет в банке «Возрождение», положив на него  некоторую сумму. В январе 2001 года, по прошествии года с того момента, вкладчик  снял со счета пятую часть этой суммы. Укажите значение x при котором сумма  на счету вкладчика в январе 2002 года станет максимально возможной

Положим в банк  5  рублей, чтобы потом легче было забрать  1  рубль. Через год вклад вырос в  k  раз и стал равен ( 5k ) рублей. Заберём  1  рубль и оставим в банке ( 5k - 1 ) рубль. Через год вклад вырос в  р  раз и стал  р(5k - 1) . Требуется найти наибольшее значение именно этого выражения. Переменные k и p связаны между собой равенством  k + p = 2,3 .

Легко представить, например, пару ставок 10% и 20%. 1,1 + 1,2 = 2,3. Возможны и другие варианты: 11,2% и 18,8%. 1,112 + 1,188 = 2,3. ======================================                                                                                                                        

СПАСИБО ЗА ВНИМАНИЕ!!!