Экономические задачи ЕГЭ (задачи с развернутым ответом)

Экономические задачи ЕГЭ (задачи с развернутым ответом)

Учитель математики

МАОУ СОШ №1- «Школа Сколково-Тамбов»

Беляева Ольга Петровна

• Начиная с 2015 года, в заданиях ЕГЭ по математике профильного уровня появилась новая практико-ориентированная задача №17, так называемая «банковская» задача. В данных задачах учащимся предлагается ознакомиться с разными схемами выплаты кредита банку со стороны заемщика.

Подготовительная работа:

Подготовительная работа:

Подготовительная работа:

Кредит, долг, выплаты… примеры задач

Ответ: 7

Ответ: 6

Кредит, долг, выплаты…

Решение:

год

2016

долг

2017

долг +%

2018

выплата

остаток

2019

1,15 S - 0,8 S

0,8 S

S

1,15 S

0,8 S

0,5 S

1,15∙0,8 S

1,15∙0,8 S – 0,5 S

1,15∙0,5 S – 0,1 S

0,1 S

1,15∙0,5 S

0,5 S

0,1 S

1,15∙0,1 S

1,15∙0,1 S

0

Кредит, долг, выплаты… решите самостоятельно

Ответ: 12 млн рублей

Одинаковые выплаты ( аннуитетный платеж )

примеры задач

Нахождение количества лет выплаты кредита

Ответ: 6 лет

Нахождение суммы кредита

Ответ: 9282000 рублей

Нахождение ежегодного транша

Ответ : 3703860 рублей .

Одинаковые выплаты (аннуитетный платеж)

Решение: пусть S –сумма кредита; обозначим ежегодную выплату а=2928200 руб

год

долг

15

долг +%

16

вып

17

лата

18

остаток

1,1 S

1,1 S -а

а

S

1,1∙(1,1 S –а)

1,1 S -а

1,1∙(1,1 S –а) -а

а

1,1∙(1,1∙(1,1 S –а) –а)

1,1∙(1,1 S –а) -а

1,1∙(1,1∙(1,1 S –а) –а) –а

а

1,1∙(1,1∙(1,1∙(1,1 S –а) –а) –а) –а

1,1∙(1,1∙(1,1∙(1,1 S –а) –а) –а)

1,1∙(1,1∙(1,1 S –а) –а) –а

а

а

1,1∙(1,1∙(1,1∙(1,1 S –а) –а) –а) –а=0

⇒

Одинаковые выплаты (аннуитетный платеж)

решите самостоятельно

Ответ: 162000 рублей

Уменьшение ежегодного долга на одну и туже величину ( дифференцированный платеж )

примеры задач

Ответ: 27,3 млн. руб.

Ответ: 5 лет

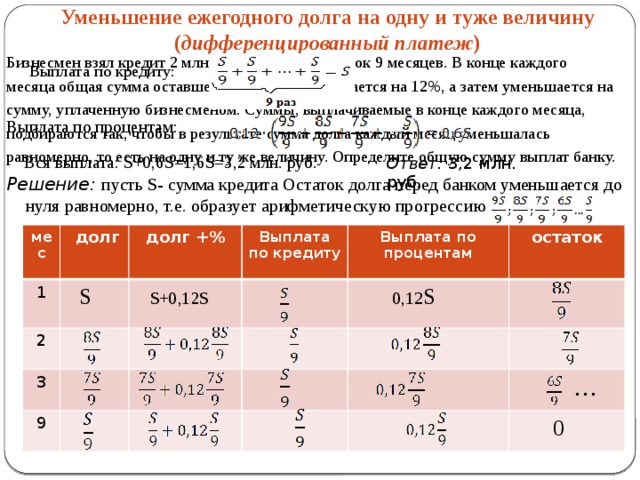
Уменьшение ежегодного долга на одну и туже величину ( дифференцированный платеж )

Бизнесмен взял кредит 2 млн рублей в банке на срок 9 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 12%, а затем уменьшается на сумму, уплаченную бизнесменом. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Определите общую сумму выплат банку.

Выплата по кредиту:

Выплата по процентам:

Вся выплата: S+0,6S=1,6S=3,2 млн. руб.

Ответ: 3,2 млн. руб.

Решение: пусть S- сумма кредита Остаток долга перед банком уменьшается до нуля равномерно, т.е. образует арифметическую прогрессию

мес

1

долг

2

долг +%

Выплата по кредиту

3

9

Выплата по процентам

остаток

0,12 S

S

S+0,12S

…

0

Уменьшение ежегодного долга на одну и туже величину ( дифференцированный платеж )

решите самостоятельно

Алексей решил взять кредит в банке100 тыс. рублей на 4 месяца под 5% в месяц. Существует две схемы выплаты кредита. По первой схеме банк в конце каждого месяца начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на 5 %), затем Алексей переводит в банк фиксированную сумму и в результате выплачивает весь долг четырьмя равными платежами. По второй схеме тоже сумму долга в конце каждого месяца увеличивается на 5%, а затем уменьшается на сумму, уплаченную Алексеем. Суммы, выплачиваемые в конце каждого месяца подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, т.е. на одну и ту же величину. Какую схему выгоднее выбрать Алексею? Сколько рублей будет составлять эта выгода. Результат округлите до сотых.

Ответ. Вторая схема; 304,73 рублей.

ЕГЭ-18г № 17

Ответ: 800 000 руб.

Источники

• Практико-ориентированные задачи в заданиях ЕГЭ по математике : сборник экономических задач / сост. Г. М. Конева. – Улан-Удэ: Издательство Бурятского государственного университета, 2017
• Математика. ЕГЭ. Задача с экономическим содержанием: учебно-методическое пособие/ Под. ред. Ф.Ф.Лысенко и С.Ю. Кулабухова. – Ростов н/Д: Легион, 2016.
• Колесникова С.И. Экономические задачи ЕГЭ/ С.И. Колесникова. –М.: ООО «Азбука-2000», 2016.
• http://alexlarin.net
• https://ege.sdamgia.ru/
• https://neznaika.pro