Эффективные способы решения квадратных уравнений
Г.С.Адылгазина,
учитель математики
Задачей любого учителя математики является правильное и локоничное решение задач. Многие задачи и уравнения сводятся к решению квадратных уравнений. Поэтому необходимо научить учащихся использованию эффективных способов решения квадратных уравнений. В этой связи, я считаю, после введения понятия квадратного уравнения, решения неполных квадратных уравнений и решения квадратных уравнений с помощью дискрименанта, необходимо больше времени уделить на использование теоремы Виета.
С помощью теоремы Виета можно сразу же решить задачи такого типа: «Найдите длины сторон прямоугольника, если его периметр равен 28 см, а площадь – 48 см².» Если учесть, что
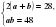 или
или 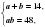
и что система уравнений является симметрической, путем подбора получаем два решения a=6 cм, b= 8см или a=8 cм, b= 6см.
В школьном курсе чаще всего используют теорему Виета для приведенных квадратных уравнений вида 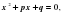 но можно расширить знания учащихся, если вспомнить, что это уравнение получилось из уравнения
но можно расширить знания учащихся, если вспомнить, что это уравнение получилось из уравнения 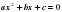 при почленном делении каждого слагаемого на ненулевой коэффициент а. Таким образом, получаем уравнение вида
при почленном делении каждого слагаемого на ненулевой коэффициент а. Таким образом, получаем уравнение вида 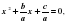 где
где 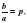
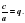 Поэтому для того, чтобы решить неприведенное квадратное уравнение, надо составить следующую систему уравнений:
Поэтому для того, чтобы решить неприведенное квадратное уравнение, надо составить следующую систему уравнений:
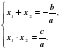
Далее замечаем, что сумма корней квадратного уравнения представлена в виде обыкновенной дроби со знаменателем а. Тогда можно предположить, что и корни квадратного уравнения – обыкновенные дроби с тем же знаменателем. При этом учитываем, что произведением обыкновенных дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей. Поэтому преобразуем дробь 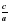 , умножив и числитель, и знаменатель на а:
, умножив и числитель, и знаменатель на а:
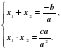
В таком случае –b будет равен сумме числителей корней квадратного уравнения, а произведение c·a равно числителей этих корней.
Рассмотрим этот способ на примере. Решим уравнение 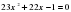 . Разделим уравнение на 23 и получим уравнение
. Разделим уравнение на 23 и получим уравнение 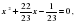 по обратной теореме Виета:
по обратной теореме Виета:
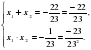
Если представим корни уравнения в виде обыкновенных дробей со знаменателями 23, то есть 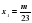 и
и 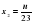 , тогда
, тогда 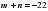 и
и
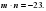 Значит,
Значит, 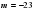 и
и 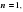 поэтому
поэтому 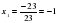 , а
, а 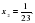
Ответ: 
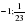
Некоторые квадратные уравнения можно очень быстро решить, если воспользоваться так называемыми алгоритмами.
І алгоритм. Если 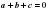 , то
, то 

ІІ алгоритм. Если  , то
, то 

Запомнить эти алгоритмы очень легко. Если сумма коэффициентов без изменения знаков равна нулю, то первый корень квадратного уравнения равен 1, а второй вычисляется по формуле  Если же при изменении знака второго коэффициента сумма коэффициентов равна нулю, то первый корень квадратного уравнения равен -1, а второй вычисляется по формуле
Если же при изменении знака второго коэффициента сумма коэффициентов равна нулю, то первый корень квадратного уравнения равен -1, а второй вычисляется по формуле  То есть при изменении знака второго коэффициента изменяем знак везде.
То есть при изменении знака второго коэффициента изменяем знак везде.
Рассмотренный выше уравнение 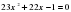 можно легко решить по второму алгоритму:
можно легко решить по второму алгоритму:
 , то есть
, то есть  . Тогда
. Тогда 

При объяснении данных алгоритмов желательно предложить учащимся найти какой-нибудь корень уравнения (ими будут 1 или -1). Второй же корень легко находится из второго уравнения системы теоремы Виета
 Если первый корень равен 1, то
Если первый корень равен 1, то  то есть
то есть  Если же первый корень равен -1, то соответственно -
Если же первый корень равен -1, то соответственно - то есть
то есть 
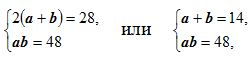


 Получите свидетельство
Получите свидетельство Вход
Вход


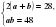 или
или 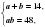
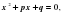 но можно расширить знания учащихся, если вспомнить, что это уравнение получилось из уравнения
но можно расширить знания учащихся, если вспомнить, что это уравнение получилось из уравнения 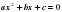 при почленном делении каждого слагаемого на ненулевой коэффициент а. Таким образом, получаем уравнение вида
при почленном делении каждого слагаемого на ненулевой коэффициент а. Таким образом, получаем уравнение вида 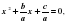 где
где 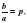
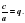 Поэтому для того, чтобы решить неприведенное квадратное уравнение, надо составить следующую систему уравнений:
Поэтому для того, чтобы решить неприведенное квадратное уравнение, надо составить следующую систему уравнений: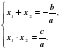
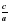 , умножив и числитель, и знаменатель на а:
, умножив и числитель, и знаменатель на а: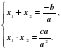
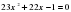 . Разделим уравнение на 23 и получим уравнение
. Разделим уравнение на 23 и получим уравнение 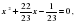 по обратной теореме Виета:
по обратной теореме Виета: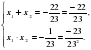
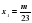 и
и 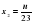 , тогда
, тогда 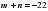 и
и
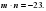 Значит,
Значит, 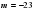 и
и 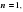 поэтому
поэтому 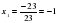 , а
, а 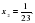
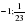
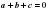 , то
, то 








 Эффективные способы решения квадратных уравнений (61.49 КB)
Эффективные способы решения квадратных уравнений (61.49 КB)
 0
0 576
576 96
96 Нравится
0
Нравится
0


