Цели урока:
обучающие:
актуализировать умение решать уравнения как аналитически, так и графически,
развивающие:
развивать умение учащихся систематизировать учебный материал, развивать коммуникативную культуру,
воспитывающие:
формировать у учащихся интерес к предмету.
Тип урока: урок обобщения изученного материала
Технология уровневой дифференциации обучения на основе обязательных результатов
Номинация – эффективная реализация основного содержания урока
План урока
организационный момент,
актуализация теоретических знаний по теме,
постановка цели занятия перед учащимися, объявление темы урока,
практическая работа на построение графиков изученных функций и применение их для решения уравнений,
повторение алгоритма аналитического способа решения уравнений (памятка для учащихся, имеющих трудности в обучении),
диагностика усвоения материала по теме (разноуровневая самостоятельная работа),
запись домашнего задания (пояснения),
подведение итогов урока.
Оборудование
Мультимедийные средства обучения, раздаточные материалы.
Ход урока
Организационный момент, характеризующийся внешней и внутренней (психологической) готовностью к уроку.
(Перед уроком приготовить раздаточный материал, предусмотреть наличие линеек, карандашей).
Актуализация теоретических знаний по теме «Решение уравнений»
Учащимся предлагается тест-разминка «Проверь себя» - продолжительностью 5-6 минут (приложение 1). Проверка правильности выполнения осуществляется непосредственно самими учащимися через показ ответов на слайде. Учащиеся имеют возможность оценить свою подготовку к уроку (Критерии оценки прилагаются).
Приложение 1. (Данный раздаточный материал предлагается учащимся без ответов)
Постановка цели занятия перед учащимися, объявление темы урока.
(Показ слайда, учащиеся отражают тему урока в тетрадях)
Практическая работа на построение графиков изученных функций и применение их для решения уравнений, систем уравнений. На стенде к уроку висят справочные таблицы с порядком построения графиков отдельных функций, однако на них учитель не указывает. Слабоуспевающие дети, как правило, используют их в работе на уроке.(Данные таблицы приведены в конце)
Показ последовательно слайдов с заданиями:
Построение графика линейной функции вида y = kx + b;
Построение графика квадратичной функции y = ax2 + bx + c, a ≠ 0;
Построение графика обратной пропорциональности y = k / x, x ≠ 0;
Решение конкретных уравнений графическим способом (Приложение 2).
Приложение 2.
Построение графика линейной функции вида y = kx + b
График линейной функции – прямая, прямую строят по 2-м точкам (см. аксиому геометрии)
Например, y = -2x + 3
Постройте данную прямую на координатной плоскости в рабочих тетрадях.
Построение графика квадратичной функции y = ax2 + bx + c, a ≠ 0
График квадратичной функции - …, кривая, поэтому надо иметь для построения много точек, более трех.
Например, y = (x – 2)2 + 1. Используем обычную параболу y = x2 Сдвинем ее на 2 единицы вправо, затем на единицу вверх.
Постройте данную параболу в рабочих тетрадях.
Повторение алгоритма аналитического способа решения уравнений (памятка для учащихся, имеющих трудности в обучении).
Показ слайда с памятками (Приложение 3 – памятки).
Приложение 3.
Памятка для решения квадратных уравнений (любых)
Выписать a, b, c
Найти по формуле дискриминант
Найти корни уравнения по формуле корней
Памятка для решения квадратных уравнений (с четным b)
Выписать a, b, c
Найти по формуле дискриминант, деленный на 4 (D1)
Найти корни уравнения по частной формуле корней через D1
Памятка для решения приведенных квадратных уравнений способом подбора по теореме, обратной теореме Виета
Записать сумму корней и их произведение на основе теоремы
Угадать корни квадратного уравнения, обладающие выше перечисленными свойствами
Памятка для решения рациональных уравнений
Биквадратных
Ввести новую переменную (y = x2)
Решить как обычное квадратное уравнение с переменной y
Вернуться к исходной переменной, решив уравнения y = x2
Рациональных
Разложить все знаменатели дробей на множители
Избавиться от деления умножением на общий знаменатель всех дробей, при этом учесть ОДЗ
Решить целое уравнение и проверить корни с учетом ОДЗ
Распечатанные памятки можно предложить учащимся, которые претендуют на «3»
Разноуровневая самостоятельная работа
Приложение 4 (критерии оценки и ответы через демонстрацию слайда)
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



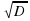 - иррациональное число
- иррациональное число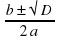
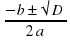
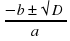
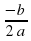 , т.е. xв = …, yв = …
, т.е. xв = …, yв = … 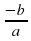 ; x1 ∙ x2 =
; x1 ∙ x2 = 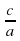
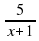 +
+  =
= 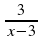
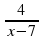 =
= 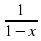
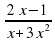
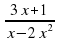
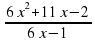 = 0
= 0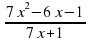 = 0
= 0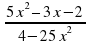
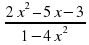
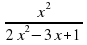 -
- 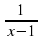
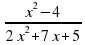 +
+ 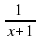









 Решение линейных, квадратных, рациональных уравнений (35.79 КB)
Решение линейных, квадратных, рациональных уравнений (35.79 КB)
 0
0 881
881 102
102 Нравится
0
Нравится
0


