Движение

Движение плоскости   – это отображение плоскости на себя, сохраняющее расстояния.

Осевая симметрия - -  преобразование, при котором каждая точка А фигуры (или тела) преобразуется в симметричную ей относительно некоторой оси  а точку А1.

Центральная симметрия - преобразование, переводящее каждую точку А фигуры (тела) в точку А1, симметричную ей относительно центра О.

Скользящая симметрия - называется такое преобразование, при котором последовательно выполняются осевая симметрия и параллельный перенос.

Движение

Рыженко Елена Владимировна,

учитель математики и информатики

МБОУ г. Астрахани «СОШ № 64»

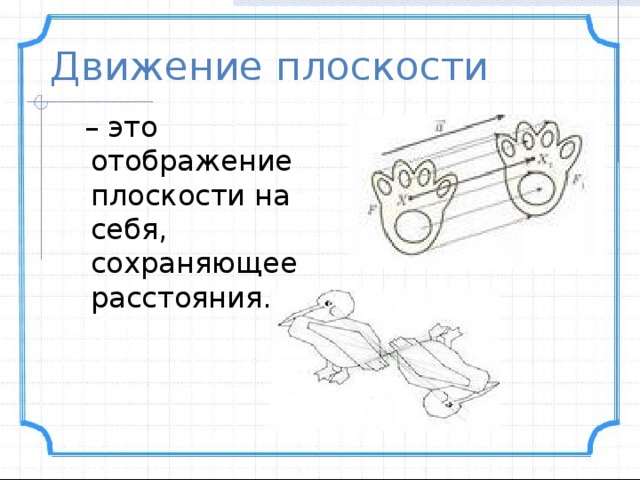
Движение плоскости

– это отображение плоскости на себя, сохраняющее расстояния.

Виды движения

Симметрия

осевая

центральная

скользящая

зеркальная

Параллельный перенос

Поворот

Осевая симметрия

а

- преобразование, при котором каждая точка А фигуры (или тела) преобразуется в симметричную ей относительно некоторой оси а точку А1.

А

А1

Осевая симметрия в природе и архитектуре

Центральная Симметрия

- преобразование, переводящее каждую точку А фигуры (тела) в точку А1, симметричную ей относительно центра О

В

О

А1

А

В1

Примеры центральной симметрии

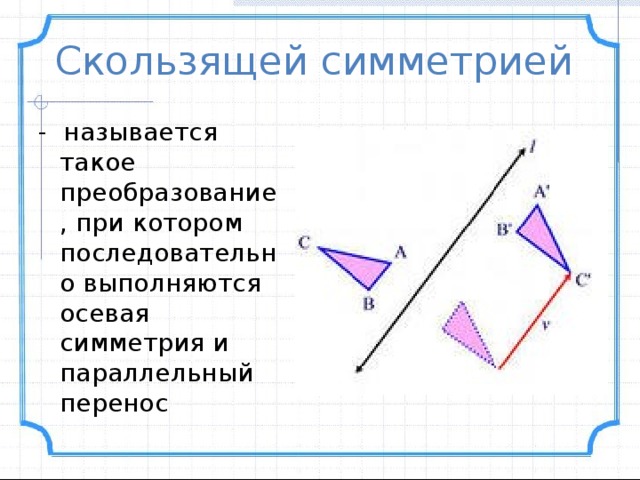
Скользящей симметрией

- называется такое преобразование, при котором последовательно выполняются осевая симметрия и параллельный перенос

Примеры скользящей симметрии

Зеркальная симметрия

Если преобразование симметрии относительно плоскости переводит фигуру (тело) в себя, то фигура называется симметричной относительно плоскости, а данная плоскость – плоскостью симметрии этой фигуры.

Зеркальная симметрия в природе

Параллельный перенос

― частный случай движения, при котором все точки пространства перемещаются в одном и том же направлении на одно и то же расстояние. Иначе, если M ― первоначальное, а M' ― смещенное положение точки, то вектор M’ ― один и тот же для всех пар точек, соответствующих друг другу в данном преобразовании.

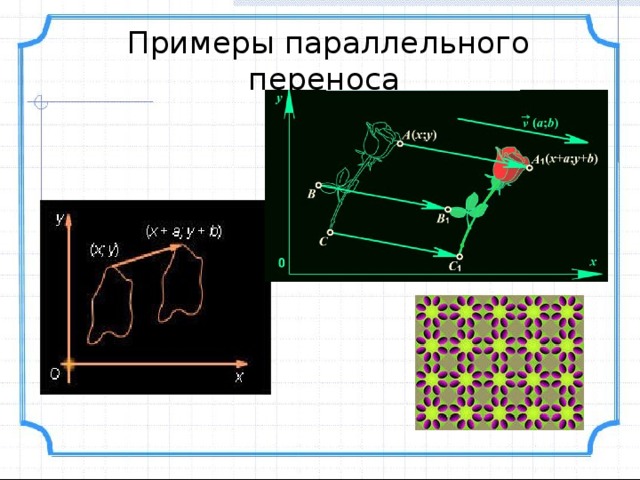
Примеры параллельного переноса

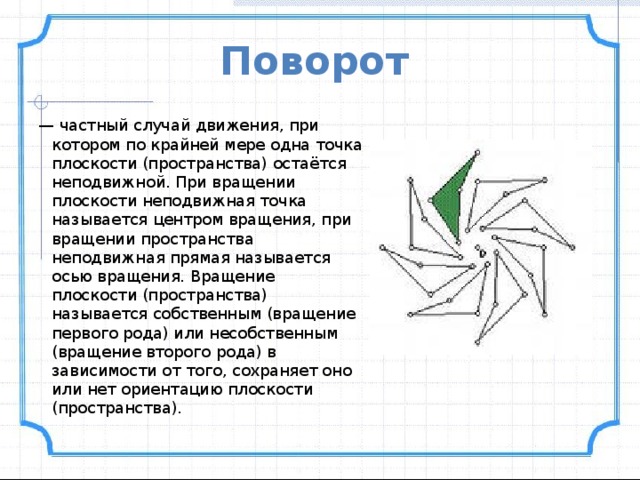
Поворот

— частный случай движения, при котором по крайней мере одна точка плоскости (пространства) остаётся неподвижной. При вращении плоскости неподвижная точка называется центром вращения, при вращении пространства неподвижная прямая называется осью вращения. Вращение плоскости (пространства) называется собственным (вращение первого рода) или несобственным (вращение второго рода) в зависимости от того, сохраняет оно или нет ориентацию плоскости (пространства).

Примеры поворота

Источники информации

dic.academic.ru

http://im3-tub-ru.yandex.net/i?id=435852834-20-72&n=21

http://im5-tub-ru.yandex.net/i?id=140806084-30-72&n=21

http://im7-tub-ru.yandex.net/i?id=150794693-34-72&n=21

http://im4-tub-ru.yandex.net/i?id=212733813-47-72&n=21

http://im6-tub-ru.yandex.net/i?id=138969236-56-72&n=21

http://im8-tub-ru.yandex.net/i?id=33271537-02-72&n=21

http://im5-tub-ru.yandex.net/i?id=12595952-28-72&n=21

http://im6-tub-ru.yandex.net/i?id=168438411-65-72&n=21

http://im4-tub-ru.yandex.net/i?id=137224307-54-72&n=21

http://im0-tub-ru.yandex.net/i?id=419203152-54-72&n=21

http://im6-tub-ru.yandex.net/i?id=332531799-65-72&n=21

http://im0-tub-ru.yandex.net/i?id=435873928-66-72&n=21

http://im4-tub-ru.yandex.net/i?id=221340753-70-72&n=21

http://im0-tub-ru.yandex.net/i?id=119470133-54-72&n=21

http://im7-tub-ru.yandex.net/i?id=192004086-70-72&n=21

http://im3-tub-ru.yandex.net/i?id=21057398-57-72&n=21

http://im7-tub-ru.yandex.net/i?id=131179132-68-72&n=21

http://im7-tub-ru.yandex.net/i?id=190423059-06-72&n=21

http://im8-tub-ru.yandex.net/i?id=146612707-02-72&n=21

http://im8-tub-ru.yandex.net/i?id=328191035-13-72&n=21

http://school.xvatit.com/images/2/25/22-06-141.jpg