Введение
В последние годы в заданиях части С3 ЕГЭ по информатике часто встречаются задачи, которые решаются методом динамического программирования. Это и явилось основным критерием выбора данной темы для доклада.
Основная цель данной работы – ознакомить с основами методов математического программирования, необходимого для решения теоретических и практических задач.
Для достижения поставленной цели необходимо решить ряд задач:
- рассмотреть понятие «динамическое программирование»;
- показать механизм решения задач части С3 ЕГЭ по информатике и ИКТ при помощи динамического программирования;
- сделать выводы по результатам работы.
Динамическое программирование
Решение задач математического программирования, которые могут быть представлены в виде многошагового (многоэтапного) процесса, составляет предмет динамического программирования. Вместе с этим динамическим программированием называют особый математический метод оптимизации решений, специально приспособленный к многошаговым процессам. Многошаговым обычно считают процесс, развивающийся во времени и распадающийся на ряд «шагов», или «этапов». Однако метод динамического программирования используется и для решения задач, в которых время не фигурирует. Некоторые процессы распадаются на шаги естественно (например, процесс планирования хозяйственной деятельности предприятия на отрезок времени, состоящий из нескольких лет); многие процессы можно разделить на этапы искусственно.
Одна из особенностей метода динамического программирования состоит в том, что принятие решения по отношению к многошаговым процессам рассматривается не как единичный акт, а как целый комплекс взаимосвязанных решений. Эту последовательность взаимосвязанных решений называют стратегией. Цель оптимального планирования – выбрать стратегию, обеспечивающую получение наилучшего результата с точки зрения заранее выбранного критерия. Такую стратегию называют оптимальной.
Суть метода динамического программирования состоит в том, что вместо поиска оптимального решения сразу для всей сложной задачи предпочитают находить оптимальные решения для нескольких более простых задач аналогичного содержания, на которые расчленяется исходная задача.
Другой важной особенностью метода динамического программирования является независимость оптимального решения, принимаемого на очередном шаге, от предыстории, т. е. от того, каким образом оптимизируемый процесс достиг теперешнего состояния. Оптимальное решение выбирается лишь с учетом факторов, характеризующих процесс в данный момент. Так, при выборе кратчайшего пути, ведущего из некоторого промежуточного пункта в конечный, водитель автомобиля принимает решение независимо от того, как, когда и какой дорогой он прибыл в данный пункт, руководствуется лишь расположением этого пункта в общей схеме дорог
Метод динамического программирования характеризуется также тем, что выбор оптимального решения на каждом шаге должен производиться учетом его последствий в будущем. Это означает, что, оптимизируя процесс на каждом отдельном шаге, ни в коем случае нельзя забывать обо всех последующих шагах. Таким образом, динамическое программирование – это дальновидное планирование, планирование с учетом перспективы. Из всего сказанного следует, что поэтапное планирование многошагового процесса должно производиться так, чтобы при планирование каждого шага учитывалась не выгода, получаемая только на данном шаге, а общая выгода, получаемая по окончании всего процесса, и именно относительно общей выгоды производится оптимальное планирование. Этот принцип выбора решения в динамическом программировании является определяющим и носит название принципа оптимальности. Оптимальная стратегия обладает темп свойством, что, каковы бы ни были первоначальное состояние и решение, принятое в начальный момент, последующие решения должны составлять оптимальную стратегию относительно состояния, являющего результатом первоначального решения.
При решении оптимизационной задачи методом динамического программирования необходимо учитывать на каждом шаге последствия, к которым приведет в будущем решение, принимаемое в данный момент. Исключением является последний шаг, которым процесс заканчивается. Здесь процесс можно планировать таким образом, чтобы последний шаг сам по себе приносил максимальный эффект. Спланировав оптимальным образом последний шаг, можно к нему «пристраивать» предпоследний так, чтобы результат этих двух шагов был оптимальным, и т. д. Именно так – от конца к началу – и можно развернуть процедуру принятия решений. Но чтобы принять оптимальное решение на последнем шаге, надо знать, чем мог закончиться предпоследний шаг. Значит, надо сделать разные предположения о том, чем мог закончиться предпоследний шаг и для каждого из предположений найти решение, при котором эффект на последнем шаге был бы наибольшим. Такое оптимальное решение, найденное при условии, что предыдущий шаг закончился определенным образом, называют условно – оптимальным.
Аналогично оптимизируется решение на предпоследнем шаге, т. е. делаются все возможные предположения о том, чем мог завершиться шаг, предшествующий предпоследнему, и для каждого из возможных исходов выбирается такое решение на предпоследнем шаге, чтобы эффект за последние два шага (их которых последний уже оптимизирован) был наибольшим и т. д.
Таким образом, На каждом шаге в соответствии с принципом оптимальности ищется решение, обеспечивающее оптимальное продолжение процесса относительно состояния, достигнутого в данный момент. Если при движении от конца к началу оптимизируемого процесса определены условно – оптимальные решения для каждого шага и вычислен соответствующий эффект (эту стадию рассуждений называют иногда условной оптимизацией), то остается «пройти» весь процесс в прямом направлении (стадия безусловной оптимизации) и «прочитать» оптимальную стратегию, которая нас интересует.
В принципе динамическое планирование может разворачиваться и в прямом направлении, т. е. от первого шага процесса к последнему.
Практическое применение динамического программирования
Типовой алгоритм решения задач методом динамического программирования:
Описать строение оптимальных решений.
Выписать рекуррентное соотношение, связывающие оптимальные значения параметра для подзадач.
Двигаясь снизу вверх, вычислить оптимальное значение параметра для подзадач.
Пользуясь полученной информацией, построить оптимальное решение.
Рассмотрим задания С3 ЕГЭ по информатике и ИКТ.
Задача 1. У исполнителя Утроитель две команды, которым присвоены номера:
1. прибавь 1
2. умножь на 3
Первая из них увеличивает число на экране на 1, вторая – утраивает его Программа для Утроителя – это последовательность команд. Сколько есть программ, которые число 1 преобразуют в число 20? Ответ обоснуйте.
Весь материал - смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход


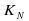 обозначим количество программ для получения числа N, для N1
обозначим количество программ для получения числа N, для N1 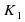 =1 . Рассмотрим, сколькими способами можно получить из числа 1 числа 2, 3, 4, 5, 6, … и определим рекуррентную формулу определения количества программ для получения числа N.
=1 . Рассмотрим, сколькими способами можно получить из числа 1 числа 2, 3, 4, 5, 6, … и определим рекуррентную формулу определения количества программ для получения числа N.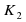 =1 , 1+1=2
=1 , 1+1=2 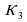 =2 ,K2+1=1+1+1 или 1*3
=2 ,K2+1=1+1+1 или 1*3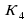 =2 ,
=2 , 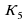 =2 ,
=2 , 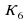 =3 ,
=3 , 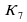 =
=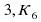 +1 =1+1+1+1+1+1+1+1+1 или 1*3+1+1+1+1 или 1*3+1*3+1
+1 =1+1+1+1+1+1+1+1+1 или 1*3+1+1+1+1 или 1*3+1*3+1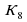 =3 ,
=3 , 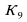 =5,
=5, 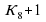 =1+1+1+1+1+1+1+1+1 или 1*3 +1+1+1+1+1+1 или 1*3+1*3+1*3 или 1*3+1*3+1+1+1 или 1*3*3 и.т.д .
=1+1+1+1+1+1+1+1+1 или 1*3 +1+1+1+1+1+1 или 1*3+1*3+1*3 или 1*3+1*3+1+1+1 или 1*3*3 и.т.д .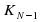
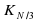
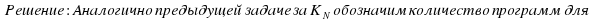 получения числа N, для N1
получения числа N, для N1 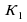 =1
=1 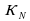 =
=








 Динамическое программирование (49.26 КB)
Динамическое программирование (49.26 КB)
 0
0 2215
2215 247
247 Нравится
0
Нравится
0



