Действительные числа.

Действительные числа

МАОУ Свердловская СОШ № 2 г.о. Лосино-Петровский Московской области

УЧИТЕЛЬ МАТЕМАТИКИ

ЛУГОВАЯ ОЛЬГА АЛЕКСАНДРОВНА

число

• Число́ — одно из основных понятий математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей .

Евклид. Деталь «Афинской школы» Рафаэля

НАТУРАЛЬНЫЕ ЧИСЛА

• Первые числа, с которыми вы познакомились в школе, - это натуральные числа: 1, 2, 3, 4, 5, 6,…… .
• Понятие натуральных чисел возникло из потребностей счёта предметов.
• Множество натуральных чисел обладает тем свойством, что сумма и произведение любых двух натуральных чисел являются натуральными числами, а разность и частное необязательно являются натуральными числами.
• Множество натуральных чисел будем обозначать .

ЦЕЛЫЕ ЧИСЛА

• Множество целых чисел состоит из натуральных чисел , целых отрицательных чисел и числа «нуль» : ………-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5,……….
• Сумма, разность и произведение целых чисел являются целыми числами, а частное не всегда является целым числом.
• Множество целых чисел будем обозначать .

Рациональные числа

• Число называют рациональным, если его можно записать в виде дроби , где
• - числитель дроби, - знаменатель дроби
• Сумма, разность, произведение и частное любых двух рациональных чисел являются рациональными числами.
• Важно: На нуль делить нельзя!!!

ДЕСЯТИЧНЫЕ ДРОБИ –дроби, знаменатель которых есть некоторая степень числа 10.

КОНЕЧНЫЕ

БЕСКОНЕЧНЫЕ ПЕРИОДИЧЕСКИЕ

• Если конечную десятичную дробь записать в виде обыкновенной несократимой дроби, то её знаменатель не имеет других делителей , кроме 2 и 5.
• И наоборот: Если знаменатель несократимой дроби не имеет других простых делителей, кроме 2 и 5, то эта дробь разлагается в конечную десятичную дробь.

• Если знаменатель несократимой дроби имеет простой делитель, отличный от 2 и 5, то эта дробь не разлагается в конечную десятичную дробь, и применив к ней способ деления «уголком» , нельзя получить конечную десятичную дробь.

Каждое рациональное число может быть разложено в бесконечную десятичную периодическую дробь.

Для нахождения этого разложения можно разделить «уголком» числитель дроби на её знаменатель:

, так как

Верно и обратное утверждение: Каждая периодическая дробь есть десятичное разложение обыкновенной дроби (некоторого рационального числа).

Пример. Запишем бесконечную периодическую десятичную дробь 2,1(45) в виде обыкновенной дроби.

Обозначим дробь буквой :

тогда

Таким образом, рациональные числа имеют два представления (две формы записи)- одно в виде дроби

• Множество рациональных чисел обозначают буквой

• Наряду с бесконечными десятичными периодическими дробями существуют и бесконечные десятичные непериодические дроби, которые называют иррациональными числами
• Множество иррациональных чисел обозначают буквой .
• Рациональные и иррациональные числа составляют множество всех действительных чисел , которое обозначают буквой .

R

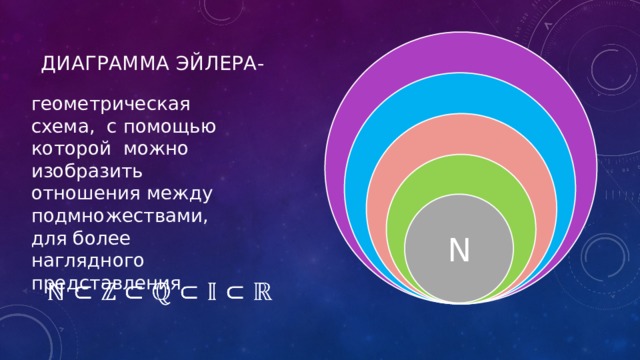
Диаграмма эйлера-

I

геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для более наглядного представления

Q

Z

N

Свойства действительных чисел

Действительные числа обладают следующими свойствами, которые принято располагать по группам:

I. Свойства порядка.

1. Для любых двух действительных чисел и выполняется, и притом только одно, из трёх соотношений: .

1. Для любых двух действительных чисел и выполняется, и притом только одно, из трёх соотношений: .

2.Для любых двух действительных чисел и , таких, что , найдётся такое действительное число , что и , т.е. .

2.Для любых двух действительных чисел и , таких, что , найдётся такое действительное число , что и , т.е. .

3.Если и , то

3.Если и , то

(свойство транзитивности неравенств)

(свойство транзитивности неравенств)

ii. Свойства сложения и вычитания

1. –переместительное свойство сложения

1. –переместительное свойство сложения

2. -сочетательное свойство сложения

2. -сочетательное свойство сложения

3.

3.

4.

4.

5.

5.

6. Если , то для любого .

6. Если , то для любого .

iii. Свойства умножения и деления

1. переместительное свойство умножения

1. переместительное свойство умножения

2. -сочетательное свойство умножения

2. -сочетательное свойство умножения

3.

3.

4.

4.

5.

5.

6.

6.

7.

7.

8. – распределительное свойство

8. – распределительное свойство

9. Если и , то .

9. Если и , то .

iv. Архимедово свойство

Для любых чисел и таких, что существует натуральное число такое, что

Для любых чисел и таких, что существует натуральное число такое, что

V. Свойство непрерывности действительных чисел

Для любой системы отрезков удовлетворяющих условиям:

Для любой системы отрезков удовлетворяющих условиям:

1) ;

1) ;

2) при ,

2) при ,

существует, и притом единственная, точка, принадлежащая всем отрезкам

существует, и притом единственная, точка, принадлежащая всем отрезкам

До новых встреч!

Удачи в освоении предмета!!!