Действия с рациональными числами

Действия с рациональными числами

6 класс

И. Песталоцци

« Счет и вычисления ― основа

порядка в голове»

Оценочный лист

Верные и неверные утвержде

ния

Найти ошибку

Вычислите

Решите уравнения

Итог

Верные и неверные утверждения

1) Верно ли, что чтобы сложить два

отрицательных числа, нужно сложить их

модули?

2) Верно ли, что чтобы сложить числа с

разными знаками, надо: 1) из большего

модуля слагаемых вычесть меньший;

2) поставить перед полученным числом

знак того слагаемого, модуль которого

больше?

Верные и неверные утверждения

3) Верно ли, что чтобы изданного числа

вычесть другое, надо к уменьшаемому

прибавить число, противоположное

вычитаемому?

4) Верно ли, что чтобы перемножить два

отрицательных числа, надо перемножить

их модули и перед полученным числом

поставить знак минус?

Верные и неверные утверждения

5) Верно ли, что чтобы перемножить два

числа с разными знаками, надо

перемножить их модули?

6) Верно ли, что чтобы разделить

отрицательное число на отрицательное,

надо разделить модуль делителя на модуль

делимого?

7) Верно ли, что при делении чисел с разными

знаками, надо: 1) разделить модуль

делимого на модуль делителя; 2) поставить

перед полученным числом знак минус?

Верные и неверные утверждения

1) нет

2) да

3) да

4) нет

5) нет

6) нет

7) да

Найдите ошибку

1) ‒12,6 : 2= 6,3

2) – 18 + (–15) = 33

3) ‒ 3,8 •(– 3) = – 11,4

4) – 3,8 + 1,8 = 2

5) – 6,3 –(– 1,3) = –7,6

6) 7– 27 = 20

7) – 18,2 : (– 9,1) = – 2

8) 8,5 + (– 1,5) = – 7

9) – 9,5 – 0,5 = 10

Расположи ответы в порядке возрастания ты узнаешь имя французского математика , который предложил геометрическое истолкование положительных и отрицательных чисел

1) – 12,6 : 0,2 – 0,8•(– 0,5) Д

2) ( 17,5 – 57,5) : 2,5 К

3) – 28,3 – (– 8,6) •3,1 Р

4) – 0,648 : 0,02 +(– 8,5) : 17 Е

5) – 3,6 – 7,2 : 2 А

6) – 144 : (–12) – 12 Т

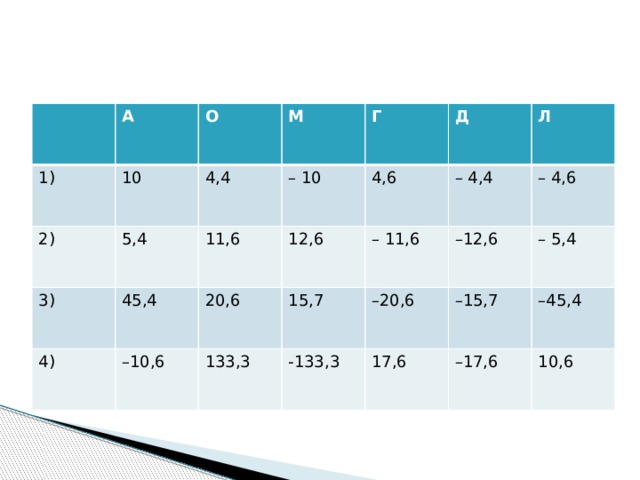
Решите уравнения

1) Х – 2,8 = – 7,2

2) 8,5 – y = – 3,1

3) (х + 12,4) •0,5 = –16,5

4) ( –3,5 –у) : 2 = 6,83

Найдите в таблице для каждого уравнения соответственно правильный ответ.

Каждому правильному ответу соответствует

буква. Расположите буквы

соответственно номеру

уравнения и вы узнаете

как китайские математики

во втором веке до н. э.

называли отрицательные

числа.

А

1)

2)

10

О

М

5,4

3)

4,4

Г

11,6

4)

45,4

– 10

– 10,6

12,6

Д

20,6

4,6

133,3

15,7

– 11,6

Л

– 4,4

-133,3

– 12,6

– 20,6

– 4,6

– 5,4

– 15,7

17,6

– 17,6

– 45,4

10,6

Долг

Отрицательные числа появились

значительно позже натуральных чисел и обыкновенных дробей. Первые сведения об отрицательных числах встречаются у китайских математиков во II в. до н. э. Положительные числа

тогда толковались

как имущество,

а отрицательные – как

долг, недостача.

Герберт Спенсер

« Дороги не те знания, которые

откладываются в мозгу, как жир, дороги

те, которые превращаются в умственные

мышцы».