
Բուրգ Բուրգի հասկացությունը
10-րդ դասարան
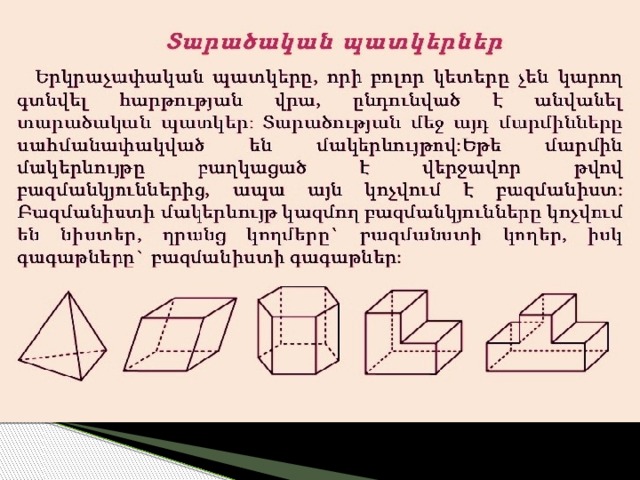



Բազմանիստը,որն առաջանում է բազմանկյան և նրա հարթությանը չպատկանող կետի` այդ բազմանկյան գագաթներին միացումից, կոչվում է Բուրգ


Բուրգի օրինակներ Հին աշխարհի 7 հրաշալիքներից մեկը` Եգիպտական բուրգերը

Եգիպտական բուրգերից ամենամեծը Քեոփսի բուրգն է, որի բարձրությունը 147 մ է:Քարե այդ վիթխարի շինությունը համարվում է աշխարհում բոլոր ժամանակների ձեռակերտ կառույցներից ամենաբարձրը:


Հանրահայտ Լուվրի թանգարանի բուրգանման մուտքը առջևից



Մեքսիկական բրգաձև տուն



Բրգաձև կիսակառույց հյուրանոց,որը կառուցվում է Թեղուտում.
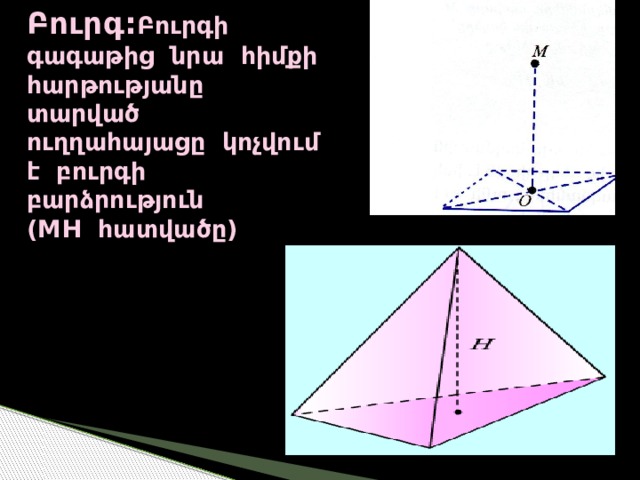
Բուրգ: Բուրգի գագաթից նրա հիմքի հարթությանը տարված ուղղահայացը կոչվում է բուրգի բարձրություն (MH հատվածը)
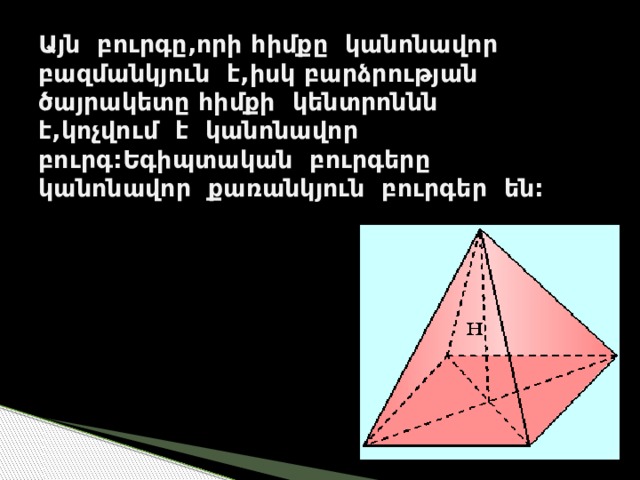
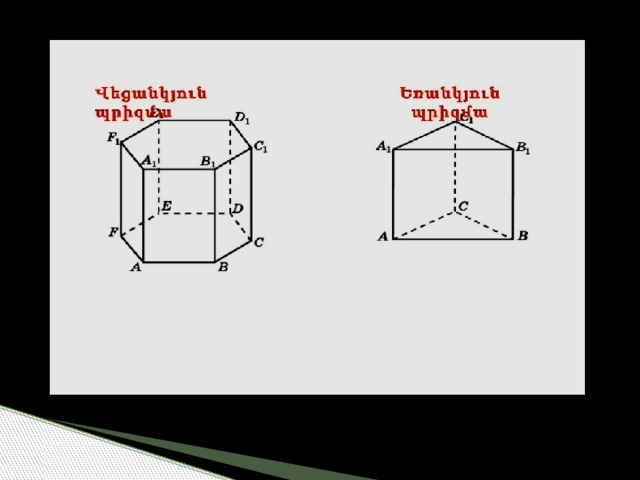
Այն բուրգը,որի հիմքը կանոնավոր բազմանկյուն է,իսկ բարձրության ծայրակետը հիմքի կենտրոննն է,կոչվում է կանոնավոր բուրգ:Եգիպտական բուրգերը կանոնավոր քառանկյուն բուրգեր են:
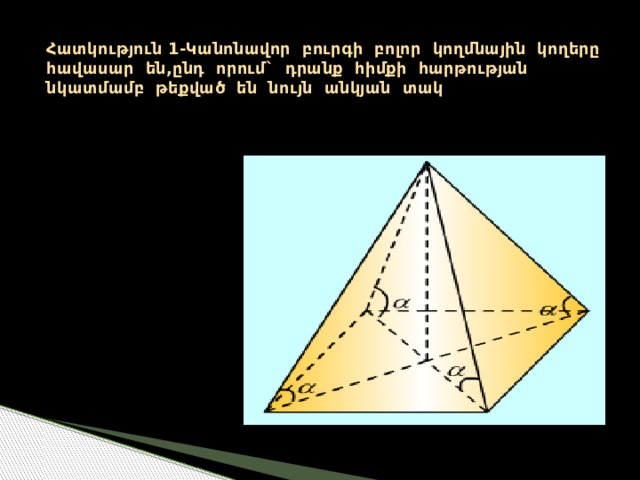
Հատկություն 1-Կանոնավոր բուրգի բոլոր կողմնային կողերը հավասար են,ընդ որում` դրանք հիմքի հարթության նկատմամբ թեքված են նույն անկյան տակ
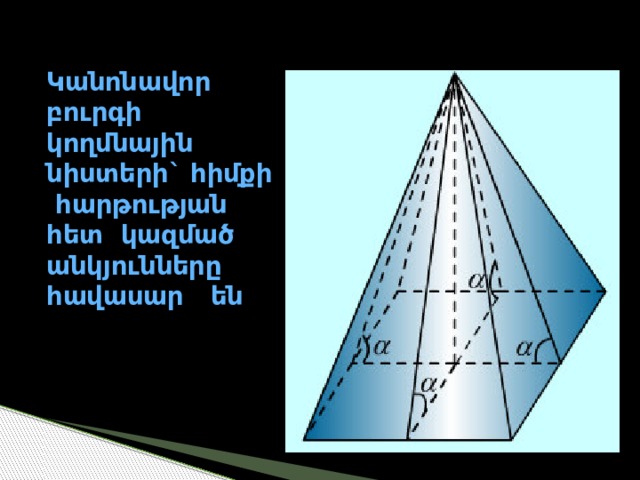
Կանոնավոր բուրգի կողմնային նիստերի` հիմքի հարթության հետ կազմած անկյունները հավասար են
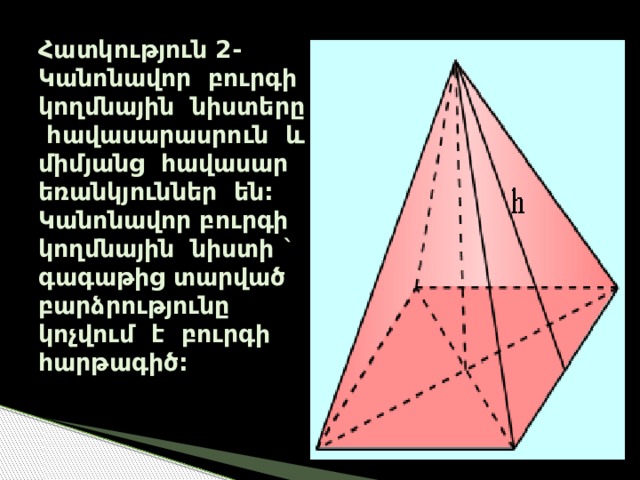
Հատկություն 2-Կանոնավոր բուրգի կողմնային նիստերը հավասարասրուն և միմյանց հավասար եռանկյուններ են: Կանոնավոր բուրգի կողմնային նիստի ` գագաթից տարված բարձրությունը կոչվում է բուրգի հարթագիծ:
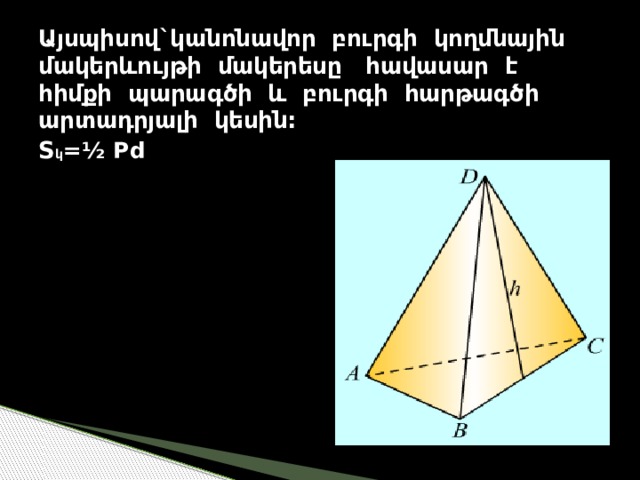
Այսպիսով`կանոնավոր բուրգի կողմնային մակերևույթի մակերեսը հավասար է հիմքի պարագծի և բուրգի հարթագծի արտադրյալի կեսին: S կ = ½ Pd
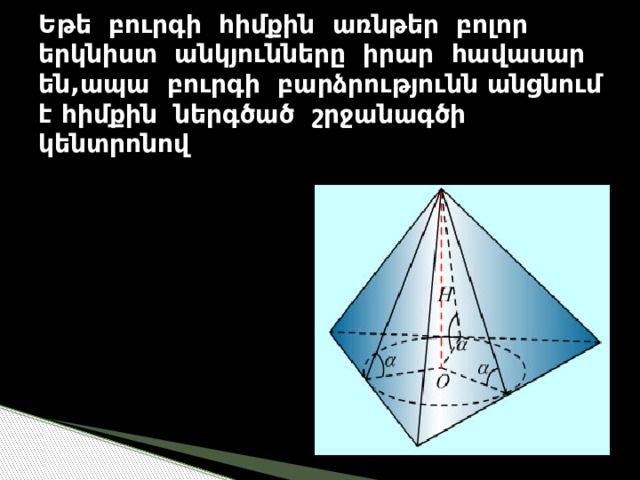
Եթե բուրգի հիմքին առնթեր բոլոր երկնիստ անկյունները իրար հավասար են,ապա բուրգի բարձրությունն անցնում է հիմքին ներգծած շրջանագծի կենտրոնով
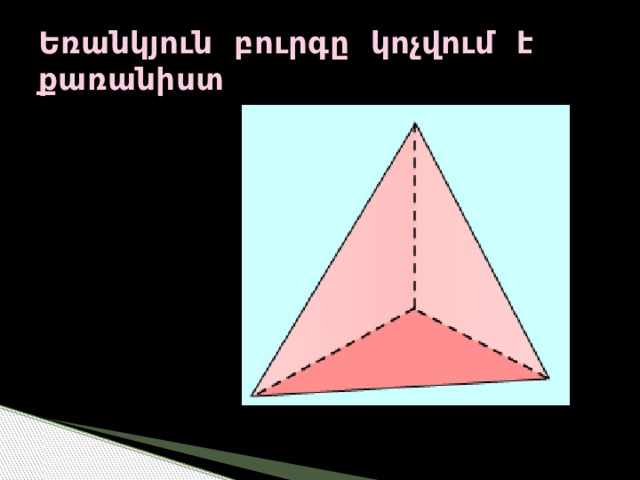
Եռանկյուն բուրգը կոչվում է քառանիստ
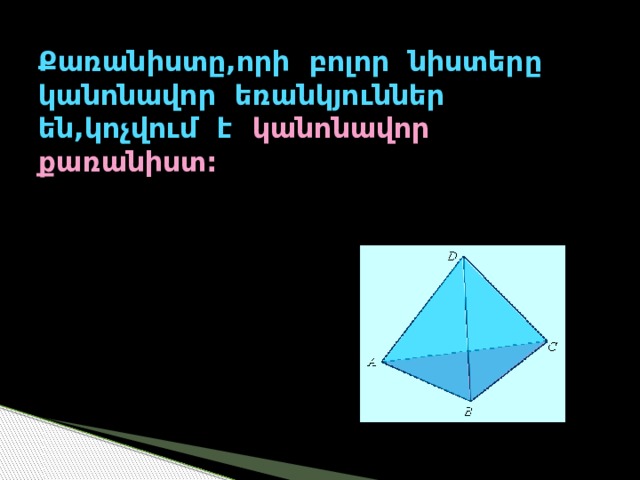
Քառանիստը,որի բոլոր նիստերը կանոնավոր եռանկյուններ են,կոչվում է կանոնավոր քառանիստ:

Բուրգի մակերևույթի մակերես կոչվում է նրա բոլոր նիստերի մակերեսների գումարը,իսկ կողմնային նիստերի մակերեսների գումարը կոչվում է կողմնային մակերևույթի մակերես: Բուրգի մակերևույթի մակերեսը հաշվում են հետևյալ բանաձևով S=S հ +S կ
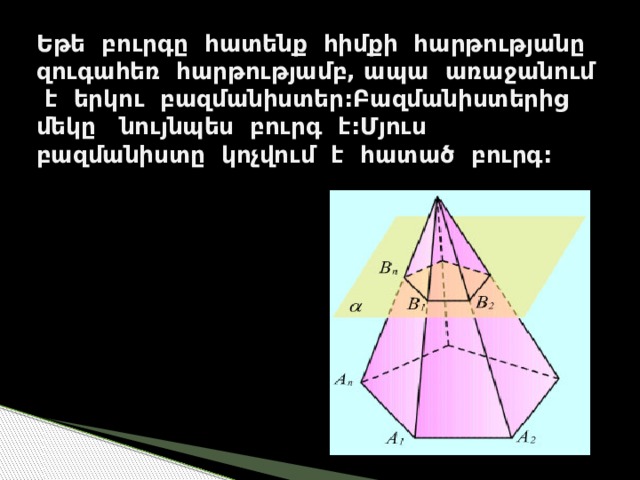
Եթե բուրգը հատենք հիմքի հարթությանը զուգահեռ հարթությամբ, ապա առաջանում է երկու բազմանիստեր:Բազմանիստերից մեկը նույնպես բուրգ է:Մյուս բազմանիստը կոչվում է հատած բուրգ:

Հատած բուրգի կողմնային նիստերը իրենցից ներկայացնում են մի երկրաչափական պատկեր,որը կոչվում է սեղան
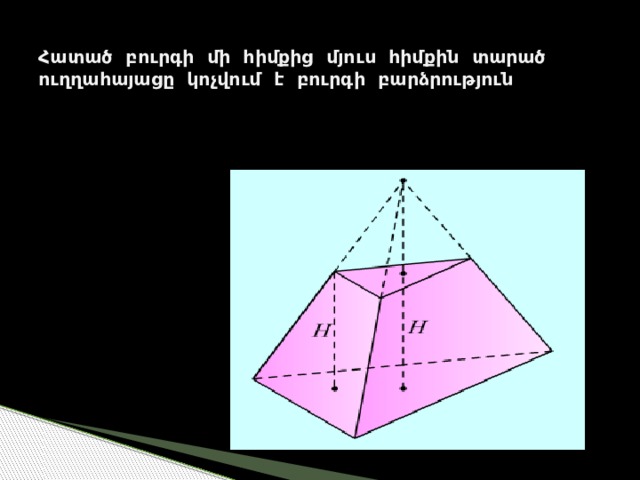
Հատած բուրգի մի հիմքից մյուս հիմքին տարած ուղղահայացը կոչվում է բուրգի բարձրություն
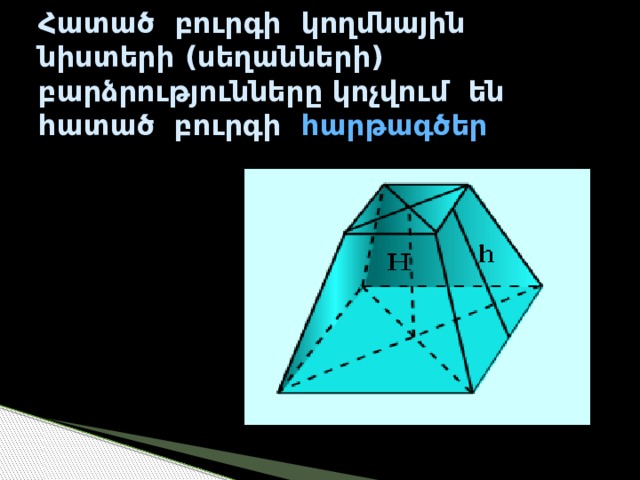
Հատած բուրգի կողմնային նիստերի (սեղանների) բարձրությունները կոչվում են հատած բուրգի հարթագծեր

 Получите свидетельство
Получите свидетельство Вход
Вход











 Բուրգ:Բուրգի հասկացությունը (1.84 MB)
Բուրգ:Բուրգի հասկացությունը (1.84 MB)
 0
0 883
883 0
0 Нравится
0
Нравится
0


