Бином Ньютона
Бином
Задача. Для произвольных вещественных чисел ![]() и натурального
и натурального ![]() выписать разложение выражения
выписать разложение выражения ![]() по степеням
по степеням ![]() и
и ![]() .
.
Из школьного курса алгебры известны эти разложения для малых ![]() :
:
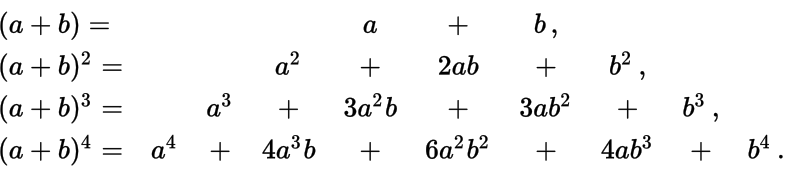
Выражение
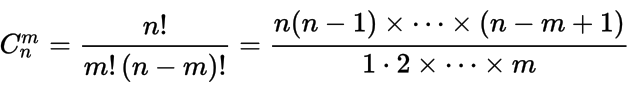
при ![]() и
и ![]() называется биномиальным коэффициентом. В западной литературе принято обозначение
называется биномиальным коэффициентом. В западной литературе принято обозначение ![]() .
.
П
Пример.
![]()
Т
Теорема 1. Для любых натуральных ![]() и
и ![]() справедливы следующие формулы:
справедливы следующие формулы:
![]()
Т
Теорема 2. Имеет место формула бинома Ньютона
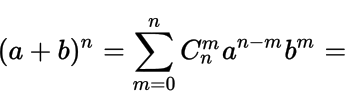
![]()
Доказательство ведется индукцией по ![]() . Для
. Для ![]() формула справедлива. Предположим, что она справедлива для степени
формула справедлива. Предположим, что она справедлива для степени ![]() , докажем ее справедивость для степени
, докажем ее справедивость для степени ![]() , т.е. докажем, что в разложении
, т.е. докажем, что в разложении ![]() по степеням
по степеням ![]() и
и ![]() коэффициент при
коэффициент при ![]() равен .
равен .
Последнее равенство следует из пункта теоремы 1. ♦
Для малых значений показателя ![]() вычисления биномиальных коэффициентов удобно производить по следующей схеме.
вычисления биномиальных коэффициентов удобно производить по следующей схеме.

 Получите свидетельство
Получите свидетельство Вход
Вход


 по степеням x. Коэффициент при x k {\displaystyle x^{k}}
по степеням x. Коэффициент при x k {\displaystyle x^{k}}  обозначается ( n k ) {\displaystyle \textstyle {\binom {n}{k}}}
обозначается ( n k ) {\displaystyle \textstyle {\binom {n}{k}}}  или C n k {\displaystyle \textstyle C_{n}^{k}}
или C n k {\displaystyle \textstyle C_{n}^{k}}  и читается «биномиальный коэффициент из n по k» (или «це из n по k»):
и читается «биномиальный коэффициент из n по k» (или «це из n по k»):
 . Биномиальные коэффициенты могут быть также определены для произвольных n {\displaystyle n}
. Биномиальные коэффициенты могут быть также определены для произвольных n {\displaystyle n} 
 ), и поэтому данное разложение представляет собой конечную сумму ().
), и поэтому данное разложение представляет собой конечную сумму ().








 Бином Ньютона. Расчет биномиальных коэффициентов (115.74 KB)
Бином Ньютона. Расчет биномиальных коэффициентов (115.74 KB)
 0
0 1464
1464 74
74 Нравится
0
Нравится
0


