Конспект урока математики в 9 классе.
Тема урока. «Биквадратные уравнения»
Тип урока. Урок изучения нового материала
Цель урока. Образовательные: познакомить учащихся с новым видом уравнения с одной переменной; изучить и закрепить способ решения биквадратных уравнений; способствовать выработке навыка решения уравнений с помощью введения вспомогательной переменной, проверить усвоение темы на базовом уровне,
Развивающие: развивать и совершенствовать умения применять имеющиеся знания в конкретной ситуации, развивать умение сравнивать, обобщать, правильно формулировать и излагать мысли, развивать память, логическое мышление, интерес к предмету через содержание учебного материала.
Воспитательные: продолжать воспитывать навыки самоконтроля и взаимоконтроля, воспитывать у учащихся аккуратность, культуру общения, воспитывать такие качества характера, как чувство ответственности, настойчивости в достижении цели, умения не растеряться в проблемной ситуации, взаимоуважение.
Задачи. 1. Сформировать интерес к изучению темы и желание применять полученные знания. 2. Сформировать умение видеть математическую задачу в контексте проблемной ситуации.
Оборудование Учебник, наглядный материал.
План урока
Организационный этап
Актуализация опорных знаний
Изучение нового материала
Физминутка
Первичное закрепление нового материала
Итоги урока
Домашнее задание
Ход урока
1. Организационный момент
Приветствие учащихся, мобилизация внимания.
2. Актуализация опорных знаний.
Учитель: Мы продолжаем изучение темы: “ Целые уравнения”. Сегодня на уроке мы познакомимся с новым видом уравнения, приводимого к квадратному, поэтому повторим изученное, вспомнив основные определения, формулы и теоремы. Ответим на вопросы:
1) третья степень числа.
2) с помощью какой теоремы можно найти корни квадратного уравнения либо проверить ответ.
3) формула ![]() b²-4ac
b²-4ac
4) вторая степень числа
5) число, стоящее перед x²
6) если дискриминант равен нулю,то уравнение имеет … корень
7) равенство с переменной
8) если дискриминант больше нуля то уравнение имеет … корня
9)в уравнении ![]() число 5 – это …
число 5 – это …
10) по формуле ![]() находим …
находим …
11)уравнения вида ![]() называют …
называют …
12)уравнения, где левые и правые части являются целыми многочленами называют…
Итак, записываем новую тему



3. Изучение нового материала


Сколько решений может иметь биквадратное уравнение?
От чего зависит число решений биквадратного уравнения?

4.Физминутка
Первичное закрепление нового материала
Решить уравнения:
![]()
![]()
![]()
![]()

6.Итоги урока


Выставление оценок.
7.Домашнее задание
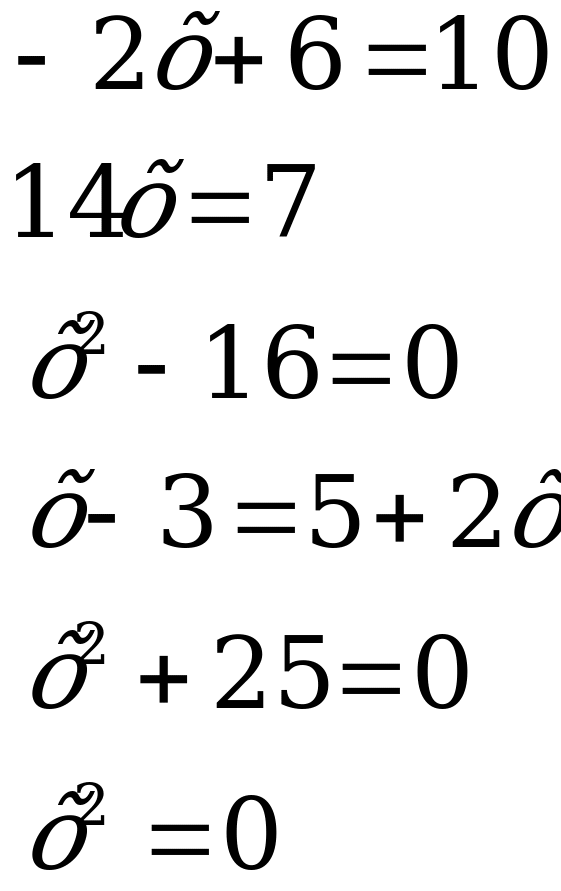

 Получите свидетельство
Получите свидетельство Вход
Вход




![В решение уравнений третьей и четвёртой степеней большой вклад внесли итальянские математики XVI века. C пицион Ферро [1465-1526] и его ученик Фиоре. Раффаэле Бомбелли Николо Тарталья Джероламо Кардано [ ок.1530-1572 ] [ ок.1499-1557 ] [1501-1576]](https://fsd.videouroki.net/html/2025/01/19/v_678cfb71434af/img_v99806955_1_2.jpg)



















 Биквадратные уравнения (8.34 MB)
Биквадратные уравнения (8.34 MB)
 0
0 395
395 13
13 Нравится
0
Нравится
0


