Цели урока:
Образовательные: систематизировать и обобщить материал по данной теме.
Развивающие: продолжить работу по формированию у учащихся умений проводить обоснования, делать выводы, выделять главное в изучаемом материале.
Воспитательные: прививать навыки самостоятельности, активизировать наблюдательность.

Равенство, содержащее переменные, называется уравнением.
Корнем уравнения с одной переменной называется такое значение переменной, при котором уравнение превращается в верное равенство.
Решить уравнение –значит, найти все его корни или доказать, что оно корней не имеет.
КВАДРАТНОЕ УРАВНЕНИЕ
Квадратным называют алгебраическое уравнение 2-ой степени, т.е. уравнение вида ax²+bx+c=0, где а≠0. (1)
Выражение D=b²-4ac называют дискриминантом квадратичного трехчлена ax²+bx+c. При этом если D>0, то корни действительные и различные, при D=0 корни совпадают (говорят, что уравнение имеет корень кратности два), при D<0 корни комплексные (комплексно сопряжённые).
Эти соотношения называют теоремой Виета, по имени французского математика Ф. Виета (1540÷1603).
Особенно удобна эта теорема для приведенного квадратного уравнения. Формула корней квадратного уравнения «переоткрывалась» неоднократно.
Один из первых, дошедших до наших дней выводов этой формулы принадлежит индийскому математику Брахмагупте (около 598г.). Среднеазиатский ученый ал-Хорезми (IX в.) в трактате «Китаб аль-джебр валь -мукабала» получил эту формулу методом выделения полного квадрата с помощью геометрической иллюстрации.
К квадратным уравнениям сводятся многие уравнения путем замены переменной.
Приведём некоторые примеры.
1. Биквадратное уравнение сводится к квадратному заменой переменной
2. Уравнение заменой сводится к квадратному уравнению ,корни которого равны . Из двух уравнений и действительные решения имеет только первое : .
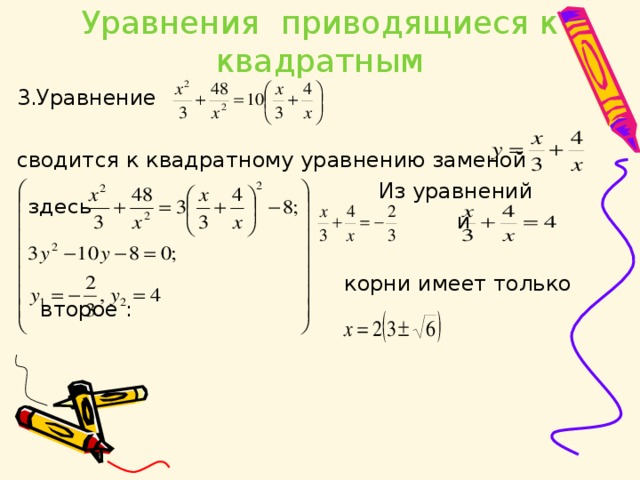
3. Уравнения сводятся к квадратным заменам соответственно и .
4. Уравнение сводится к квадратному уравнению заменой
Вообще, замена - одна из наиболее часто встречающихся.
Например ,с помощью такой замены к квадратному уравнению (после деления обеих частей уравнения на ) сводится уравнение вида . (2)
Уравнение (2) обычно называют возвратным или обобщенно-симметрическим.
Однородные уравнения и сводятся к квадратным уравнениям относительно заменами соответственно и после деления обеих частей первого уравнения на ,второго - на .
Для второго уравнения предварительно проверяется, удовлетворяют ли уравнению те значения , для которых .
6. Уравнение «симметричное» относительно ,сводится к биквадратному уравнению заменой ; аналогично уравнение , «симметричное» относительно ,сводится к биквадратному уравнению заменой.

 Получите свидетельство
Получите свидетельство Вход
Вход








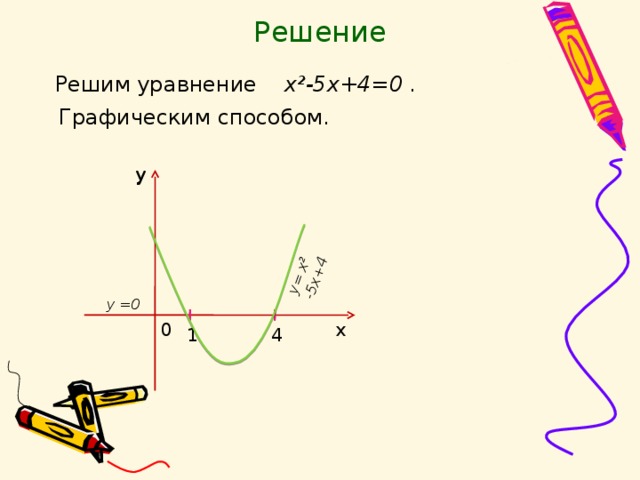










 0. откуда или и Решая полученные уравнения, находим " width="640"
0. откуда или и Решая полученные уравнения, находим " width="640"













 Классификация квадратных уравнений и уравнений, приводимых к ним (1.48 MB)
Классификация квадратных уравнений и уравнений, приводимых к ним (1.48 MB)
 0
0 1060
1060 19
19 Нравится
0
Нравится
0


