31
ЧИСЛА ФИБОНАЧЧИ. ЗОЛОТОЕ СЕЧЕНИЕ.
Работу выполнила:
СОДЕРЖАНИЕ
-
Вступление стр. 4 – 6
-
Раздел1 Числа Фибоначчи стр. 7 – 10
Подразделы
-
Фибоначчи стр. 7
-
Ряд чисел Фибоначчи стр. 7 – 8
-
Задача о кроликах стр. 8
-
Свойства чисел Фибоначчи стр. 8 – 9
-
Различные соотношения чисел Фибоначчи стр. 9 – 10
-
Спираль Фибоначчи стр. 10
3. Раздел2 Золотое сечение стр. 11 – 12
Подразделы
-
Понятие «Золотое сечение» стр. 11
-
Коэффициент золотого сечения стр. 11
-
Геометрическое изображение золотой пропорции стр. 11 – 12
4.Раздел3 Золотое сечение, числа и спираль Фибоначчи в окружающем нас мире стр. 13 – 23
Подразделы
3.1. В природе стр. 13 – 14
3.2. В человеке стр. 14 – 15
3.3. В скульптуре стр. 15 – 17
Пункты
3.3.1. Статуя «Дорифор» стр. 15 – 16
3.3.2. Статуя Аполлона Бельведерского стр. 16
3.3.3. Статуя Зевса Олимпийского и Афины Парфенон стр. 16
3.3.4. Статуя Венера Милосская стр. 16 – 17
3.4. В живописи стр. 17 – 19
Пункты
3.4.1. Картина Леонардо да Винчи «Мона Лиза» стр. 17 – 18
3.4.2. Картина Рафаэля «Избиение младенцев» стр. 18
3.4.3. Картина И. И. Шишкина «Сосновая роща» стр. 18 – 19
3.5. В музыке стр. 19 – 20
3.6. В поэзии и прозе стр. 20 – 22
3.7. В архитектуре стр. 22 – 23
Пункты
3.7.1. Парфенон стр. 22
3.7.2. Голицынская больница (Первая клиническая больница имени Н.И. Пирогова) стр. 22 – 23
3.7.3. Пирамида Хеопса стр. 23
3.7.4. Дом Пашкова стр. 23
5. Вывод стр. 24
6. Список использованной литературы стр. 25
7. Приложение стр. 26 – 27
ВСТУПЛЕНИЕ
С давних пор человек стремится окружать себя красивыми вещами. Уже предметы обихода жителей древности, которые, казалось бы, преследовали чисто утилитарную цель – служить хранилищем воды, оружием на охоте и т.д., демонстрируют стремление человека к красоте. На определенном этапе своего развития человек начал задаваться вопросом: почему тот или иной предмет является красивым и что является основой прекрасного? Уже в Древней Греции изучение сущности красоты, прекрасного, сформировалось в самостоятельную ветвь науки – эстетику, которая у античных философов была неотделима от космологии. Тогда же родилось представление о том, что основой прекрасного является гармония.
Красота и гармония стали важнейшими категориями познания, в определенной степени даже его целью, ибо в конечном итоге художник ищет истину в красоте, а ученый – красоту в истине.
Красота скульптуры, красота храма, красота картины, симфонии, поэмы,… что между ними общего? Разве можно сравнить красоту храма с красотой ноктюрна? Оказывается можно, если будут найдены единые критерии прекрасного, если будут открыты общие формулы красоты, объединяющие понятие прекрасного самых различных объектов – от цветка ромашки до красоты обнаженного человеческого тела.
Известный итальянский теоретик архитектуры Леон-Баттиста Альберти, написавший много книг о зодчестве, говорил о гармонии следующее:
«Есть нечто большее, слагающееся из сочетания и связи трех вещей (числа, ограничения и размещения), нечто, чем чудесно озаряется весь лик красоты. Это мы называем гармонией, которая, без сомнения, источник всякой прелести и красоты. Ведь назначение и цель гармонии – упорядочить части, вообще говоря, различные по природе, неким совершенным соотношениям так, чтобы они одна другой соответствовали, создавая красоту… Она охватывает всю жизнь человеческую, пронизывает всю природу вещей, ибо все, что производит природа, все это соизмеряется законом гармонии. И нет у природы большей заботы, чем та, чтобы произведенное ею было совершенным. Этого никак не достичь без гармонии, ибо без нее распадается высшее согласие частей».
В Большой Советской Энциклопедии дается следующее определение понятия «гармония».
«Гармония – соразмерность частей и целого, слияние различных компонентов объекта в единое органическое целое. В гармонии получают внешние выявление внутренняя упорядоченность и мера бытия».
«Формула красоты» уже известна немало. Уже давно в своих творения люди предпочитают правильные геометрические формы – квадрат, круг, равнобедренный треугольник, пирамиду и т. д. в пропорциях сооружений отдаются предпочтения целочисленным соотношениям.
Из многих пропорций, которыми издавна пользовался человек при создании гармонических произведений, существует одна, единственная и неповторимая, обладающая уникальными свойствами. Эту пропорцию называли по разному – «золотой», «божественной», «золотым сечением», «золотым числом», «золотой серединой».
Загадка притягательной силы золотого сечения давно волнует человечество. «Эта наша пропорция, высокочтимый герцог, достойна такой привилегии и такого превосходства, какие только можно высказать по поводу ее безграничных возможностей» – этими словами начиналась одна из главных книг монаха ордена францисканцев Луки Пачоли « О божественной пропорции». «Золотое сечение» назвал эту пропорцию друг Пачоли великий итальянский живописец, скульптор, архитектор, ученый и инженер Леонардо до Винчи.
Что же того замечательного скрыто в этой пропорции, что она занимает умы людей много веков? В золотой пропорции кроются удивительные математические закономерности, но самое главное – считается, что формы, основанные на золотом сечении, наиболее привлекательны с эстетической точки зрения и поэтому с давних пор используются художниками, дизайнерами, архитекторами.
РАЗДЕЛ 1
Ряд чисел Фибоначчи
1.1. Фибоначчи
Фибоначчи (ок. 1180 – 1250) – итальянский математик. Леонардо Фибоначчи иногда называют Леонардо Пизанский, так как он жил в городе Пизе. А «Фибоначчи» означает, что он был сыном Боначчи. Он был большим знатоком всевозможных соотношений между числами и весьма искусным вычислителем. По обычаям того времени Леонардо Фибоначчи участвовал в математических турнирах, на которых необходимо было быстро решать трудные математические задачи. Его способности поражали всех. В 1202 году Фибоначчи издал книгу на латинском языке, которая называлась «Книга об абаке». В этой книге содержались все знания того времени по арифметике и алгебре. Это была одна из первых книг в Европе, учившая употреблять десятичную систему счисления. В своем труде Фибоначчи обобщил знания математиков стран Востока, Древней Греции и Европы. «Книга абака» способствовала распространению алгебраических знаний в Италии, Германии, Франции и других странах, эта книга более двух столетий была основным источником математических знаний в Европе. Известна и другая книга Фибоначчи «Практическая геометрия». В этой книге впервые встречается формула для вычисления объема усеченной пирамиды, но дается она в словесной форме. В этой книге еще много полезных и интересных фактов, в том числе и доказательство теоремы Пифагора, которое очень близко к доказательству, приводимому в школьных учебниках.
1.2. Ряд чисел Фибоначчи
Ряд Фибоначчи – ряд чисел: 1, 1, 2, 3, 5, 8, 13, 21,… . правило образования членов этого ряда следующие: первые два числа – единицы, а затем каждый последующий член получается путем сложения двух непосредственно ему предшествующих. Например: 2 = 1 + 1; 3 = 1 + 2; 5 = 2 + 3; 8 = 3 + 5; 13 = 5 + 8; 21 = 8 + 13 и т. д.
1.3. Задача о кроликах
Сколько пар кроликов в один год рождается от одной пары? Если некто поместит пару кроликов в неком месте, огражденном со всех сторон стеной притом, что порода кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения.
Решение. Так как первая пара кроликов в первом месяце дает потомство, удвой, и в этом месяце окажутся 2 пары; из них одна пара, а именно первая, рождает и в следующем месяце, так что во втором месяце оказывается 3 пары; из них в следующем месяце 2 пары будут давать потомство, так что в третьем месяце рождаются еще две пары кроликов, и число пар кроликов в этом месяце достигнет 5, из них в этом же месяце будут давать потомство 3 пары, и число пар кроликов в четвертом месяце достигнет 8; из них 5 пар произведут другие 5 пар, которые, сложенные с 8 парами, дадут в пятом месяце 13 пар; из них 5 пар рожденных в этом месяце, не дают в том же месяце потомства, так что в шестом месяце оказывается 21 пара; сложенные с 13 парами, которые родятся в седьмом месяце, они дают 34 пары; сложенные с 21 парой, рожденной в восьмом месяце, они дают в этом месяце 55 пар; сложенные с 34 парами, рожденными в девятом месяце, они дают 89 пар; сложенные вновь с 55 парами, которые рождаются в десятом месяце, они дают в этом месяце 144 пары; снова сложенные с 89 парами, которые рождаются в одиннадцатом месяце, они дают в этом месяце 233 пары, сложенные вновь с 144 парами, рожденными в последнем месяце, они дают 377 пар.
Ответ: 377 пар произвела первая пара в данном месте к концу одного года.
1.4. Свойства чисел ряда Фибоначчи
1.4.1. Любой член ряда можно найти по формуле ![]() , где
, где ![]() ;
; ![]() .
.
1.4.2. Любая пара соседних чисел ряда удовлетворяет одному из уравнений ![]() , причем
, причем ![]() , а
, а ![]() .
.
1.4.3. Сумма первых n членов находится по формуле: ![]() .
.
1.4.4. Сумма квадратов чисел ряда выражается через произведение двух соседних членов того же ряда, т.е. ![]() .
.
1.4.5. Квадрат каждого члена ряда, уменьшенный на произведение предшествующего и последующего членов, дает попеременно то +1, то -1. Например: ![]() ;
; ![]() ;
; ![]() и т.д.
и т.д.
1.4.6. В ряду Фибоначчи каждое третье число четное, каждое четвертое делится на 3, каждое пятое делится на 5, каждое пятнадцатое делится на 10.
1.4.7. Невозможно построить треугольник, сторонами которого являются числа ряд Фибоначчи, при условии, что каждое число ряда не может быть использовано дважды.
1.4.8. Если взять любые четыре последовательных числа ряда Фибоначчи и рассмотреть произведение крайних членов и удвоенное произведение средних как длины катетов прямоугольного треугольника, то длиной его гипотенузы будет один из членов этого ряда, т.е. ![]()
1.5. Различные соотношения чисел Фибоначчи
1.5.1. Отношения каждого числа к последующему более и более стремится к 0.618 по увеличению порядкового номера (данное число называется числом Фибоначчи, ![]() (фи)). А отношение каждого числа к предыдущему стремится к 1.618 (обратному к 0.618).
(фи)). А отношение каждого числа к предыдущему стремится к 1.618 (обратному к 0.618).
1.5.2. При делении каждого числа на следующее за ним через одно получается число 0.382, а наоборот – соответственно 2.618.
1.5.3. Подбирая, таким образом, соотношения, получаем основной набор фибоначчиевских коэффициентов: … 4.235, 2.618, 1.618, 0.382, 0.236.
1.6. Спираль Фибоначчи
Если построить прямоугольник со сторонами 21см и 34см (золотой прямоугольник), а затем отрезов от него квадрат, сторона которого равна меньшей стороне (стороне = 21см) прямоугольника, мы снова получим золотой прямоугольник меньших размеров. Мы будем отрезать квадраты до тех пор, пока не получим квадраты со сторонами 1см.
Соединив диагонали квадратов, мы получим спираль Фибоначчи рис.1.1.
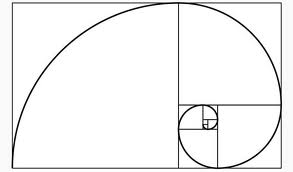
Рис.1.1 Спираль Фибоначчи
РАЗДЕЛ 2
Золотое сечение
2.1. Понятие «золотое сечение»
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему рис.2.2, a : c = b : с или с : b = b : a.
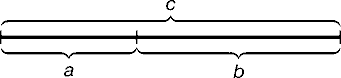 Рис.2.2
Рис.2.2
2.2. Коэффициент золотого сечения.
Ряд Фибоначчи тесно связан с золотым сечением. Так как число 0.618 представляет собой постоянный коэффициент золотого сечения, т.е. любой отрезок делится таким образом, что отношение между его меньшей и большей частью равно соотношению между большей частью и всем отрезком и равно 0.618. Таким образом, число ![]() = 0.618, известно еще как золотой коэффициент или золотая середина.
= 0.618, известно еще как золотой коэффициент или золотая середина.
2.3. Геометрическое изображение золотой пропорции рис.2.3
Практическое знакомство с золотым сечением начинают с деления отрезка АВ прямой в золотой пропорции с помощью циркуля и линейки. Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции. Отрезки золотой пропорции выражаются иррациональной бесконечной дробью AE = 0,618..., если АВ принять за единицу, ВЕ = 0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.
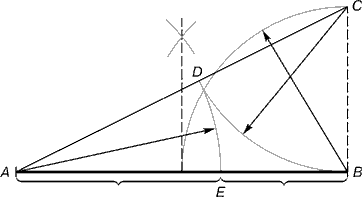 Рис.2.3
Рис.2.3
РАЗДЕЛ 3
Золотое сечение, числа и спираль Фибоначчи в окружающем нас мире
3.1.В природе
3.3.1. Многие растения растут по спирали Фибоначчи. Каждый новый стебель вырастает с внутренней стороны предыдущего, и растение как бы закручивается. Спирали роста можно обнаружить у сельдерея, у всех кактусов, у пальм, в сосновых шишках, в цветах маргаритки или подсолнуха и у многих других растений. Например: семена шишки образуют сразу два множества спиралей: 8 спиралей по 8 семян (синие) идут по часовой стрелке, а 13 спиралей по 5 семян (красные) идут против часовой стрелки рис.3.4
 Рис.3.4 Спирали шишки
Рис.3.4 Спирали шишки
3.3.2.Для всего животного мира характерны симметрия форм и наличие парных органов, членение на три части тела, членение конечностей на 3 и 5 частей, а брюшка – на 3.
3.3.3.Многие насекомые в горизонтальном разрезе имеют простые асимметричные формы, основанные на золотом сечении. Например: у многих бабочек соотношение размеров грудной и брюшной части тела отвечает золотой пропорции. Сложив крылья, ночная бабочка образует правильный равносторонний треугольник. Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2, 3, 5, 8; очень совершенна форма стрекозы, которая создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.
3.3.4.Строение форм представителей более высокого уровня животного мира подчиняется закону Фибоначчи. Например: у черепахи в панцире имеется 13 сросшихся пластин, из них 5 пластин в центре, а 8 по краям, на лапках 5 пальцев, а позвоночник содержит 34 позвонка; панцирь современных крабов состоит из 13 пластин, а древних содержал 8 пластин.
3.3.5. У живородящей ящерицы четко прослеживается золотая пропорция.
Расстояние от головы до задних конечностей так относится к расстоянию от задних конечностей до кончика хвоста как расстояние от задних конечностей до кончика хвоста ко всей длине ящерицы рис3.5.
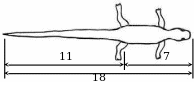 Рис.3.5
Рис.3.5
3.2. В человеке
В 1855г. немецкий исследователь золотого сечения профессор Цейзиг опубликовал свой труд «Эстетические исследования». Он измерил около 2 тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон.
Если принять центром человеческого тела точку пупа, а расстояние между ступней человека и точкой пупа за единицу измерения, то рост человека эквивалентен числу 1.618. Расстояние от уровня плеча до макушки головы и размера головы равно 0.618. Расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 0.618. Расстояние точки пупа и от коленей до ступней равно 0.618. расстояние от кончика подбородка до кончика верхней губы до ноздрей равно 0.618. Расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 0.618. собственно точное наличие золотой пропорции в лице человека и есть идеал красоты для человеческого взора. Если внимательно посмотреть на указательный палец, то вы сразу же найдете в нем формулу золотого сечения. Каждый палец нашей руки состоит из трех фаланг. Сумма двух первых фаланг пальца в соотношении со всей длиной пальца и дает число золотого сечения (за исключением большого пальца). Кроме того, соотношения между средним пальцем и мизинцем также равно числу золотого сечения. У человека 2 руки, пальцы на каждой руке состоят из трех фаланг (за исключением большого пальца). На каждой руке имеется пять пальцев, т. е. всего 10, но за исключением двух двухфаланговых больших пальцев только 8 пальцев создано по принципу золотого сечения. Все эти цифры 2,3, 5 и 8 есть числа последовательности Фибоначчи.
3.3. В скульптуре
Известно, что древние скульпторы знали и использовали золотую пропорцию как критерий гармонии, канон красоты, корни которой лежат в пропорциях человеческого тела. Эталонами красоты человеческого тела, образцами гармонического телосложения издавна и по праву считаются великие творения греческих скульпторов. В создании своих творений мастера использовали принцип золотой пропорции. Например:
3.3.1. Одним из высших достижений классического греческого искусства может служить статуя «Дорифор» рис.3.6, изваянная Поликлетом (V век до н. э.). Статуя представляет собой фигуру юноши и выражает единство прекрасного и доблестного, лежавших в основе греческих принципов искусства. Эта статуя считается примером для анализа пропорций идеального человеческого тела, установленных античными греческими скульпторами, и напрямую связана с золотым сечением ![]() = 0.618.
= 0.618.
 Рис.3.6 Статуя «Дорифор»
Рис.3.6 Статуя «Дорифор»
3.3.2. Знаменитая статуя Аполлона Бельведерского рис.3.7 состоит из частей, делящихся по золотым отношениям.
 Рис.3.7 статуя Аполлона Бельведерского
Рис.3.7 статуя Аполлона Бельведерского
3.3.3. Великий древнегреческий скульптор Фидий часто использовал золотое сечение в своих произведениях. Самыми знаменитыми из них были статуя Зевса Олимпийского рис.3.8 и Афины Парфенон рис.3.9
 Рис.3.8
Рис.3.8  Рис.3.9
Рис.3.9
Статуя Зевса Олимпийского Статуя Афины Парфенон
3.3.4. Венера Милосская рис.3.10, статуя богини любви Афродиты и эталон женской красоты, является одним из лучших памятников греческого скульптурного искусства. Она также построена на пропорциях золотого сечения.
 Рис.3.10 Статуя Венера Милосская
Рис.3.10 Статуя Венера Милосская
3.4. В живописи
3.4.1.Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: “Пусть никто, не будучи математиком, не дерзнет читать мои труды”. Он снискал славу непревзойденного художника, великого ученого, гения, предвосхитившего многие изобретения, которые не были осуществлены вплоть до XX в. Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится “обо всем на свете”. Он писал справа налево неразборчивым почерком и левой рукой. Это самый известный из существующих образец зеркального письма. Портрет Моны Лизы (Джоконды) рис.3.11 долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Зрачок левого глаза, через который проходит вертикальная ось полотна, находится на пересечении двух биссектрис верхнего золотого треугольника, которые с одной стороны, делят пополам углы при основании золотого треугольника, а с другой стороны, в точках пересечения с бедрами треугольника делят их в пропорции золотого сечения. Таким образом, Леонардо да Винчи использовал в своей картине не только принцип симметрии, но и золотое сечение.
 Рис.3.11
Рис.3.11
3.4.2. В картине Рафаэля «Избиение младенцев» рис.3.12 просматривается другой элемент золотой пропорции – золотая спираль. На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции – точки, где пальцы воина сомкнулись вокруг лодыжки ребенка – вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза.
 Рис.3.12 Картина Рафаэля
Рис.3.12 Картина Рафаэля
«Избиение младенцев»
3.4.3. На знаменитой картине И. И. Шишкина «Сосновая роща» рис.3.13 с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны - освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали. Слева от главной сосны находится множество сосен - при желании можно с успехом продолжить деление картины по золотому сечению и дальше.
Наличие в картине ярких вертикалей и горизонталей, делящих ее в отношении золотого сечения, придает ей характер уравновешенности и спокойствия, в соответствии с замыслом художника.
 Рис.3.13 картина И. И. Шишкина
Рис.3.13 картина И. И. Шишкина
«Сосновая роща»
3.5. В музыке
В композиции многих музыкальных произведений отмечается наличие некоторого «кульминационного взлета», высшей точки, причем такое построение характерно не только для произведения в целом, но и для его отдельных частей. Такая высшая точка крайне редко расположена в центре произведения или его композиционной части, обычно она смещена, ассиметрична.
3.5.1. Изучая восьмитактные мелодии Бетховена, Шопена, Скрябина, советский музыковед Л. Мазель установил, что во многих из них вершина, или высшая точка, приходится на сильную долю шестого такта или на мелкую последнюю долю пятого такта, т.е. находится в точке золотого сечения. По мнению Л. Мазеля, число подобных восьмитактов, где подъем мелодии, занимает пять тактов, а последующий спуск – три, необычайно велико. Их можно без труда найти почти у каждого автора, сочиняющего музыку в гармоническом стиле. Очевидно, такое расположение кульминационных моментов музыкальной мелодии является важным элементом ее гармонической композиции, придающим художественную выразительность и эстетическую эмоциональность мелодии.
3.5.2. Наиболее обширное исследование проявлений золотого сечения в музыке было предпринято Л. Сабанеевым. Им было изучено две тысячи произведений различных композиторов. По его мнению, временное протяжение музыкального произведения делится «некоторыми вехами», которые выделяются при восприятии музыки и облегчают созерцание формы целого. Все эти музыкальные вехи делят целое на части, как правило, по закону золотого сечения. По наблюдениям Л. Сабанеева, в музыкальных произведениях различных композиторов обычно констатирует не одно золотое сечение, а целая серия подобных сечений. Каждое такое сечение отражает свое музыкальное событие, качественный скачок в развитии музыкальной темы. В изученных 1770 сочинениях 42 композиторов наблюдалось 3275 золотых сечений. Количество произведений, в которых наблюдалось хотя бы одно золотое сечение, составило 1338. наибольшее количество музыкальных произведений, в которых имеется золотое сечение, у Аренского (95%), Бетховена (97%), Гайдна (97%), Моцарта (91%), Скрябина (90%), Шопена (92%), Шуберта (91%).
3.6. В поэзии и прозе.
Если музыка – гармоническое упорядочение звуков, то поэзия – гармоническое упорядочение речи. Золотое сечение в поэзии в первую очередь проявляется как наличие определенного момента стихотворения (кульминации, смыслового перелома, главной мысли произведения) в строке, приходящейся в точку деления общего числа строк стихотворения в золотой пропорции.
Произведения А.С. Пушкина – образец наиболее выдающихся творений русской культуры, образец высочайшего уровня гармонии.
Рассмотрим его знаменитую «Вакхическую песню». В стихотворении всего 16 строк. Ставшая крылатой десятая строка стихотворения «Да здравствуют музы, да здравствует разум!» концентрирует в себе мысль стихотворения. Где расположена эта строка? Точно на линии золотого сечения (16 : 10 = 1.6).
В качестве примера прозаического произведения исследователями была рассмотрена композиция «Пиковой дамы» А.С. Пушкина. В повести 853 строки. Главным моментом является сцена в спальне графини, куда проник Герман в надежде узнать тайну трех карт, сцена, которая оканчивается смертью графини. Следовательно, кульминационный момент повести – это смерть графини. Ему отвечает 536-я строка. Эта строка расположена в повести почти точно в месте золотого сечения, т.к. 853 : 536 = 1.6. повесть состоит из шести глав. В первой главе золотому сечению отвечает 68 строчка, всего в главе 110 строк. Но ведь это узловая точка повествования, в ней переломный момент всей главы: откроет ли граф Сен-жерман свою тайну графине! Вторая глава повести содержит 219 строк. Золотое сечение здесь приходится на 135 строку. Но ведь это кульминационный момент главы: Лиза увидела в окне стоящего на улице Германа! Отсюда начался для нее новый отчет времени, начались события, определившие всю ее дальнейшую судьбу. А. С. Пушкин совершенно точно определил это место во второй главе: ведь 219 : 135 = 1.62. Третья глава повести описывает усилия Германа попасть в дом старой графини, выведать у нее тайну трех карт. Это место начинает новый отсчет времени для Германа. Эта ситуация приходится на 131 строку третьей главы, а всего в ней 212 строк. Разделив 212 на 131, мы получим точно золотую пропорцию 1.618. в четвертой главе размером 113 строк золотая пропорция приходится на 70 строку. Это также переломный, трагический момент в жизни Лизы. В пятой главе описано посещение Германа похорон графини. 46 строка пятой главы разделила повествование на две части: первая – похороны графини, вторая – сон Германа. Эта 46 строка также отвечает золотой пропорции, ведь всего в этой главе 75 строк (75 : 46 = 1.63) в последней главе повести золотая пропорция приходится на 77 строчку, которая завершает описание первого дня игры Германа в карты и первого его выигрыша. Как видим, и в композиции последней главы повести присутствует золотая пропорция.
Золотая пропорция присутствует и в композиции других произведений Пушкина.
В рассказе «Станционный смотритель» 377 строк. Кульминационный момент рассказа – это известие о том, что дочь смотрителя уехала с гусаром. Этот момент отражен во фразе, которая является 214 строкой. Здесь почти точное соответствие золотой пропорции ( 377 : 214 = 1.76)
В маленьком рассказе «гробовщик» всего 229 строк. Со 139 строки начинается описание страшного сна гробовщика. И здесь переломный момент рассказа приходится почти точно на золотую пропорцию (226 : 139 = 1.6)
Совпадение кульминационных моментов в произведениях А.С. Пушкина с золотой пропорцией удивительно близкое. Чувство гармонии у него было развито необыкновенно, что объективно подтверждает гениальность великого поэта и писателя.
Аналогичные выводы были получены и при анализе поэтических и прозаических произведений авторов, живших в различные эпохи.
3.7. В архитектуре
3.7.1. Одним из красивейших произведений древнегреческой архитектуры является Парфенон рис3.– храм богини Афины, возведенный в 447 – 438 гг.до н.э. Иктином и Каллистратом в ознаменование победы над персами. Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Отношение высоты здания к его длине равно 0,618.
3.7.2. Известный русский архитектор М. Казаков в своем творчестве широко использовал «золотое сечение». Его талант был многогранным, но в большей степени он раскрылся в многочисленных осуществленных проектах жилых домов и усадеб. Например, «золотое сечение» можно обнаружить в архитектуре здания сената в Кремле. По проекту М. Казакова в Москве была построена Голицынская больница (Первая клиническая больница имени Н.И. Пирогова).
3.7.3.пропорции пирамиды Хеопса, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.
3.7.4. Один из архитектурных шедевр Москвы – дом Пашкова – является одним из наиболее совершенных произведений архитектуры В. Баженова. Прекрасное творение В. Баженова прочно вошло в ансамбль центра современной Москвы, обогатило его. Наружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 г. При восстановлении здание приобрело более массивные формы. Многие высказывания зодчего заслуживают внимание и в наши дни. О своем любимом искусстве В. Баженов говорил: «Архитектура – главнейшие имеет три предмета: красоту, спокойность и прочность здания... К достижению сего служит руководством знание пропорции, перспектива, механика или вообще физика, а всем им общим вождем является рассудок».
ВЫВОД
Золотое сечение мы находим всюду: в архитектуре, музыке, живописи, литературе, прикладных искусствах. На точку золотого сечения обычно приходится кульминация или главная мысль поэтического, драматургического или музыкального произведения. Золотое сечение мы находим всегда: в цивилизациях, отдельных друг от друга тысячелетиями, в усыпальнице Хеопса в Древнем Египте и в храме Парфенон в Древней Греции. Золотое сечение мы обнаруживаем и в музыкальных произведениях от Баха до Бартона, и в поэтических произведениях А.С. Пушкина до Вознесенского, и в живописи от Андрея Рублева до Сальвадора Дали. Наука и искусство – два высших начала культуры. Их высшая цель – быть дополняющими друг другу. Из многих искусств, допускающих математическое описание, мы рассмотрели только пять : скульптура, живопись, музыка, литература и архитектура. Красота математик среди наук недосягаема, а красота является одним из связующих звеньев природы, науки и искусства.
Чтобы исследовать сколько, учащихся моего класса имеют гармоничность в строении (телосложении), мною были произведены некоторые измерения (из подраздела 2 раздела 3): рост и расстояние от стопы до пупочной линии, расстояние от ключицы до локтя и от локтя до кончиков пальцев, длина указательного пальца и длина первых двух фалангов. Для эксперимента были взяты все учащиеся моего класса (9-го класса). Таким образом, 40% обследуемых учащихся подтвердили гармонию своего тела (смотрим приложение)
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
-
Детская энциклопедия по математике
-
Искатели необычайных автографов или странствия, приключения и беседы двух филоматиков; Эм. Александрова, В. Левшин; издательство «Детская литература» 1996г.
-
Очерки по истории математике; Б.В. Болгарский; Минск 1979 «Высшейшая школа»
-
Числа Фибоначчи; Н.Н. Воробьев; Москва «Наука» 1992; главная редакция физико-математической литературы
-
Информация из Интернет сети
ПРИЛОЖЕНИЕ
| Рост | Расстояние от стопы до пупочной линии | Отношение | Близость к золотому сечению |
| 167см | 98см | 0.59 | + |
| 170см | 97см | 0.57 |
|
| 176см | 99см | 0.56 |
|
| 164см | 94см | 0.57 |
|
| 168см | 96см | 0.57 |
|
| 160см | 89см | 0.56 |
|
| 169см | 100см | 0.59 | + |
| 177см | 105см | 0.59 | + |
| 162см | 90см | 0.56 |
|
| 171см | 99см | 0.58 | + |
40%
| Расстояние от ключицы до локтя | Расстояние от локтя до кончиков пальцев | Отношение | Близость к золотому сечению |
| 33см | 45см | 0.73 |
|
| 29см | 41см | 0.70 |
|
| 31см | 43см | 0.72 |
|
| 34см | 49см | 0.69 |
|
| 27см | 42см | 0.64 | + |
| 30см | 46см | 0.65 | + |
| 32см | 48см | 0.66 |
|
| 25см | 40см | 0.63 | + |
| 23см | 38см | 0.61 | + |
| 27см | 39см | 0.69 |
|
40%
| Длина указательного пальца | Длина первых двух фалангов | Отношение | Близость к золотому сечению |
| 8см | 5см | 0.63 | + |
| 10см | 6см | 0.6 | + |
| 9см | 6см | 0.67 |
|
| 7.9см | 5.5см | 0.7 |
|
| 9.2см | 6.4см | 0.7 |
|
| 8.5см | 4.5см | 0.53 |
|
| 9.8см | 6.1см | 0.62 | + |
| 8.7см | 6см | 0.7 |
|
| 8.9см | 5.7см | 0.64 | + |
| 9.4см | 6.2см | 0.66 |
|
40%

 Получите свидетельство
Получите свидетельство Вход
Вход












 Авторская разработка. Золотое сечение. Числа Фибоначчи (264.5 KB)
Авторская разработка. Золотое сечение. Числа Фибоначчи (264.5 KB)
 0
0 212
212 0
0 Нравится
0
Нравится
0







