Правило 1. Нельзя умножать или делить неравенство на выражение, не зная знака выражения.
Неправильно:
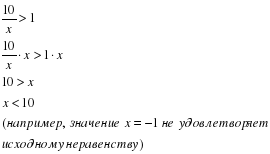
Правильно:

Вывод: умножать или делить обе части неравенства на x (или f(x)) можно только в том случае, если известен знак x (или f(x)).
Если x0 (или f(x)0), то при умножении или делении знак неравенства сохраняется.
Если xf(x)
В противном случае, когда знак x (или f(x)) не известен, следует переносить правую часть неравенства влево и решать методом интервалов.
Правило 2. Нельзя возводить неравенство в четную степень, не убедившись в том, что обе его части неотрицательны.
Неправильно:
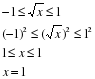

Очевидно, неравенство решено неверно.
Правильно:
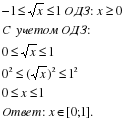
Вывод: возводить неравенство в четную степень можно только в том случае, если обе его части неотрицательны.
Правило 3. Нельзя переходить в неравенстве от функций к аргументам или от аргументов к функциям, не убедившись в монотонном возрастании (или убывании) функции.
Неправильно:
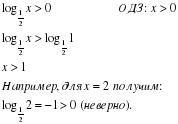
Правильно:
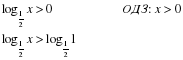
Так как a=0,5
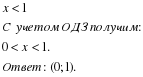
Вывод: при переходе от неравенства между функциями к неравенству между аргументами (или наоборот) следует учитывать вид монотонности функции.
Если функция монотонно возрастающая, то при переходе знак неравенства сохраняется.
Если функция монотонно убывающая, то при переходе знак неравенства меняется на противоположный.
В противном случае, когда вопрос о монотонности функции не может быть решен, переход в неравенстве от функций к аргументам и обратно невозможен.


 Получите свидетельство
Получите свидетельство Вход
Вход


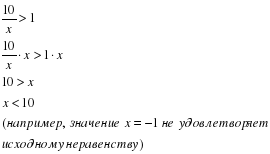

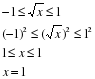

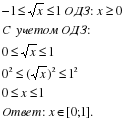
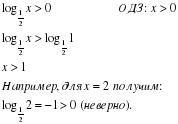
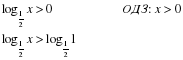
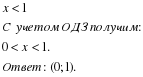









 Анализ типичных ошибок при решении неравенств (27.66 КB)
Анализ типичных ошибок при решении неравенств (27.66 КB)
 0
0 1555
1555 98
98 Нравится
0
Нравится
0


